実務で使える金融工学　実践編

１.　QuantLibを使ってみる

1.2　Exampleを試す

1.2.2 EquityOption: シンプルな株式オプションの価格計算

最初に紹介するExampleとして、“EquityOption”を選びました。イントロダクションで説明した通り、QuantLibを端的に説明すると、「Financial Instruments」というキャッシュフローの情報を格納しているオブジェクトに、「Pricing Engine」という価格計算のアルゴリズムを格納しているオブジェクトを組み合わせた、金融商品の価格計算ライブラリです（リスク量の計算など、その周辺の機能も含まれます）。その仕組みが最も解りやすい例がこのテストプログラムかと思います。この２つの中心となるオブジェクトは、それぞれ必要な部品を組み立てて作ります。その部品自体もさらに細かなパーツを使って組み立てます。そういった様子がこのExampleのソースコードを見ればよく解ると思います。 

1.2.2.1 ソースコードのコンパイルと実行

まず Example のソースコードをビルドし、実行可能なバイナリーファイルを生成します。QuantLibのインストール方法のセクションで、既にビルドしていれば、再ビルドは必要ありません。もし、ビルドが済んでいない場合は、次の手順で、Debugモードでビルドし、試しに実行してみて下さい。 

1. QuantLibのフォルダー下にある"Examples"フォルダーから、"EquityOption"のディレクトリを探し、そこにある"EquityOption.vcxproj"をダブルクリックして下さい。Visual Studio が起動され、このプロジェクトファイルが開かれます。
2. Visual Studioの画面中にある"ソリューションエクスプローラー"に表示される"プロジェクトファイル"のディレクトリを展開し、"SourceFiles"のフォルダーにある"EquityOption.cpp"をクリックします。約４００行あるソースコードが開かれます。
3. きちんと動作するか、まず確認してみましょう。メニューバーからビルド→ソリューションの“ビルド”を選択。ビルドが開始されます。既にビルド済みであれば、このステップは必要ありません（当初、複数のプロジェクトをまとめているQuantLib.slnをビルドした場合、個別のプロジェクトにおけるmain()関数を走らせる必要があります。その場合は、ソリューションエクスプローラーwindowから、該当のプロジェクト（ここではEquityOption.）をクリックした上で、メニューバーから “プロジェクト”　→　“スタートアッププロジェクトに設定”　を選択して下さい。）li>
4. エラー無くビルドが正常終了すれば、試しにプログラムを走らせてみます。メニューバーのデバック→デバックの開始を選択。下記のConsole画面が出力されれば成功です。（但し、プログラムが終了すると同時にConsole画面も消えてしまう様であれば、メニューバーから、ツール→オプション→デバック→全般とし、「デバックの停止時に自動的にコンソールを閉じる」 のチェックボックスをはずします。）
5. このConsole画面を見れば判る通り、このExampleでは、シンプルな株式オプションを、３種類の行使タイプに分けて、それぞれの価格を、１７種類の価格計算エンジンを使って算出しています。

1.2.2.2 ソースコードの解析

< 全体像 >

まず、ソースコードの全体像を把握しておきましょう。（参考のために、ソースコード(EquityOption.cpp ファイル）を .html ファイルに変換したものを、用意したので、それを見ながら読み進めて下さい。）
  冒頭に説明した通り、QuantLibの中心機能は、

• 価格計算の対象となる”金融商品のオブジェクト”（"Instrument"クラスのインスタンス）と、実際の計算を行う”価格エンジンオブジェクト”（"PricingEngine"クラスのインスタンス）を生成し、
• この２つを結合させ（"PricingEngine"を"Instrument"に設定して）、
• Instrumentクラスのメンバー関数であるNPV( )メソッドを呼び出して価格計算を行います。

このExampleのソースコードも、その流れに沿って書かれています。そして、InstrumentオブジェクトもPricingEngineオブジェクトも、それぞれ主要な部品を組み立てて生成されます。 

"Instrument"を構成する主要な部品は、その商品の Cash Flow を特定する為の様々な情報です。このExampleで使われている、Equity Option であれば、オプション行使日（"Exercise"オブジェクト）とPayoff関数（"Payoff"オブジェクト）の情報です。オプションの"PricingEngine"を構成する主要な部品は、キャッシュフローの発生確率を特定する"Stochastic Process"オブジェクトとDiscount Factorを計算する"TermStructure"オブジェクト（リスクフリー金利のイールドカーブ）です。 

このExampleでは、具体的な商品として、シンプルな株式のプットオプションを、Instrumentの派生クラスである"VanillaOption"クラスを使って、３種類生成しています。すなわち、この商品の主要部品である"Exercise"オブジェクトとして、ヨーロピアン、バーミューダン、アメリカンの３種類の部品を用意し、それらを使って３種類のVanillaOptionインスタンスを生成しています。さらに、"PricingEngine"を１７種類用意しています。これらを組みあわせて、様々な商品に対し、様々なアルゴリズムを使って、価格計算を行っています。 

これを念頭に、"EquityOption.cpp"のソースコードの中身を見ていきましょう。最初の例なので、できるだけ丁寧にコードの説明をしたいと思います。 

まず、プログラミングコードの全体像を見てみましょう。EquityOption.cppは約400行ありますが、最初から132行目までは、"Instrument"と"PricingEngine"の主要部品を生成しています。そして、それらの部品を使って、135行目から137行目で、"Instrument"の派生クラスである"VanillaOption"のインスタンスを３種類生成しています。 

VanillaOption europeanOption(payoff, europeanExercise);
  VanillaOption bermudanOption(payoff, bermudanExercise);
  VanillaOption americanOption(payoff, americanExercise);  

部品の作成に、相当のステップ数を使いましたが、部品さえできてしまえば、Instrumentオブジェクトの生成は、たったこれだけです。 

141行目以降は、様々な"PricingEngine"を生成して、それを使って３種類の"VanillaOption"の価格計算を行っています。具体的には、VanillaOptionインスタンスにPricingEngineインスタンスを設定し、NPV()メソッドを呼び出して価格計算を行い、結果をConsole画面に出力しています。 

< ステップ毎の説明 >

全体像を把握した上で、ステップ毎にソースコードを見ていきましょう。 

①　例外処理 

55行目からmain( )関数がスタートしますが、その直後から、最後の return　0; まで、try{…}で囲んでいます。そうすると、{…}内で何らかのエラーが発生すれば、例外処理に飛ぶようになっています。ここでは標準テンプレートライブラリーが提供しているエラーメッセージが出力されるようになっています（413と416行目）。QuantLibにも、Errorクラスという、エラーメッセージをオブジェクト化したクラスがありますが、このExampleでは使われていません。 

②　Boost::timerの起動 

59行目でboostライブラリのtimerが起動されています。timerは、main()関数が起動されてから returnで終了するまでにかかる時間を計測しています。timerインスタンスを生成した時点でストップウォッチがスタートし、return の直前でストップウォッチを止め、経過時間を出力します。先ほどの Console出力画面の最後の行を見ると、すべての計算に33秒かかっています（計算時間はPCの性能や計算時の環境に依存します）。Console画面に計算結果が出力されていく様子を注意深く見ると、計算時間の大半は一番最後のMonteCarlo(Longstaff Schwartz)というPricing Engineを使った、アメリカンオプションの価格計算にかかったものです。本来、Monte Carloシミュレーションは、アメリカンオプションの価格計算には不向きですが、Longstaff-Schwartzにより紹介された、最小2乗Monte Carlo法を使えば、無理やり価格計算できなくもありません。但し、計算時間は相当かかるので、他に方法が無い場合に限って使うべきでしょう。 

③　Global Settings：　グローバル変数の設定

64から66行目で、今日の日付と、決済日をそれぞれ1998年5月15日と、5月17日に設定しています。ずいぶん古い日付で、おそらくQuantLibの開発プロジェクトが始まった頃に作られたExampleだと推察します。66行目は、Settingsクラスのインスタンスを生成し、そのメンバー変数である　evaluationDate　（時価評価基準日）に、’本日’(＝1989年5月15日)のデータを設定しています。Settingsクラスは、プロジェクト全体で使われるグローバル変数を格納するオブジェクトです。このクラスは、Singletonクラスの派生クラスで、デザインパターンのひとつSingletonパターンの技法を使って設計されています。このクラスの解説は飛ばします。Luigi Ballabio氏の著作”Implementing QuantLib”に詳しいので、そちらをご覧下さい。

④　部品の生成

さて、ここから、価格計算に必要な、２つのメインのオブジェクト"Instrument"と"PricingEngine"を生成していきますが、その前に、まずその部品を生成する所から始めます。

④-1　カレンダー

少し前後しますが、63行目でCalendarインスタンスをTARGET()を使って生成しています。"Calendar"オブジェクトは、キャッシュフロー日が営業日である事を確認する為に必須であり、InstrumentクラスやPricingEngineクラスの部品となります。TARGETとはTrans-European Automated Real-time Gross-settlement Express Transfer システムの事で、European Central Bankが管轄している即時グロス決済の資金決済システムの事です。EU加盟国は多数あり、それぞれの国の休日にあわせて決済システムを止めてしまうと休日だらけになってしいます。そこで、逆にEU加盟国の営業日の最小公倍数的なカレンダーを作って、どこかの国が営業日なら資金決済システムを開けておくようにしています。このTARGETシステムをベースにしたCalendarを"TARGET"と呼んでいます。このExampleでは便宜的にTARGETインスタンスを使っていますが、実際には商品の取引市場や、取引当事者の所在国などを基準に決められます。
  QuantLibでは40か国程度のCalendarクラスが定義されています。国をまたぐ取引では、複数の国のCalendarが適用になる事が多いので、その為のクラスも用意されています。 

④-2　オプションの条件 

69から90行目は、オプションの価格計算に必要な入力項目を設定しています。Black-Scholes-Mertonのオプション価格公式で使われている入力項目とほぼ同じです。これらの項目は、オプションという“商品の属性”として取引当事者間で決めたものと、価格計算の際に使われる“市場データ"や"パラメータ”が混在しています。行使価格（strike）やオプション期日(maturity)は商品の属性で、"Instrument(商品オブジェクト)"の部品になります。それ以外は市場データで、"PricingEngine(価格エンジンオブジェクト)"の部品になります。但し、この段階では部品を生成する為の原材料を準備しているだけです。78行目以降は、これらの情報をConsole画面に出力するためのコードです。 

100行目から112行目までは、オプションの主要部品である、"Exercise"オブジェクトを３種類生成しています。 EuropeanExercise、AmericanExercise、BermudanExerciseはそれぞれ"Exercise"クラスの派生クラスで、名前の通り、「行使日」をオブジェクトモデル化したものです。ここでは、Boostライブラリが提供するスマートポインタのひとつshared_ptrを使って、それぞれのインスタンスへのポインターを生成しています。スマートポインタとは、メモリー上にあるポインターが指し示す変数領域の生成・消去を自動的に行ってくれるポインターの事です。 

④-3　市場データ 

114から127行目は、市場データを格納する部品を生成しています。即ち、’対象資産（Underlying）の市場価格’、’リスクフリー金利’、’配当利回り’、および　’Volatility’です。 

対象資産の市場価格ですが、70行目で作成済のunderlying変数に格納されています。しかし、これは部品を生成する為の原材料にすぎません。114行目で、それを使って"SimpleQuote"オブジェクトへのスマートポインタを生成し、それを"Handle"オブジェクトに格納しています。"SimpleQuote"が部品で、それを保持する"Handle"は、部品を"PricingEngine"に繫ぐソケットのような役割りです。

<市場データ　と　"Quote"オブジェクト、"Handle"オブジェクト > 

QuantLibでは基本的に、市場データを、"Quote"オブジェクトに格納して使います。ここで使った "SimpleQuote" は"Quote"オブジェクトの派生クラスです。また、その"Quote"オブジェクトを、直接Pricing Engineに渡すのではなく、一旦"Handle"オブジェクトに保持させて、それをソケットのように使ってPricing Engineにデータを渡しています。ここで、コードの解析から少しはずれて、なぜこのような設計方法を取っているかについて、簡単に解説します。 

QuantLibは、巨大な価格計算モデルライブラリですが、それを単独で使うのでは無く、何等かのポジション管理システムやリスク管理システムの中に組み込んで使われる事を想定しています。そのようなシステムは通常、外部の市場データシステム（ロイターやBloombergなど）と接続され、そこから、常に更新される市場データを受け取っています。市場データが動けば金融商品の価格も変わるので、動いた都度、InstrumentオブジェクトあるいはPricingEngineオブジェクトに知らせ、必要があれば価格を再計算する仕組みが必要です。人間が、市場価格をモニターしながら、価格が動いた都度、それをPricing Engineに手入力して再計算するようでは、とても間に合いません。 

QuantLibでは、デザインパターンのひとつであるObserverパターンを使い、市場価格の変動を、InstrumentやPricing Engineが常にモニターし、必要に応じて価格の再計算を行える仕組みを備えています。それを実現する手段として、コード中にある"SimpleQuote"クラスを使っています。このクラスはObservableクラスの派生クラスで、それに対し、"Instrument"や"PricingEngine"オブジェクトはObserverクラスの派生クラスになっています。"Observable"は、市場データを格納し、データの更新が行われた都度、それを"Observer"へ通知する機能を備えています。一方"Observer"は、名前の通り"Observable"を常に監視(Observe)しており、データ更新の通知を受取ると、必要に応じて再計算などの動作を起動します。 

さらに、"SimpleQuote"オブジェクトを直接Pricing Engineに渡さず、一旦"Handle"オブジェクトに保持させて、その"Handle"をPricing Engineに渡しています。その理由は、複数の’情報源’に対応する為です。例えば、日経２２５の先物は、大証（東証と合併して日本取引所になっています）に上場されていますが、同様の商品がSIMEX（Singapore International Monetary Exchange）にも上場されています。SIMEXは大証がクローズした後でもオープンしており、大証クローズ後は、SIMEXのデータを使って価格計算を行いたいと考えるのは自然な事です。Handleクラスは、実質的にはポインターに対するポインターになりますが、機能としては、部品を価格エンジンに取り付けるソケットの役割りを果たします。すなわちHandleクラスの保持しているSimpleQuoteオブジェクトを、必要に応じて簡単に、別のSimpleQuoteオブジェクトに付け替える事が出来ます。「簡単に」の意味は、ポインターを付け替える際に必要なメモリーの生成・消去の管理を、自動的に行ってくれるという意味です。 

要するに、常に動いている市場価格への対応と、複数の情報源への対応のために、このような仕組みが取られています。より詳細な説明は、Luigi Ballabio氏の“Implementing QuantLib”を参考にして下さい。 

話が大分それましたので、元に戻します。 

'リスクフリー金利'と、'配当利回り'も、既に、ローカル変数　riskFreeRate と dividendYield に格納されています。この段階では部品ではなく原料です。先ほどと同様、これを使って、"YieldTermStructure"オブジェクトを生成します。このオブジェクトもObservableの派生クラスであり、先ほど説明した仕組みを取り入れています。さらに、そのポインターを"Handle"オブジェクトに格納して、それをPricingEngineに渡します。回りくどい仕組みを取った理由は先ほどのSimpleQuoteと同じです。 

さらに’Volatility'も既に、変数volatilityに格納されています。先ほどと同様に、これを使って"BlackVolTermStructure"オブジェクトを生成しています。これもObservableの派生クラスです。そして、そのポインタを"Handle"に格納しています。 

これで、市場データの部品が揃いました。実は、これらの部品は、Pricing Engineの直接の部品ではなく、確率過程をオブジェクトモデル化した"Stochastic Process"オブジェクトの部品になります。そして、その"StochasticProcess"がPricing Engineの部品になります。 

④-4　Payoff 

さて、128と129行目ですが、"VanillaOption"のもうひとつの重要部品である"Payoff"オブジェクトを生成しています。ここでは、最もシンプルなPayoff関数を提供する"PlainVanillaPayoff"クラスのインスタンスを生成しています。このオブジェクトは、コンストラクターに、オプションのタイプ（Putか Call）　と　ストライク価格　を渡して生成されます。いずれの情報も、すでに'type'と、'strike'という名前のローカル変数に格納されており、これを使って生成されています。 

④-5　Stochastic Process（確率過程）オブジェクト 

130から132行目は、確率過程を記述した"BlackScholesMertonProcess"オブジェクトを生成しています。このクラスは、"StochasticProcess"クラスの派生クラスです。“基礎編”のオプションの所で、オプションの価格は期待値であり、対象証券の価格の確率過程がわかれば、どんなオプションであっても、かならず価格が求まると述べました。従って、このオブジェクトは、Payofffと共に、OptionのPricing Engineにとって、必須の部品になります。参考のために、QuantLibのリファレンスマニュアルから抜粋したこのクラスの派生関係のチャートを添付します。ここで使われている確率過程クラス以外にも、様々なクラスが用意されている事が分かります。 

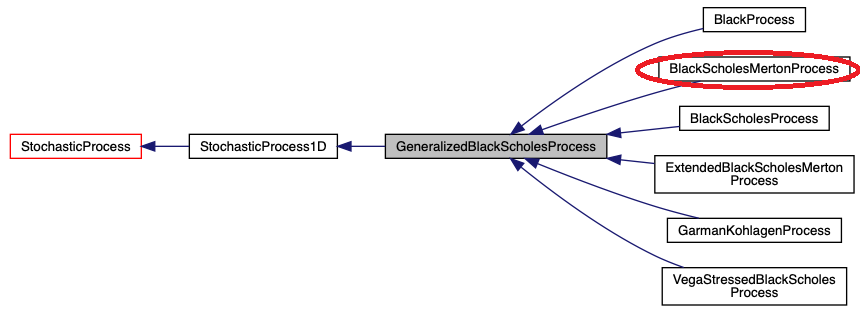
このオブジェクトが、Pricing Engineの直接の部品になります。そのコンストラクターに、先ほど作った市場データの部品を渡して、具体的なインスタンスを生成しています。 

ext::shared_ptr bsmProcess(new BlackScholesMertonProcess(underlyingH, flatDividendTS,
                                         flatTermStructure, flatVolTS));

このExampleでは、１７種類のPricing Engineを使って、３種類のオプションの価格計算を行っていますが、Heston ModelとBates Modelを使ったPricing Engine以外は、すべてここで生成されたBlackScholesMertonProcessを使っています。このクラスは、具体的には、リスクフリー金利から配当利回りを引いた割合相当のドリフト項を持ち、一定のVolatilityで幾何ブラウン運動をする、株式の確率過程をオブジェクトモデル化したものです。 

 

以上で必要な部品の準備は終わりました。いよいよこれらの部品を使って"Instrument"と"PricingEngine"を組み立てます。 

⑤　"Instrument" オブジェクトの生成  

QuantLibの中で価格計算の対象となっている商品はすべて、"Instrument"ベースクラスの派生クラスです。ここでは、そのひとつ、"VanillaOption"クラスを使って具体的な商品を生成しています。"VanillaOption"オブジェクトの主要部品は、すでに作成されたPayoffとExerciseオブジェクトです。 

ソースコードの135,136,137行目でそれぞれ、ヨーロピアン、バーミューダン、アメリカンの行使条件をもつ"Vanilla Option"を生成しています。引数として、部品となるPayoffとExerciseのインスタンスを渡しているのがわかります。部品の構築には相当ステップ数をかけていますが、部品が揃ってしまえば、商品オブジェクト生成は簡単です。但し、QuantLibを使いこなそうと思えば、どういった金融商品が、どのような部品で出来ているのか、さらにその部品が、さらにどのようなパーツから出来ているか、を理解する必要があります。他のExampleの説明も参考にしながら、その辺りの感覚をつかんで頂ければと思います。 

⑥　"PricingEngine"オブジェクトの生成と価格計算 

さて、商品オブジェクトが出来上がったので、次は"PricingEngine"の生成です。あとは、それを商品オブジェクトに設定すれば、価格計算が出来ます。このExampleでは17種類のPricing Engineを生成し、それぞれのエンジンを使った計算結果をConsole画面に出力しています。 

Pricing Engineは大きく分けて、解析解を使ったものと、数値解を使ったものに分けられます。さらに後者は、数値積分を使ったもの、有限差分法を使ったもの、２項Treeを使ったもの、そしてMonte Carloシミュレーション法を使ったものに分けられます。各Pricing Engineで、計算方法は大きく異なりますが、やっている事の本質は、(i)"StochasticProcess"から導出される確率分布をもとに、(ii)"Payoff"関数の期待値を計算し、(iii)その現在価値を求める事です。失礼しました。有限差分法だけは、一般的な期待値計算方法とは、かなり異なった方法で期待値を導出しています。それについては、ここで解説しませんが、上級編”寄り道：期待値の導出方法”で簡単に解説しています。 

⑥-1　解析解による価格計算 

142から150行目は、かの有名なBlack-Scholes-Mertonが導出したヨーロピアンオプションの価格公式を使って価格計算を行っています。この価格式は、Black-Scholes-Merton過程を記述した確率偏微分方程式を解析的に解いていって導出された解析解です。 

下記コードにある通り、Pricing Engineの「生成」と「商品への設定」という２つの動作を、setPricingEngine( )メソッドの呼び出しの中で同時に行っています。ここで使われている価格エンジンは"AnalyticEuropeanEngine"です。 

europeanOption.setPricingEngine(boost::shared_ptr(
                                     new AnalyticEuropeanEngine(bsmProcess)));

部品の準備には、ずいぶん手間がかかりましたが、オブジェクトの組み立てと設定は、たったこれだけです。Pricing Engineのコンストラクターに、部品としてStochasticProcessオブジェクトしか渡されていません。Discount Factorを計算する部品、すなわちリスクフリー金利のイールドカーブは必要ないのでしょうか？当然必要です。AnalyticEuropeanEngineクラスのコンストラクターは、Stochastic Processオブジェクトだけを引数で取るタイプと、それに加えてTermStructure（イールドカーブ）オブジェクトも引数として取り込むものと、２種類用意されています。前者の場合は、StochasticProcessの部品構築に使われたイールドカーブを、Discount Factorを計算する目的にも使っています。Stochastic Processオブジェクトを生成する際、その部品の中にリスクフリー金利のTermStructureインスタンスが含まれていた事を思い出して下さい。後者は、Stochastic Processのドリフト項を計算する為のイールドカーブと、Discount Factorを計算する為のイールドカーブが異なる場合に使います。 

これで価格計算の準備はすべて終了です。　あとはInstrumentオブジェクトが持つNPV()メソッドを呼び出せば、価格計算が実行され結果が返ってきます。147行目にある
europeanOption.NPV()
という記述がそれです。 

⑥-2　Stochastic ProcessとしてHeston Modelを使った解析解  

153から167行目までは、Heston Modelを使ったPricing Engineの生成と計算結果の出力です。Heston Modelとは、Black-Scholesモデルでは定数として取り扱われていた拡散項の係数（すなわちvolatility）を、それ自体も確率変動するものと仮定した確率過程のモデルです。この種のモデルを総称してStochastic Volatilityモデルと呼んでいます。このモデルは、実際の市場で観測される分布の歪みを取り込む為に仮定されたものです。

ここでは、"HestonProcess"というStochastic Processオブジェクトをまず作ります。そのオブジェクトの部品は既に作られているので、それらを使ってコンストラクターを呼び出すだけです。Hestonモデルでは、Volatilityの初期値以外にもいくつかのパラメータを特定する必要がありますが、この例では、とりあえず外生的にコンストラクターに与えています。ここでは、モデルの詳細や計算アルゴリズムには立ち入りません。かなり難解な数学のテクニック（フーリエ変換を使った期待値演算など）を使ってオプション価格を導出しており、相当ページを割かないと説明しきれません。解析解と言ってますが、数値積分を使っているので、完全な解析解とは言い切れません。Exampleでも"Semi-Analytic"とタイトルが付いてます。計算結果はConsole画面に出力された通り、Black-Scholesモデルによる解析解とほぼ一致しています。というより、一致するようにHeston Modelのパラメータを調整した結果と思われます。 

⑥-3　Stochastic ProcessとしてBates Modelを使った解析解 

170から184行目までは、Batesモデルを使ったPricing Engineの生成と計算結果の出力です。BatesモデルはHeston ModelにJump Diffusionの項を加えたものです。Jump Diffusionとは、確率変数が連続的に変化するだけではなく、ときおりジャンプを起こすももと想定した確率過程です。ここでもモデルの詳細には、立ち入りませんが、計算結果はBlack-Scholesモデルのそれとほぼ一致しています。（これも、一致するようにCalibrationした結果と思われます。） 

⑥-4　アメリカンオプション価格を解析的近似解で求める方法 

187から206行目までは、アメリカンオプションの解析的近似解を導出した２つの価格モデルを使ったものです。ひとつは、Barone-Adesi-Whaleyモデルで、もうひとつはBjerksund-Stensland モデルです。Pricing Engineのアルゴリズムの詳細には立ち入りませんが、通常、アメリカンオプションの価格計算は2項・3項Treeを使った数値解か、有限差分法を使った数値解を使うのが、一般的です。しかし解析的に価格が求まれば、計算時間は大幅に短縮できます。Console画面に出力された計算結果の通り、数値解のPricing Engineで計算した値と、若干ずれが発生しています。実務で使うのであれば、よりポピュラーな数値解の方法を使った方がいいと思います。 

⑥-5　数値積分によるオプションの価格計算 

209から217行目は数値積分法を使った数値解による価格計算を行っています。"IntegralEngine"のコンストラクターにbsmProcessオブジェクトを渡し、Pricing Engineを生成し、NPV()を呼び出して価格計算を行っています。やはり、価格モデルのアルゴリズムの詳細には立ち入りませんが、計算結果は、Black-Scholesモデルの解析解とほぼ一致しています。数値積分によるオプション価格計算は、\( \sum Payoff \times \ Probability \times \ Discount Factor\ \) という期待値計算の式を、まさにその通りに計算しており、最も理解しやすいオプション価格計算方法かと思います。 

⑥-6　有限差分法を使ったオプションの価格計算 

220から236行目までは、有限差分法（Finite Difference Method）を使った価格計算です。有限差分法は、２項Treeやモンテカルロシミュレーションと比べると、アルゴリズムがかなり複雑で、プログラムコードを理解するには、数値解析や行列演算に関する一定レベルの知識が必要です。しかし、計算の収束速度や、Greeksの計算、複雑なデリバティブズへの対応力などは、他の数値計算と比べると一段秀でていると思います。 

ここでは、３種類の商品オブジェクト、すなわちヨーロピアンオプション、バーミューダンオプション、アメリカンオプションの各商品に対応する、Pricing Engineを３種類用意し、価格計算を行っています。それぞれ、
FDEuropeanEngine
FDBermudanEngine
FDAmericanEngine
というテンプレートクラスを使ったPricing Engineです。 

有限差分法によるオプション価格の計算アルゴリズムについては、それだけで一冊の本ができるくらいで、とてもここでは説明しきれません。参考までに、下記文献を紹介しておきます。 

Daniel Duffy, “Finite Difference Methods in Financial Engineering” John Wiley & Sons Ltd.
  Luigi Ballabio, “Implementing QuantLib”- Chapter VIII- Finite Difference Framework  

⑥-7　２項モデルによるオプションの価格計算 

239から345行目までは、２項Treeモデルを使った7種類のPricing Engineを使ってオプション価格を計算しています。金融工学の書籍等で一番みかけるのは、２番目のCox-Ross-Rubinsteinの２項Treeモデルではないかと思います。これらのモデルの違いについては、下記インタネットサイトに簡潔な解説があります。 

Goddard Consulting

また、２項Treeモデルによる価格計算のアルゴリズムをQuantLibライブラリの中でどのように設計しているかについては、Luigi Ballabio氏の “Implementing QuantLib”- Chapter VII- The Tree Framework“　を参考にして下さい。 

各モデルの計算結果をみればわかる通り、いずれもBlack-Scholesの解析解にほぼ一致しています。Black-Scholesの価格公式はヨーロピアンオプションについてしか使えませんが、ここでテストされている２項Treeモデルはすべて、バーミューダオプションやアメリカンオプションにも対応できます。。 

２項モデルは、一般的に数値解を求める手法の中では計算時間が早い方で、かつエキゾチックオプションへの対応範囲も広いのが特徴です。一方で、Greeksの計算では、離散時間の間隔が広すぎると不正確になります　実務で使うにはTreeのメッシュを相当細かくする必要があり、それに伴い、計算時間も長くなります。 

⑥-8　モンテカルロシミュレーションによるオプションの価格計算 

348から396行目までは、モンテカルロシミュレーション法を使ったPricing Engineです。ここでは、３種類のPricing Engineを生成しています。 

最初のPricing Engineは、コメントにMC　（Crude）とあるように、最もシンプルなモンテカルロシミュレーション法を使ったものです。具体的には、コンピューターのアルゴリズムを使ってPsuedo-Random（疑似乱数）を発生させ、それを使って対象証券価格の拡散過程をシミュレーションし、最後に期待値計算をします。簡単に言いましたが、そのステップは何段階にも分かれており、相当複雑です。Exampleのコードからは、裏で走っているアルゴリズムが分からないので、それも含め少し詳しく説明します。

• まず、事前準備です。348と350行目にtimeSteps=1, mcSeed=42と設定しています。Time Stepが１の意味は、確率過程の中途を飛ばし、現時点から、一気にオプション期日の株価をシミュレーションするものです。ヨーロピアンオプションであれば、途中の価格過程の情報は必要ないからです。またmcSeedは、乱数生成アルゴリズムに渡すシード数です。
• 352行目で、MCEuropeanEngine<、PseudoRandam>というモンテカルロシミュレーション価格エンジンを生成しています。MakeMCEuropeanEngine (bsmProcess) というメソッドを使って、Pricing Engineを生成しています。.withXXX(...)という形で必要な部品を追加していますが、この手法はFactoryパターンと呼ば出るデザインパターンの手法です。
• 356行目で、このPricing Engineを、商品にセットしています。そして　360行目で、この商品のNPV()メソッドを呼び出して価格計算を行っています。このNPV()を呼び出した瞬間に、以下のような、長いアルゴリズムが起動します。
  1. 一様乱数（0から1の間で、ランダムかつ均一に分布した小数の集合）の生成装置を組み立て、必要な数だけ一様乱数を発生させる
  2. 一様乱数を正規乱数に変換する
  3. StochasticProcessオブジェクト（ここではbsnProcessインスタンス）を使って、対象資産価格のオプション期日までのドリフト（平均）と、標準偏差を導出
  4. 正規乱数に、ドリフトと標準偏差を作用させ、オプション期日における対象資産価格のサンプルを必要数作る
  5. オプション行使日のPayofff関数を使って、各サンプルにおけるオプション行使価値を計算
  6. それを合算して、Paｔｈ数で割る。すなわち、Payofffの期待値を計算
  7. それにDiscount Factorをかけ、現在価値に換算する

コンピューターのアルゴリズムにより生成された乱数は、疑似乱数と呼ばれるくらいなので、完璧な乱数ではありません。

何をもって完璧な乱数と言うのかは、数学者の方にお任せします。詳しく分析すると、分布にどうしても何等かの偏りが出てしまうようです。分布の偏り以外にも、コンピューターのアルゴリズムからくる制約があります。まず、表現できる数字の数が、ビット数に依存します。64ビットであれば、最大 \(2^{64}\)　までです。さらに、アルゴリズムを使って乱数を生成するという性格上、同じシード数からスタートすると、同じ乱数列が生成されます。質の悪いアルゴリズムだと、その数列の途中に、すでに発生した乱数と同じ数が登場した場合、そこから循環して同じ乱数の列を生成してしまいます。実際に使われているアルゴリズムでは、この循環をうまく避けるよう工夫されています。

QuantLibでは、様々な疑似乱数の生成アルゴリズムを用意していますが、このPricing Engineでは、Mersenne Twisterと呼ばれるアルゴリズムが使われています。このアルゴリズムは、日本人の数学者の方が開発されました。 

２つめのPricing Engineは、乱数の発生装置にSobol のLow Discrepancy Sequence（低食い違い数列、あるいは超一様分布数列と訳されているようです）を使ったものです。Sobol列は、高次のモーメントが、純粋な乱数（数学者の方に怒られそうな表現ですみません）と一致するように、アルゴリズムを使って生成された乱数列です。ばらつき度合いの質が、疑似乱数より高い点と、数列を生成する為の計算時間が疑似乱数より短いという利点を持っています。一方で、生成される数列の数が、一定単位まとまらないとモーメントが純粋の乱数とマッチしないので、シミュレーションに使う乱数の数を、事前に決めておく必要があります。367行目で Size nSamples = 32768; // \(2^{15}\)   とサンプル数を最初に指定しているのは、その為です。

NPV()を走らせた後に起動するアルゴリズムは、一様乱数の生成の部分がSoboｌ列になっている以外は、MC（Crude）と同じです。 

３つめの価格エンジン、Monte Carlo (Longstaff Schwarts)は、モンテカルロシミュレーション法を使って、アメリカンオプションの価格計算を行っています。既に触れましたが、このPricing Engineの計算アルゴリズムは、Longstaff-Schwartzにより紹介された、最小2乗モンテカルロ法です。そのアルゴリズムの解説は省略しますが、計算時間が相当かかるので、他に方法が無い場合にのみ使うべきでしょう。 

< まとめ　>

以上、様々なPricing Engineオブジェクトを使ったオプション価格計算法を紹介しました。繰り返しますが、QuantLibはデリバティブズの価格計算の為のライブラリーです。その大きな枠組みは、 

• キャッシュフローの情報を提供するFinancial Instrumentのオブジェクトを生成
• 価格計算のアルゴリズムをカプセル化したPricing Engineオブジェクトを生成
• それらを結合させて、NPV()というメソッドを呼び出し、価格計算を実行し、結果を返すというものです。

この２つのオブジェクトを構成する様々な部品もまた、オブジェクト化されクラスライブラリーとして用意されています。こういった部品を組み合わせる事によって、様々な金融商品オブジェクトと、その価格を計算するPricing Engineを組み立てる事ができます。それらの部品の組み立て方をマスターすれば、QuantLibを使いこなせるようになったと言えるでしょう。解ったように言っていますが、膨大なライブラリなので、私自身も使い方をすべてマスターしている訳ではなく、勉強中です。 

 

<ライセンス表示>

QuantLibのソースコードを使う場合は、ライセンス表示とDisclaimerの表示が義務付けられているので、添付します。   ライセンス