基礎編 4. オプション
4.2 オプションのデルタヘッジ戦略
オプションモデルが数学的にどのように導出されるかを理解するには、オプションのデルタヘッジ戦略を理解する事が不可欠です。
まず、それについて解説したいと思います。具体的な取引を使って、丁寧に説明したいと思います。その結果、ヘッジ戦略から生まれる損益がどうなるのか、見てみたいと思います。
オプション価格式の導出過程をきちんと理解している人や、金融機関でオプションのトレーディングを経験している人には当たり前の結果です。しかし、金融オプションの勉強を始めたばかりの人には、ちょっとした発見になるかも知れません。
4.2.1 事例:トヨタ株を使ったオプション取引
< トヨタ株の株価推移 >
トヨタの株を例に使います。
2017年11月から2018年2月15日のトヨタの株価推移は、下記のようなものでした。
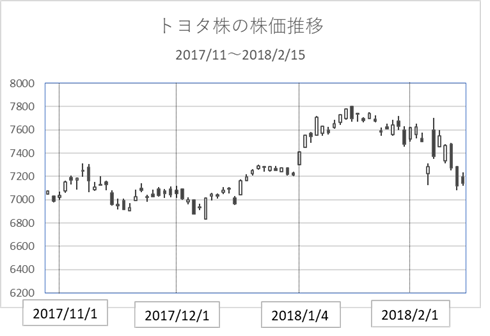
この株価の終値の日々の"変化率"について、この期間の平均と標準偏差を計算すると、以下のようになりました。
| %変化率 | 対数変化率 | |
| ドリフト係数(平均) | 0.050% | 0.043% |
| 拡散係数(標準偏差) | 1.1711% | 1.1714% |
| 拡散係数(年率換算) | 18.52% | 18.52% |
このデータが示すのは、トヨタの株価は、この3か月間、1日平均0.05%上昇し、毎日おおむね1.17%程度変化していたという事です。拡散係数を年率換算していますが、日々の変化率に \(\sqrt{250}\) を掛けているだけです。250 は大体1 年間の営業日の日数で、実務ではこれに近い数字を使うのが一般的です。営業日日数は国によって異なりますが、金利の計算の時のように厳密な日数計算を行う必要ありません。なぜなら、この数字は、期間を意味するのでは無く、株価の変動を離散的に捉える際の、1年間の観測回数と見做せるからです。観測回数を、例えば前場と後場の終値で1日2回観測し、その間の変化率を計算した場合、1年間の観測回数は約500回になります。半日の株価変化率の標準偏差を約500個のデータから求め、それに\(\sqrt{500}\) を掛けたのが年率換算になります。逆に、週に1回しか観測しないで、それを年率換算する場合は、\(\sqrt{52}\) を掛けます。1日1回の観測で計測された拡散係数すなわちVolatilityは、Daily Volatility、週1回の観測で計測された拡散係数はWeekly Volatilityと呼ばれています。
< トヨタ株を対象とするオプション取引 >
トヨタほどの規模の会社になると、株の流動性が高く、また世界中の機関投資家が注目している株なので、個別株のオプションも頻繁に取引されていると思われます。(データが無いので推定で言ってます。しかし、もしあなたが機関投資家で、大手の投資銀行のトレーディングデスクに電話してトヨタのオプションを取引したいと言えば、少なくとも価格の呈示はしてくれると思います。)
上記データによると、トヨタの株価は2月15日時点で7142円でした。その日、そのトレーディングデスクに、ある機関投資家から、行使日が6カ月後で行使価格が7800円のヨーロピアンコールオプションを10万株売りたいとオファーがありました。その投資家は、おそらくトヨタの株は6カ月後でも7800円までは上昇しないであろうと予想しているのかも知れません。あるいは、既にトヨタ株を10万株以上持っていて、6カ月後に7800円を越えるようなら、そこで売却してもいいと考えているのかも知れません。
行使日までの期間がそれほど長くない、シンプルなヨーロピアンコールオプションなので、Black-Scholes-Mertonの公式を使ってオプション価格を計算するのが一般的です。(行使日までの期間が長く、金利の影響が大きくなると、別の価格計算方法を考えた方がいいと思います。) 価格公式に代入する必要がある、オプションの条件や市場データは次の通りであったと仮定します。
- 現時点(2月15日)の株価: 7142円
- オプションタイプ: ヨーロピアンコールオプション
- 行使価格(Strike Price): 7800円 (約9.2% Out of the Money)
- 行使日: 8月15日(約6カ月)
- リスクフリー金利: 1.0%
- 配当利回り: 2%
- 借株料: 0.5%
- Volatility: ?
Volatilityだけ“?”としているのは、ほかの数値はすべて客観的に求まりますが、Volatilityは、そうとは限りません。この数字はトヨタ株の将来の変動率の予想になるので、人によって見方が異なります。この値をどのように決めればいいでしょうか? 仮に、トヨタのオプションが市場で頻繁に取引されているようなら、そこから客観的に求まります。すなわち、その値は、市場が予想している将来のトヨタ株のVolatilityになります。しかし、個別株のオプションの場合、価格が公表されているケースは稀です。では、どのようにすればいいでしょうか?
そういった場合、トヨタ株の過去のVolatilityが参考になります。過去のVolatilityと全く同じ値で将来も変動するとは限りませんが、そこから大きく離れないと推定するのも不自然ではありません。そこでトヨタ株の過去3か月のDaily Volatilityを見てみると、約18.5%でした。仮にこの値を使ってオプション価格を計算すると1株あたり約130円になります。トレーダーとしては、この価格をそのまま呈示すると利益が上がらないので、一定のマージンを取った上で価格呈示します。このケースでは30円のマージンを取って、1株あたり100円(株価に対する比率では1.4%)のBid価格でそのオプションを投資家から買う事にしました。
Black-Scholes-Mertonモデルを使って、オプション価格が100円になるようなVolatilityは、16.6%でした。逆に言えば、上記の条件にVolatility16.6%を使ってBlack-Scholes-Merton公式に代入すると、ヨーロピアンコールオプションの価格は100円となります。このようなVolatilityの値を、Implied Volatilityと呼びます。オプション価格が内包しているVolatilityの水準という意味で、予想Volatilityとも呼ばれます。このケースでは、トレーダーは向こう6カ月のトヨタ株のDaily Volatilityは16.6%を下回らないであろうと予想していたと言えます。
Black-Scholes-Merton公式に入力する市場データの中に、観測されたトヨタ株のHistorical Dateによる平均値(ドリフト)は、一切使われることはありません。参考にされる事もありません。この公式の導出の中で、確率過程のドリフト項は消え、結果的にリスクフリー金利に置き換わるからです。
ここで、Black-Scholes-Mertonのヨーロピアンオプションの価格公式を下記しておきます。この式の導出過程は別の所で解説します。とりあえず所与のもの(given)として考えて下さい。以下、この式を使って、オプション価格やデルタを計算します。
\[ CallPrice_{BSM-model}(S,K,T,Rfr,Dr,Br,Vol)=e^{-(Dr+Br)T}\times S\times N(d_1) - e^{-Rfr\ T}\times K\times N(d_2) \hspace{20mm} \\ d_1=\frac{\ln(S⁄K)+(Rfr-Div-Br+Vol^2⁄2)T}{Vol\sqrt{T}} \hspace{52mm}\\ d_2=\frac{\ln(S⁄K)+(Rfr-Div-Br-Vol^2⁄2)T}{Vol\sqrt{T}}=d_1-Vol\sqrt{T} \hspace{30mm} \\ \]但し
- S: Spot Price(現在の株価)
- K: Strike Price(行使価格)
- T: Term (オプション行使日までの期間、単位;年)
- Rfr: Risk Free Rate(リスクフリー金利、連続複利ベースの年率表示)
- Dr: Dividend Rate (配当利回り、連続複利ベースの年率表示)
- Br: Stock Borrowing Rate(借株料率、連続複利ベースの年率表示)
- Vol: Volatility(拡散係数またはボラティリティー、年率表示)
- N( ): 標準正規分布関数
当初のBlack-Scholesの公式では、配当利回りや借株料率の変数は含まれていませんでした。Mertonがこれを若干改良して、配当支払いがある株について、配当利回りを変数として加えました。さらに、実務では借株料率を変数に加えるのが一般的です。デルタヘッジ戦略を取るには、株のショートポジションを作る必要があり、その為には株を借りてそれを市場で売却します。株はタダでは貸してくれないので、それにかかるコストも、きちんとモデルのパラメータとして取り込む必要があるからです。但し、借株料率の取扱いは、配当利回りと全く同じであり、上記式中でも同じ位置にあることが見て取れます。
(注) 少し話がそれますが、配当利回りを、上記の式のように、あたかも毎日発生する“金利”のように取り扱うのは問題があります。実際に配当が支払われるのは、配当の受取権が発生する“権利日”の所有者にだけです。株価はそれを勘案して、権利日の翌日には予想配当額に相当する割合で下落します。いわゆる配当落ちです。上記のような配当利回り方式でオプション価格を計算すると、権利日の前後でオプション価格がジャンプしてしまいます。それを調整しようとすると、権利落ち日の前後で配当利回りを大きく動かす必要があります。そうすると、ヘッジ比率が大きく動くなど、また別の問題が発生します。配当支払いを、離散的なCash Flowとして取り扱うオプション価格計算方法がいくつか提示されており、実務ではそちらを使うべきかと思います。ここでは、デルタヘッジ戦略を理解するのが目的なので、上記の式をそのまま使います。
借株料率については、毎日発生する金利のように取り扱って全く問題ありません。実際にそうだからです。
ちなみに、借株料率と配当利回りを、外国通貨のリスクフリー金利に置き換えれば、為替のヨーロピアンオプションの価格式になります。