上級編 5. マルコフ汎関数モデル
5.2 Markov Functional Model(マルコフ汎関数モデル)
5.2.1 モデルの概要
Markov Functional Model(マルコフ汎関数モデル、以下“MFM”)は、将来のゼロクーポン債価格(すなわちイールドカーブ)、さらにはそれを対象にしたデリバティブズ価格を、マルコフ過程を取る確率変数の確率(遷移)密度関数を使って、ニュメレールとの相対価格の期待値として求めます。”はじめに”でも触れた通り、マルコフ汎関数モデルは、“モデル”というより、金融商品の期待値(すなわち価格)計算のフレームワークと考えるべきでしょう。その基本的な考え方は、
- 1個から数個の状態変数となる確率変数と、その確率密度関数が解析的に特定できる確率過程(一般的には低次元のマルコフ過程)を仮定し、
- ニュメレール価格を、その確率変数の(汎)関数として定義し、(但し、必ずしもその関数形を特定する訳ではありません。従って、関数というより、写像とか対応関係(Mapping)と言った方がいいでしょう。その点については後述します)
- その確率分布を、CAPやSwaptionの市場価格に内包されているフォワード金利の確率分布を使って導出し、
- さらにそれを使って、任意の満期のゼロクーポン債価格(すなわちイールドカーブ)を、ニュメレールとの相対価格の期待値演算(汎関数)で求め、
- さらに、そのイールドカーブの変動に依存する金利デリバティブズの価格を求める。
というものです。一般的な価格モデルのように、価格評価の対象となる金融商品の確率過程を考えるのではなく、相対価格計算に使うニュメレールの確率分布を使うという点と、そのニュメレールの確率分布を市場データからInterpolation-Bootstrappingと似たようなアルゴリズムで求める点で、その他のオプションモデルとは全く異なるアプローチをとっています。
そして、ニュメレールとしては、デリバティブズの価格評価に必要なDiscount Factorとして一番期間の長いもの(すなわち、最長期のゼロクーポン債)を選択します。
以下、Hunt-Kennedy-Pelsser の論文(“Markov Functional Interest Rate Models”)をベースに、MFM のフレームワークについて、解説したいと思います。
5.2.2 状態変数の確率過程
まず、上記の 1. ですが、確率変数となる状態変数 x は、ガウス分布するマルコフ過程を取ると仮定します。
\[ dx(t)=σ(t)dW(t),~~~~~x(0)=x_0=0 \tag{5.2} \]Volatility係数については、金利の中心回帰傾向を取り込むため、
\[ dx(t)=σ~e^{at}dW(t),~~~~~x(0)=x_0= 0 \tag{5.3} \]という関数形で定義する事も可能です。こうする事により、フォワード金利の Intertemporal Correlation (時系列相関)のコントロールが可能になります。但し、その分、Calibration のアルゴリズムが複雑になりますが。(Short Rate Modelの所でも、この中心回帰パラメータの Calibration が簡単では無い旨述べました。)
\(dW(t)\) については、低次元すなわち 1 から数個のブラウン運動を仮定しますが、実務では1ファクターを使うのが一般的です。2ファクター以上になると、Calibration の計算時間が非常に長くなったり、収束しないケースが増えたりして、非常に扱いにくくなる為です。
5.2 式、5.3 式とも、ドリフト項を 0 としています。また拡散項にある \(dW(t)\)は、ニュメレールに対応する測度下で変動するブラウン運動になります。従って、x はニュメレール測度下でマルチンゲールとなるガウス分布(正規分布)する確率変数と仮定されています。
この状態変数(確率変数)xの役割は、その他のオプションモデルにおける確率変数の役割と少し異なります。Black-Scholes モデルや、Short Rate Model 群、あるいは Libor Market Model 群のいずれも、確率変数として、金利や金融商品の価格を選択し、それが拡散していく様子を、確率微分方程式の形でモデル化しています。確率変数の一定期間後の確率分布は、そのモデルを時間で積分する事で導出されます。モデルが Hull-White モデルのように、通常のブラウン運動により瞬間短期金利が拡散されていく場合(ガウス過程)、一定期間後の分布はガウス分布(正規分布)になります。また、Black-Scholes モデルや Libor Market Model では、株価やフォワード金利が幾何ブラウン運動しながら拡散していくと仮定しており、そこから一定期間後の株価の分布は対数正規分布となります。さらに、Local Volatility モデル や Stochastic Volatility モデルのように、あえて将来の確率分布を(対数)正規分布からずらそうとするモデルもありますが、それらについても、金利や価格の一定期間後の確率分布は、(導出方法はかなり複雑ですが)理屈としてはモデルを積分する形で導出されます。
しかし、MFMでは、ゼロクーポン債価格をこの状態変数の汎関数(写像)と見做すものの、その将来の確率分布を、5.2 式や 5.3 式を積分するのではなく、全く別の方法で求めます。x はゼロクーポン債価格が拡散していく様子を記述するものの、一定期間後のゼロクーポン債価格の確率分布は、x の分布からではなく、それとは直接関係しない市場データから求めます。何を言ってるんだ?と思いますよね。これをどう理解すればいいのでしょうか?
x の役割は、実際には(対数)正規分布からずれたニュメレールの分布を、正規分布する座標にマッピングする為に、その座標軸を提供していると理解すればいいでしょう。試験の評価でよく使う偏差値と似たような役割です。仮に x が -2 であれば(偏差値でいえば 30 に相当しますが)、x に対応するゼロクーポン債価格は、予想される価格分布の中で、下から 2.3% の位置にある事を示しています。x が、5.2式や5.3式の形で、拡散過程を取るのは、ニュメレールの相対位置(偏差値)がそのような過程を取り、一定時間後の偏差値の分布が正規分布になるという風に理解すればいいでしょう。試験を繰り返した場合、偏差値が遷移していく分布が正規分布すると判っており、さらに各試験の得点の分布(正規分布からはずれていますが)が判っていれば、今回の試験で偏差値が 30 だった人の、次回の試験での得点の期待値を求める事は可能です。MFMにおける、ガウス分布する状態変数 x の役割は、こういうものと理解すればいいでしょう。
5.2.3 ニュメレール価格を x の汎関数(写像)として定義
t 時における、最長期 \(T_n\) 満期のゼロクーポン債価格、すなわちニュメレール価格は、正規分布する x の汎関数(写像)として、下記のように定義されます。
\[ N(t,T_n)~∶=~N(t,T_n,x_t) \]但し、先ほども述べましたが、他のオプションモデルと異なり、この関数(写像)形は、5.2 式や5.3 式を解析(積分)して導出される訳ではありません。
この関数形を、パラメトリックな関数として特定する事も可能ですが、MFM を紹介した Hunt-Kennedy-Pelsser の論文では、関数形を特定していません。関数形を特定しないで、x とニュメレール価格の対応関係(写像)を定義しているだけです。
(注 : MFM をパラメトリックなモデルと、非パラメトリックなモデルに分けて説明している文献もあります。パラメトリックなモデルについても、パラメータを市場価格にフィットさせやすいような関数形を、無理やり外生的に与える(仮定する)もので、5.2 式 や 5.3 式を解析(積分)して導出した関数形ではありません。状態変数 x の役割はあくまで座標軸の提供です。ここでは、ノンパラメトリックなMFMのみ解説します。)
まず、ニュメレールの価格が変化していく様子を簡単に見てみます。ゼロクーポン債の価格は、満期が近づくにつれ価格1(元本の100%)に収束していきます。仮に、現時点から満期まで、金利が変動しないと仮定すると、次のような価格カーブを描くでしょう。
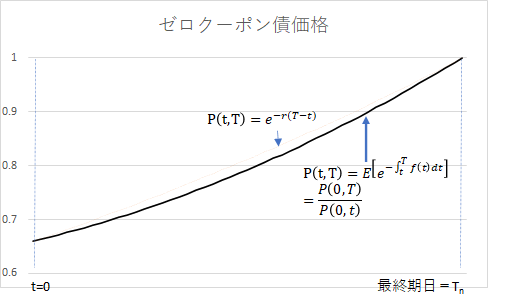
上側の線は、ニュメレールとなるゼロクーポン債利回りが一定とした場合の価格。下側の線は、現時点のイールドカーブが内包するフォワード金利をベースに、予想される価格の期待値の推移を示しています。ニュメレール価格は、この下側の線に沿って分布していると予想されます。グラフにすると、下記のようなイメージです。帆船の例でいえば、曲線が航路で、点がそこからのずれになります。
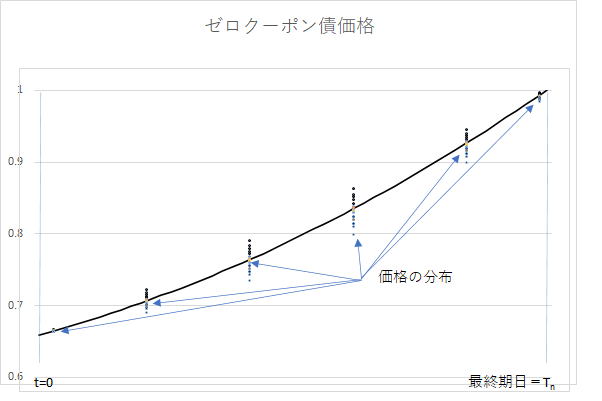
ニュメレール価格の確率分布として求めたいのは、まさにこの分布がどうなっているかという事です。ゼロクーポン債価格は、時間の経過とともに拡散していくものの、満期に近づくと、価格が1に収束するので、価格の絶対値でみた分散の度合いは小さくなります。しかし、各時点のニュメレールの最終利回りの分布でみれば、時間の経過とともに、拡散していく様子が見て取れます。下記のようなイメージです。
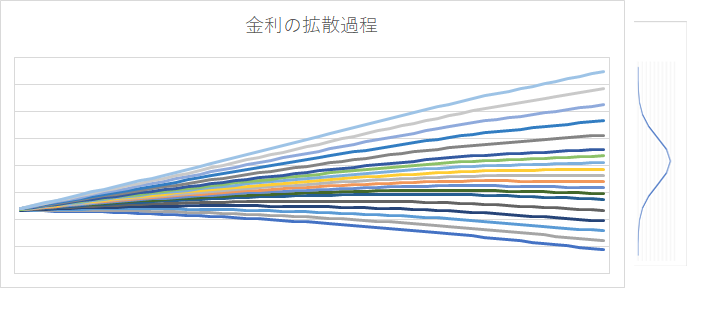
ニュメレールの価格の分布は、まさにこのフォワード金利の確率分布から求めていきます。すなわち、CAP や Swaption の市場価格に内包しているフォワード金利の確率分布から、ゼロクーポン債価格の確率分布を導出し、それを正規分布する状態変数 x にマッピングします。市場価格に内包されているフォワード金利の確率分布は、いわゆる Volatility Smile の形状を持ち、(対数)正規分布からずれています。従って、そこから導出されるゼロクーポン債価格の分布もずれたものになります。ニュメレール価格の汎関数 \(N(t,,T_n,x_t)\) は、それを正規分布する x への対応関係を示す写像になります。x の役割が偏差値と同じようなものという意味がお判りいただけるでしょうか。
5.2.4 ゼロクーポン債価格の汎関数を求める。
ニュメレールと状態変数 x の対応関係(写像)が求まれば、任意の時点における任意の満期のゼロクーポン債価格(すなわちイールドカーブ)が、ニュメレールの相対価格の期待値(汎関数)として求まります。時間 t における状態変数の値が \(x_t\) で、その時のニュメレール価格が \(N(t,T_n,x_t)\) であったとします。その時、\(T_j\) 満期のゼロクーポン債価格は、\(N(t,T_n,x_t)\) に依存するので、これも \(x_t\) の汎関数とみなすことができ、下記のように表記します。
\[ P(t,T_j,x_t),~~~~t<~ T_j< ~T_n \]すると、そのニュメレールとの相対価格は、下記のような汎関数(条件付き期待値)で表現できます。
\[ \begin{align} \frac{P(t,T_j,x_t)}{N(t,T_j,x_t)} & =E^{Q_N} \left[ \frac{P(t,T_j,x_{T_j})}{N(t,T_j,x_{T_j})} ~|~x=x_t \right] \\ & =E^{Q_N} \left[ \frac{1}{N(T_j,T_n,x_{T_j})}~|~x=x_t \right],~~~~~~t~ < ~T_j~ < T_n \tag{5.4} \end{align} \]式から判る通り、t 時における \(T_j\) 満期のゼロクーポン債価格が、その満期時のニュメレール価格の確率分布から導出できるという事です。\(T_j ~ は~、\left[t,T_n\right]\) 間を離散的に区分した時間軸として設定されますが、適当な Interpolation を行えば、t 時における連続したイールドカーブが描けます。
イントロダクションで使った、帆船上のランニングマシンに乗せた動物の例でいえば、出帆後、到着前の任意の時点 t における帆船の位置(5.4 式の \(x_t\) に該当します)が判れば、その地点から、到着までの任意の時点 \(T_j\) における、帆船上の動物の位置が(要は、帆船の位置と同じですが)、条件付き期待値として求まり、その位置を繋げれば、ロサンゼルスまでの動物の位置の予測が出来ると言っているのと同じです。
5.2.5 デリバティブズ価格をニュメレールの相対価格の期待値として導出
t 時におけるイールドカーブが、上記のように、ニュメレールとの相対価格の条件付き期待値として求まるので、そのイールドカーブに依存する金利デリバティブズ価格も、ニュメレールとの相対価格の期待値として求まります。先ほどの 5.4 式で、t=0 すなわち現時点とし、右辺の期待値演算の中の分子を、ゼロクーポン価格ではなく、\(T_i\) 時(=行使日)のSwaptionのPayoff関数とします。(Capletは、キャッシュフローが 1 個のSwaptionと見做せるので、同じ式が使えます。)
\(T_i\) が行使日で、ストライクレートが K で、対象スワップの最終期日が \(T_n\) のヨーロピアン・(Payer)スワップションの価格を \(SwaptionPrice(0,K,T_i,T_n)\) と表記すると
\[ SwaptionPrice(0,K,T_i,T_n) = N(0,T_i,x_0) E^{Q_N} \left[ \frac{Annuity(T_i,T_i,T_n,x_{T_i}) (SwapRate(T_i,T_i,T_n,x_{T_i})-K)^+ }{N(T_i,T_n,x_{T_i})} ~|~ x_0 \right] \] \[ \begin{align} where~~ SwapRate(T_i,T_i ,T_n, x_{T_i}) & = \frac{(1-P(T_i,T_n,x_{T_i}))}{Annuity(T_i,T_i,T_n,x_{T_i})} \\ Annuity(T_i,T_i,T_n, x_{T_i}) & = ∑_{j=i+1}^n ~ \tau _j ~ P(T_i,T_j,x_{T_i}),~~~~\tau_j=T_j-T_{j-1} \tag{5.5} \end{align} \]但し
\(SwapRate(t,T_i,T_n,x_t)\) : t 時において、状態変数が \(x_t\) の時の、\(T_i\) スタート、\(T_n\) エンドのスワップ金利
\( Annuity(t,T_i,T_n,x_t)\) : t 時における、上記スワップの固定キャッシュフローに対応する Annuity 価格
この式の右辺の期待値演算の中にある、\(T_i\) 時のニュメレール価格、および分子にある Annuity() とスワップ金利 SwapRate() はすべて \(T_i\) 時(=オプション行使日)のゼロクーポン債価格から導出でき、さらに、そのゼロクーポン債価格はすべて、5.4 式の汎関数から導出できます。それらを使えば、右辺の期待値演算ができ、Swaption 価格を求める事ができます。また、Bermudan Swaption のように行使日が複数ある Swaption についても、ニュメレールの分布が時間軸に沿って離散的に求まっているので、Tree 構造を遡る要領で、価格を計算する事ができます。