上級編 6. Libor Market Model
6.2 古典的なLibor Market Model
6.2.5 Convexity Arbitrage (コンベクシティー アービトラージ)
私が、米国債やデリバティブズのトレーディングを行っていた 1990 年前後の事ですが、30 年物の米国債(いわゆる T-Bond)と、30 年満期のストリップ債を使ったスプレッド取引が盛んでした。ストリップ債は、80 年代半ばに登場したばかりの商品でしたが、瞬く間に市場が拡大し、非常に流動性が高い人気の商品になりました。ストリップ債の価格は、米国債のイールドカーブから、理論上は一意に決まりますが、ストリップ債は、満期日により人気の差(需給の差)が大きく、理論値からかなりずれる傾向にありました。
当時でも今でも、30 年物の T-Bond の利回りと、30 年物のストリップ債の利回りの変化には、強い相関があります。当時(90年代前半)の T-Bond の利回りは、5~8%程度でしたが、イールドカーブがノーマルであれば、30 年物のストリップ債の利回りは、それよりも高くなります。また、ストリップ債は満期までキャッシュフローが発生せず、個人投資家にとって節税のメリットがあります。さらに、ストリップ債は、Convexity (利回りー価格 曲線の曲率)が非常に強い商品で、同じリスク量(Basis point sensitivityが同じ)であれば、T-Bond よりもイールドの変化に対し、上下方向どちらにも有利な価格変化をします。これらの理由から、30 年満期のストリップ債は人気が高く、しばしばイールドカーブから導出される理論値よりも高い値段(低い利回り)で取引されていました。ちなみに、Convexity は、債券の価格式を金利 r で 2 階微分したもので、債券の利回りー価格曲線の曲率にあたります。満期が T で利回りが r のゼロクーポン債の価格式は \(e^{-rT}\) で、これを r で 2 階微分すると \(T^2 e^{-rT}\) となり、通常の金利環境であれば、T が大きくなるにつれ、Convexityが大きくなります。(注: \(T\) が大きくなると \(T^2\) は増大するものの、\(e^{-rT}\) は指数関数的に減衰します。しかし通常の金利環境ではTが相当大きくならないと、指数関数的な減衰効果はあらわれません)
この T-Bond とストリップ債との Convexity の差をグラフで表すと下のようになります。
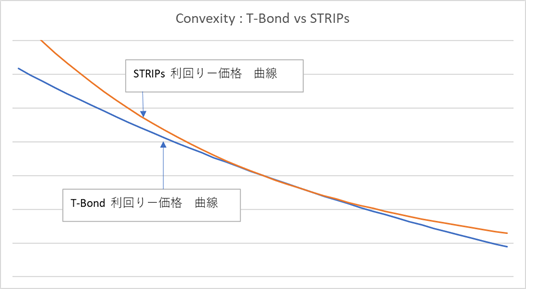
注 : このグラフは横軸が利回りで、縦軸が価格になります。但し、価格軸は、T-Bond と STRIPs 債を比較可能にする為、それぞれ現時点の価格を 1 として正規化し、さらに Basis Point Sensitivity を同じにして(すなわち同じリスク量で)比較しています。
グラフを見れば判る通り、金利が上昇すると(グラフの横軸で右方向に進むと)価格は低下しますが、その低下の度合いは、T-Bond の方が強くなります。また、金利が低下すると価格は上昇しますが、上昇の度合いは STRIPs 債の方が強くなります。すなわち、STRIPs 債の Convexity が、T-Bond の Convexity より強いという事です。
もし、T-Bond と 30 年物のストリップ債の利回り変化の相関が極めて高ければ、T-Bond をショートし、ストリップ債をロングにし、Basis point sensitivity が相殺されるようなポジションを組めば、そのポジションの金利に対する感応度は下記のような損益曲線になるはずです。
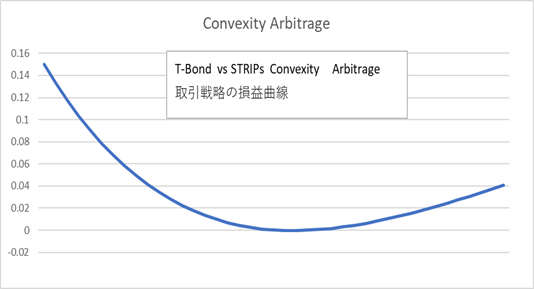
これは、オプションのロングポジションを、デルタヘッジでリスクを完全に消した場合と、同じ様な形です。この曲線の最小値の点(傾きが 0 の点)は、オプショントレーダーの言葉で言えば、デルタ・ニュートラルでガンマ・ロングのポジションになります。ぱっと見ただけでは、(本当はそうではないのですが)この取引戦略を組めば、オプションプレミアムを払う事なく、タダでオプションを手にいれたように見えます。ある人は、この取引をかっこつけて、Convexity アービトラージと呼んでいました。両者の相関が極めて高く 1 に相当近い場合、そのようなオプション価値は確かに存在します。しかし、市場がアービトラージフリーであれば、そのようなオプション価値は、既に価格に織り込まれているはずであり(STRIPs 債の価格が、オプション価値に見合うだけ高くなっており)、裁定機会は消えてしまっているという事になります。
実際のイールドカーブを観察しても、この Convexity の価値が STRIPs 債価格にどの程度織り込まれているか観測する事は出来ません。従って、Convexity アービトラージが可能かどうかを判断する基準は存在しません。
非常に極端な仮定として、金利の Volatility と相関が、イールドカーブ全領域に渡って、限りなく 0 に近かったとします。すると、Convexity から発生するオプション価値も 0 に近くなります。そういった状態でのイールドカーブを下記グラフの上の方とします。(現実には存在しない仮定のカーブです) それに対し、イールドカーブが、ある程度の Volatility で変動し、かつ相関も相当高いとすると、Convexity から発生するオプション価値が大きくなります。すると、アービトラージフリーであれば、価格にオプションプレミアムが乗っかり、価格が上昇します(利回りは低下)。それが、下のグラフの下側のカーブになります。上のカーブが観測できないので、今のイールドカーブに、Convexity 価値がどの程度織り込まれているか、計測できません。しかし、市場がアービトラージフリーという仮定は、観測されるカーブにそれが既に織り込まれていると仮定する事を意味します。
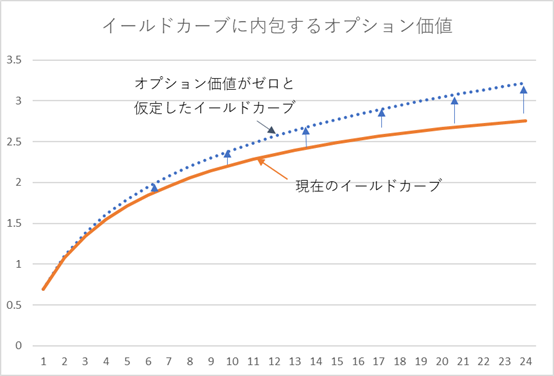
現在のイールドカーブも、時間の経過により期間の長いゾーンの残存期間が短くなってくると、Convexity は徐々に失われていきます。すると、理論的には、時間の経過と伴に、グラフの下のカーブと上のカーブの距離が、徐々に短くなります。
前のセクションで説明した、LMMのSDEに発生するドリフト項は、まさにこの、イールドカーブに織り込まれた Convexity の価値(オプション価値)が、時間の経過と伴に徐々に消えていく様子を表しています。6.33 式と 6.36 式のドリフト項の式をよく見れば分ると思いますが、その値は、ニュメレールの満期日と Libor のエンド日の距離(期間)、Libor 間の相関係数、各 Libor の Volatility、及び金利の絶対水準に比例します。それらの値が 0 に近づけば、Convexityの価値も 0 に近づきます。上のグラフで言えば、上側のカーブに接近していく事になります。実際に、今のような超低金利環境では、このConvexity価値はほとんどありません。
6.33 式にある通り、ニュメレールの期日に対し、Libor の期日が長い場合(\(T_i < T_k\) のケース)、SDE にプラスのドリフトが発生します。これは、Libor の Convexity がニュメレールの Convexity より強いためです(フォワード Libor は、スタート日とエンド日のゼロクーポン債を使って Replicate できるので、フォワード Libor を長期債のポジションと見做す事ができます)。市場がアービトラージフリーであれば、長期債の価格に Convexity 価値(オプション価値)が含まれて、若干高くなっているはず(従ってフォワード Libor 金利は低くなっているはず)です。その内包したオプション価値が、時間が経るにつれ徐々に失われていく(金利が徐々に上にドリフトしていく)のが、このドリフト項になります。だから、ドリフト項の係数がプラスなのです。
逆に、ニュメレールの期日が Libor の期日より長い場合は、ドリフト項でマイナス調整が発生します。3.36 式のドリフト項の符号がプラスマイナス逆になっているのは、その為です。
同様な Convexity の差は、金利先物と FRA との間でも存在します。3 か月物の金利先物は、その対象資産となる同じ期日の FRA と、ほぼ相関1で動きます。しかしながら、金利先物の決済は、取引所が定めた方法により、金利の上下に対する損益は完全な直線形(金利の変化幅 × 0.25)で行われ、なおかつ、決済は即時(翌営業日)です。すなわち金利先物の利回りー価格曲線は、Convexity がゼロです。一方、FRA では、金利の変化に対する価格変化は、決済日から現時点までの Discount Factor(ゼロクーポン債価格式は、金利の変化に対し下に凸の指数関数)をかけるので、Convexity が発生します。FRA のロングポジションを金利先物のショートでヘッジした取引戦略の損益は、上の STRIPs 債と T-Bond の Convexity アービトラージのグラフと同じような形です(曲率は、はるかに小さいですが)。しかし、市場がアービトラージフリーであれば、FRA のレートに Convexity 相当の価値が乗っかり(すなわちレートが低くなり)、金利先物が示すフォワード金利は、FRA のそれよりも高くなっているはずです。金利先物のレートを使ってイールドカーブを描く場合の Convexity 調整は、まさに、そのオプション価値を調整する為の操作になります。
先ほど、イールドカーブに含まれるオプション価値を示すグラフで、上側の点線のカーブは、あくまで仮定のカーブで観測できないと述べましたが、金利先物が取引されているゾーンでは、金利先物のレートをそのまま使って描かれるイールドカーブがまさに、上側のカーブに相当します。金利先物は Convexity がゼロなので、それを使って描かれるカーブは、全くオプション価値を持たないイールドカーブという事になります。
< 損失飛ばし取引 >
尚、T-Bond と 30 年物ストリップ債の Convexity アービトラージについては、後日譚があります。上記のように 30 年物ストリップ債は、税制上のメリットや、強い Convexity の為に、人気が高く、イールドカーブから導出される理論値よりも割高で取引されていました。ところが 90 年代の前半、それが異常なレベルまで買い進まれ、時には 30 年債の利回りを 20bp 以上も下回ることがありました。当時、イールドカーブの形状はノーマルだったので、これはかなり異常な水準です。そういった状態が何年か続いた後、今度は、ストリップ債が急激に売られ、スプレッドがプラスの水準に戻りました。その背景には、日本の投資家の特異な行動があったという話がありました。
というのは、当時、多くの日本の会社がバブルの崩壊により、株式投資や不動産投資で、バランスシートに巨額の含み損をかかえていました。その損失を実現させない為、多くの会社が米国債やデリバティブズ取引を使って、損失の先送り取引を行ったようです。時価会計が厳しくなる以前なので、そのような取引が可能だったのでしょう。つまり、市場価格が簿価を大きく下回り、巨額の含み損を抱えた投資有価証券(日本株や、日本株の特金ファンド)を、証券会社に簿価で買い取ってもらい、代わりに 30 年物のストリップ債を、市場価格より高い値段(おそらく額面相当額)で買う、入れ替え取引を行うのです。当時のストリップス債の市場価格は、金利がまだ高かった時代なので、額面の 15~20 % 程度であったと記憶しています。それを額面の 100% で買って、日本株の含み損を、ゼロクーポン債の含み損に置き換えるのです。ゼロクーポン債は、為替リスクはあるものの、30 年後には額面で償還されるので、30 年間、損失が表に出ず、尚且つ30年後には含み損が消えた事になります。
当時の、ストリップ債価格の異常値をみると、相当多数の会社が、巨額のストリップ債を購入したのではないかと疑っています。ストリップ債を Over-Par で買った会社があったとのジョークまで飛び交っていたほどです。ところが、こういった損失先送り取引(いわゆる、“飛ばし”取引であり、それにより山一証券が破綻したのは有名な話です)が、明るみに出て、金融当局やメディアから大きな批判を受ける事になります。すでに取り組んでいた、ストリップ債を使った“飛ばし”を解消する動きが起こり、その結果、異常な高値が解消され、今度は逆方向に激しく動きました。
ある証券会社で、ストリップ債の Convexity Arbitrage をしていたトレーダーは、その激しい動きに巻き込まれて巨額の損失を被り、その会社から解雇されたという噂話もありました。