1. QuantLibを使ってみる
1.2 Example を試す
1.2.7 Gaussian1dModels : Gaussian Short Rate Model と Markov Functional Model
1.2.7.2 Gaussian1dModels パート2
前回は、Gaussian1DModel の最初の約 300 行の解説をしました。そこでは、GSR モデル(Hull-White モデル)の Volatility パラメータを、Piecewise Constant な関数と見做し、ベンチマークとなるヨーロピアンオプションの Black Implied Volatility データに Calibration しました。そこでは、Calibration に必要な CalibrationHelper を、価格エンジンオブジェクトが自動的に生成してくれる事を説明しました。また、そこで生成された CalibrationHelper オブジェクトは、すべて At the Money のヨーロピアンスワップションでした。
今回は、Example コードの 294 行目以降について解説をすすめます。今度は、自動生成される CalibrationHelper が、価格評価しようとするバーミューダ・スワップションの条件に近くなるような方法を使います。
1.2.7.2.1 モデルパラメータのCalibration-(2)
(1) Calibration―(2)
294行目のstd::coutされるコメントをご覧下さい。上のコンソール画面出力でも確認できます。
“There is another mode to generate a calibration basket called MaturityStrikeByDeltaGamma. This means that the maturity, the strike and the nominal of the calibrating swaptions are obtained matching the NPV, first derivative and second derivative of the swap you will exercise into at each Bermudan call date. The derivatives are taken with respect to the model's state variable. Let's try this in our case.”
前に説明した通り、Gaussian1dNonstandardSwaptionEngine クラスは、価格エンジンの中で、CalibrationHelper オブジェクトを自動的に生成する機能を備えています。先ほどは、“Naive” と呼ばれる方法でした。ここでは、2つ目の“MaturityStrikebyDeltaGamma”と呼ばれている方法で、CalibrationHelper を生成します。この方法は、コメントにもある通り、自動的に生成されるヨーロピアンスワップションの、満期日、ストライク、みなし元本を調整して、それらの NPV、デルタ、ガンマが、バーミューダン・スワップションの各行使日における NPV、デルタ、ガンマに近くなるように生成するというものです。ここでは、バーミューダ・スワップションの対象スワップのみなし元本は1、ストライクは4%、満期日は 2024年5月なので、生成されたヨーロピアンスワップションの対象スワップも、それに近くなりました。実際に生成されたスワップションを見るのが解りやすいと思います。
304 行目で swaption オブジェクトから calibrationBasket() を呼び出しています。前のセクションで説明した通り、このメソッドは背後で PricingEngine に備わった CalibrationHelper の自動生成機能を呼び出しているのでした。今度は、“MaturityStrikebyDeltaGamma” モードで Calibration の対象となるヨーロピアンスワップションを自動生成しています。その結果生成されたリストは、309 行目の printBasket(basket) で呼び出され、コンソール画面に出力された通りです(下にその出力の部分を再掲します)。確かに、みなし元本は 1 近辺、ストライクは 4%、対象スワップの Maturity とオプション Expiry もバーミューダン・スワップションのそれと同じになっています。
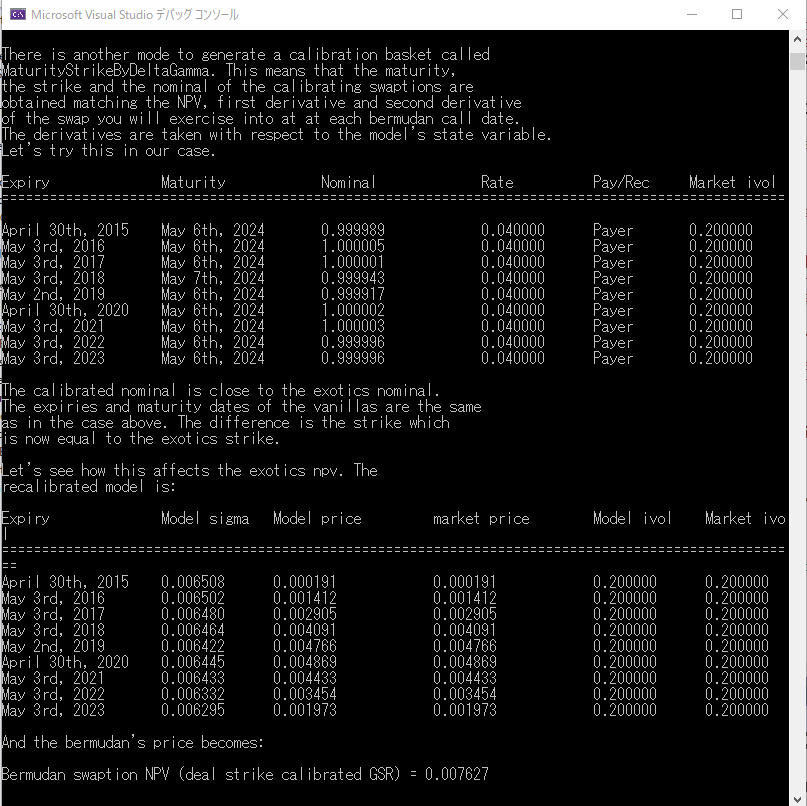
そして、今生成された CalibrationHelper を使って、Calibration を実行しています(312~325 行目)。すなわち、生成された CalibrationHelper に、それぞれ価格エンジンを設定し、GSR モデルから、calibrateVolatilitiesIterative( )メソッドを呼び出しています。
Calibration された結果は、上のコンソール画面出力にある通りです。Calibration 対象の市場データの数とパラメータの数が同じなので、ここでも、GSR モデルの価格と、ベンチマークモデルでの市場価格、及び Implied Black Volatility が完全に一致しました。しかし、CalibrationされたVolatility パラメータは、“Naive”モードの結果と比較して、大きくなっています。理由は、ご自分で考えてみてください。ヒントは、Black Volatility は、対数正規分布する確率変数の Volatility であるのに対し、GSR の確率変数は正規分布を仮定しています。
(2) バーミューダン・スワップションの価格計算
Calibration が終わったので、あとは商品オブジェクトから NPV() を呼び出して価格計算するだけです。334 行目の swaption->NPV( ) でそれが実行されました。上記のコンソール画面出力を見ると、計算結果は 0.007627(76.27bp)となりました。全く同じ条件のバーミューダン・スワップションを、同じ GSR モデルを使った同じ価格エンジンで計算したにもかかわらず、当初の計算結果 38.08bp の約2倍になっています。Calibration 対象のヨーロピアン・スワップションのストライクを変えただけで、かなり大きな違いが出ています。ここでは、Black Implied Volatility はストライクや満期に依存せず、すべてフラットと仮定しているので、この差は、Volatility Smile によるものではありません。この差は、先ほど説明した、対数正規 Volatility と正規 Volatility の違いから発生しています。
(3) モデルパラメータのCalibration-(3)
さらに、別の方法で Calibration 対象のヨーロピアンスワップションを生成し、それに Calibration する方法をテストします。342 行目のstd::coutによるコメントをご覧下さい。
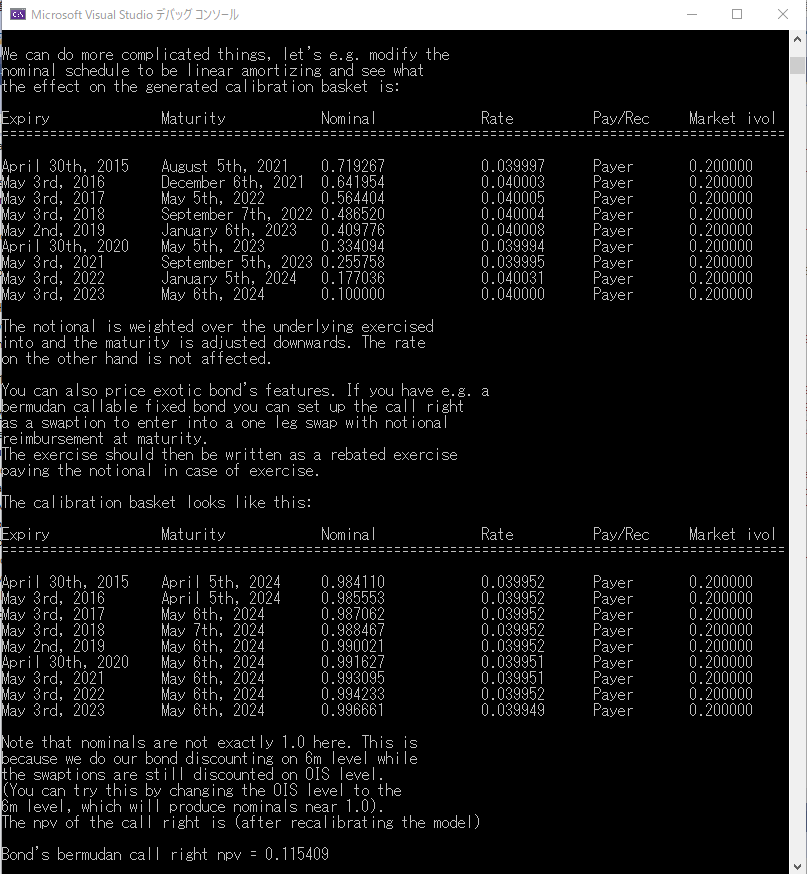
“We can do more complicated things, let's e.g. modify the nominal schedule to be linear amortizing and see what the effect on the generated calibration basket is …”
その意味は、この価格エンジンが持つ CalibrationHelper 生成の機能を使うと、みなし元本が逓減していくようなエキゾチックなバーミューダ・スワップションに対応した CalibrationHelper が生成できるという事です。元本が逓減していく債券は、減債条項(AmortizationあるいはSinking-Fund)付き債券と呼ばれ、債券市場では、時折見かける商品です。その債券にバーミューダタイプの Call Option が付けば、ここで価格評価しようとする、元本逓減型のバーミューダ・スワップションになります。
(3)-1 対象スワップの生成
まず、バーミューダ・スワップションの対象スワップ(元本逓減型)から作ります。348行目から355行目までで、みなし元本のキャッシュフローを、クーポン日に合わせて、逓減するように作っています。また、356行目で、行使日ごとにストライクレートの配列を生成しています。但し、すべて同じストライクレートです。これらの部品を使って、358行目で、新たにNonStandardSwapオブジェクト(underlying2インスタンス)を生成しています。
(3)-2 バーミューダ・スワップションの生成
対象スワップが出来たので、これを対象とするバーミューダ・スワップションのインスタンス swaption2 を 362 行目で生成しています。この Swaption に、先ほど生成した価格エンジン(nonstandardSwaptionEngine)を設定します(365行目)。そして、calibrationBaske( )メソッドを呼び出して、CalibrationHelper の配列を作っています(368行目)。結果は、下記のコンソール画面の出力をご覧下さい。これまでの2例とは、かなり異なるCalibrationHelperの配列が生成されています。すなわち、SwaptionHelperの満期日が、手前の行使日になるほど短くなっているのと、みなし元本も、対象スワップのみなし元本額に合うように調整されています。 なお、ここではCalibrationHelperの生成をテストしたのみで、このバーミューダ・スワップションの価格評価は行っていません。
(4) Callable Bond に内包している Call Option 価値の計算
(4)-1
380 行目にある std::cout のコメントをご覧下さい。今度は、これまでのバーミューダ・スワップションの価格計算方法を応用して、Callable Bond に内包されているバーミューダ・スワップションの価値を計算します。ここでは、Callable Bond を、バーミューダ・スワップションに似せて、その価値を計算しています。さらにこの例では、前の CallableBond の Example コードとは異なり、発行体のクレジットスプレッドを勘案して Call Option 価値を計算します。すなわち、債券の発行体が Call Option を行使するかどうかは、行使時におけるリスクフリー金利や、LIBOR-Swap カーブではなく、発行体の再調達コストを基準に判断されます。従って、行使するかしないかの境目、すなわち At the Money の金利水準は、リスクフリー金利カーブに発行体のクレジットスプレッドを加えたレベルが基準になります。これまでの例は、LIBORカーブが2.5%のフラットなカーブであったので、At the Moneyのレベルは、すべて2.5%でした。これを動かすと、どのようなCalibrationHelperが生成され、オプション価値がどうなるかテストしています。
(4)-2 バーミューダ・スワップションの対象スワップの生成
Call Option 付き債券は、スワップ(キャッシュフローの交換)ではないので、キャッシュフローは一方向の固定金利キャッシュフローと償還元本のみです。そこで、バーミューダ・スワップションの商品属性を少し加工して、Call Option 付き債券のそれに似せるようにして商品オブジェクトを作ります。
390 行目から 398 行目をご覧ください。まず、対象スワップにおいて、その固定金利CF のみなし元本を1(nominalFixed2)、変動金利CF のみなし元本を0(nominalFloating2)と設定します。394 行目で NonstandardSwap オブジェクトのコンストラクターに、この2種類のみなし元本を渡し、さらに、最終期日でのみなし元本交換フラッグ(コンストラクターの一番最後の引数)を“True(行う)”と設定すれば、固定金利債と同じキャッシュフローになります。このコンストラクターに渡す、キャッシュフロー期日やクーポンレートなどのその他の部品(引数)は、すでに作成済みのものを使います。また、発行体からみた Call Option は、行使するまでは固定金利を払い続け、行使すれば固定金利の支払いを免れるというキャッシュフローになるので、これまでのバーミューダン・スワップションのキャッシュフローと真逆になります。スワップタイプを Receiver スワップに変えているのはその為です。これで対象スワップが出来ました。(Exampleコードを見ただけでは、コンストラクターに渡している各引数が、それぞれ何を示すのかよく判らないと思います。QuantLib の Reference Manual で NonstandardSwap クラスのコンストラクターの引数を確認して下さい。)
(4)-3 バーミューダ・スワップションの生成
この一方向のキャッシュフローしかないスワップを対象資産とするバーミューダ・スワップションを作成します。400 行目で、スワップションの主要部品である Exercise オブジェクト(RebateEerciseクラスのオブジェクト)を生成していますが、コンストラクターに渡している2番目の引数(-1.0)がリベートになります。マイナスのリベートとなっているのは、オプションの保有者(すなわち発行体)が、オプションを行使した場合に元本償還義務、すなわち元本相当額のマイナスキャッシュフローが発生する為です。
(4)-4 価格エンジンの生成と、CalibrationHelperの生成
ここでは、発行体のクレジットスプレッドまで勘案した Call Option の価格を計算します。その為にまず、406~410 行目で、クレジットスプレッドを格納するオブジェクトを生成しています。ここでは 0bp と 100bp の 2 種類のスプレッドデータを用意しています。そして、このクレジットスプレッドも勘案した価格エンジンオブジェクトを生成します。即ち 412 行目で、Gaussian1DNonStandardSwaptionEngine クラスのインスタンスを生成していまが、引数として oas インスタンスを渡しています(oasはoption adjusted spread“オプション価値調整後のクレジットスプレッド”の略で、Call Option付き債券のクレジットスプレッドを表す業界用語としてよく使われます) これで価格エンジンの完成です。
価格エンジンが出来たので、これまでと同様にこれを使って、CalibrationHelper の配列を作ります。420 行目で、商品オブジェクトから calibrationBasket()メソッドを呼び出しています。生成された CalibrationHelper の配列は、コンソール画面の出力をご覧下さい。みなし元本と Strike レートが、それぞれ 1.0 と 4.0% から微妙にずれているのは、コメントにある通り、債券の Discount Curve は、LIBOR-Swap カーブを使っているのに対し、Swaption の Discount Curve は OIS カーブを使っている為です。
(4)-5 Call Option価格の計算(2通り)
商品と価格エンジンが出来たのであとは価格計算のみですが、その前に今生成された CalibrationHelper を使って、441 行目で、パラメータの Calibration を行います。そして、442 行目でswaption3-> NPV( )を呼び出して価格計算を行っています。計算結果は、上記コンソール画面の出力の通り、0.115409(11.5409%)となりました。これは、ストライクが 4% の、Receiverタイプのバーミューダン・スワップションの現在価値になりますが、クレジットスプレッド=0 の発行体の債券の Call Option と同じ経済価値になります。NPV が 11.5% と、これまでのバーミューダン・スワップションの評価と大きくずれているのは、スワップタイプを Receiver にしたからで、4% の行使価格は固定金利の Receiver にとっては Deep in the Money になっているからです。
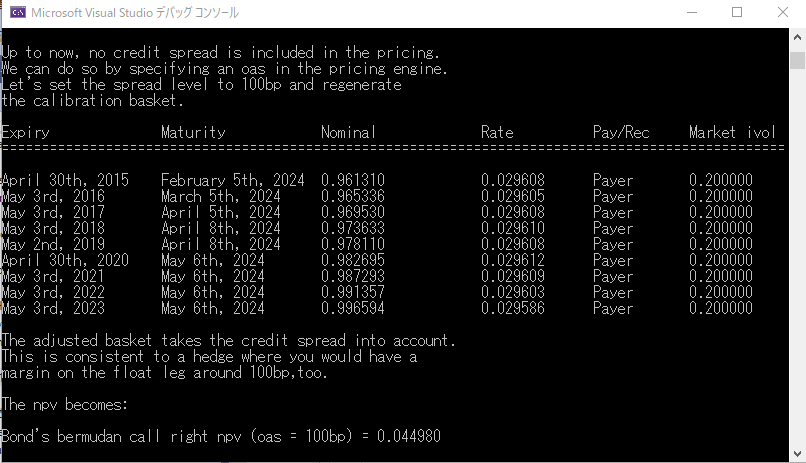
さらに 449 行目の std::cout のコメントをご覧下さい。今度は、クレジットスプレッドを 100bp として債券の Call Option 価値を計算します。455 行目の、oas.linkTo(oas100) で、Handle クラスのインスタンス oas に、oas100 という SimpleQuote のデータをリンクさせています。市場データを Handle オブジェクトに持たせ、それを価格エンジンに渡す手法は、“EquityOption”の所で説明済ですが、ここでもその仕組みを活用しています。そして、このデータをもとに、458 行目で改めて CalibrationHelper の配列を生成しています。その結果は、上記のコンソール画面の出力をご覧下さい。Calibration 対象として生成されたヨーロピアンスワップションのみなし元本が、おおむね 0.96~0.99 になっているのと、Strike レートがおおむね2.96% になっています。クレジットスプレッドを 100bp と想定しているので、Call Optionの保有者にとっては、保有するオプションのデルタやガンマが一致するのは、約3%のstrike金利水準のヨーロピアンオブションになるという事です。476 行目で再度モデルパラメータのCalibrationを行い、477 行目のSwaption ->NPV() で価格計算を行っています。計算結果は、コンソール画面の出力にある通り、0.04498=4.498%となりました。oas=0 に比べて価値が半分以下になりました。クレジットスプレッドが乗った為に、実質的な At the Money の水準が高くなり、In the Moneyの度合いが小さくなった為です。
<ライセンス表示>
QuantLibのソースコードを使う場合は、ライセンス表示とDisclaimerの表示が義務付けられているので、添付します。 ライセンス