実務で使える金融工学　上級編

上級編　６．　 Libor Market Model　

6.5  　Calibration

6.5.3    Calibration アルゴリズム

セクション 6.5.1 の“はじめに”で説明した通り、Calibration の対象となるベンチマーク商品として、Cap/Floor だけを考えるのか、Swaption まで含めるのかは、難しい問題です。Andersen-Piterbarg は、最小値問題の目的関数を工夫して、どちらの考え方にも柔軟に対応できる Calibration 方法を紹介しています。以下にそのプロセスを解説したいと思います。 

6.5.3.1　  Volatility 関数を Piecewise Constant なパラメータ行列とする。

LMM の Calibration アルゴリズムは、ベンチマーク商品の、"Black の公式"を使った市場価格（あるいは Black Volatility）と"LMM" を使ったモデル価格（あるいは、そこから導出される Implied Black Volatility）の誤差が出来るだけ小さくなるように、LMM の Volatility 関数のパラメータを調整する作業になります。　それらの差のノルム（価格誤差）を足し上げる目的関数を定義し、Solverを使って最適なパラメータ、すなわち「目的関数が最小値を取るようなパラメータの値」を導出します。Andersen-Piterbarg は、Volatility関数を、Piecewise Constant な行列と定義して、その各要素を Calibration されるパラメータとしました。 

Volatility 関数を Piecewise Constant な行列と定義する例は、すでに6.52式で示しました。それを再記します。 

\[ ϕ_i~ψ(t_j,T_i )=[{\bf G}]=\left[ \begin{array}{ccc} g_{1,1} & 0 & 0 \\ \vdots & \ddots & 0 \\ g_{n,1} & \dots & g_{n,m}\\ \end{array} \right] ~~~~ i=1,2,...,n~~~j=1,2,...,m \tag{6.52} \]

（但し、インデックス i は、フォワード Libor のインデックを示し、j は離散化した観測時間軸のインデックス。j=1 は \([0,T_0]\) の期間(すなわち現時点 \(t=0\) から、一番手前のLibor \(L_1\) の 金利 Fixing日である \(T_0\) までの期間)を示すインデックス。また\(j_m~は~T_{n-2}~から~T_{n-1}\)、すなわち最長期の Libor 金利 \(L_n\) の Fixing 日）までの期間を示すインデックス） 

ここで、ベンチマーク商品の Calibration で必要な情報は、6.39 式あるいは、6.48 式の右辺にある通り、拡散項係数のノルムの 2 乗です。そこで、Andersen-Piterbarg 本に倣い、\(ϕ_i~ψ(t_j,T_i)\) ではなく、\(‖ϕ_i~ψ(t_j,T_i)∙\bf C‖\) を Piecewise Constant な行列と見做します。こうしても、C が外生的に与えられるので、あとから \(ϕ_i~ψ(t_j,T_i)\) も簡単に導出できます。すなわち、 

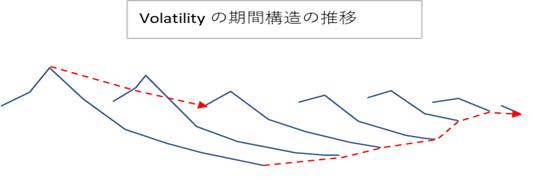
\[ \left[ \Vert ϕ_i~ψ(t_j,T_i) {\bf c_i} \Vert \right] =[{\bf G}]=\left[ \begin{array}{cccc} g_{1,1} & 0 & 0 & 0\\ \vdots & \ddots & 0 & 0\\ \vdots & \ddots & \ddots & 0\\ g_{n,1} & \dots & \dots & g_{n,m}\\ \end{array} \right] ~~~~ i=1,2,...,n~~~j=1,2,...,m \tag{6.73} \]

とします。こうすると、行列 G の各行は、各フォワード Libor \(Li\) の Piecewise Constant な（瞬間）Volatility になります。また各列は、観測時点 \(t_j\) における（瞬間）Volatility の期間構造になります。Volatility の期間構造の所で使ったグラフをもう一度下記しますが、実線部分が、各観測時点ごとの Volatility 期間構造になり（ G の列ベクトル）、点線部分が、特定の Libor の Volatility の時間経過による推移（ G の行ベクトル）になります。 

この Piecewise Constant な行列を使えば、Black Volatility と LMM の拡散項係数との関係式は、下記のように、積分形から Σ の計算に書き換えられます。 

<  Caplet の Black Volatility   >

\[ (BlackVol_(L_i ))^2 = \frac {1}{T_{i-1}} \int_0^{T_{i-1}} ‖ϕ_i~ψ(t,T_i)~~{\bf c_i}‖^2 dt =\frac {1}{T_{i-1}} \sum_{k=1}^{i-2} g_{i,k} \tag{6.74} \]

<   Swaption の Black Volatility  >

\[ \begin{align} (BlackVol_swap)^2 & ≈ \frac {1}{T_s} \sum_{i,j=s+1}^e \frac{ω_i (0)~ω_j (0)~L_i (0)~ L_j (0)}{Swaprate(0)^2} \int_0^{T_s} ρ_{i,j}(t)(ϕ_i ~ψ(t,T_i))(ϕ_j~ψ(t,T_j)) dt \\ & =\frac {1}{T_s} \sum_{i,j=s+1}^e \frac {ω_i(0)~ω_j(0)~L_i(0)~L_j(0)}{ Swaprate(0)^2 } \sum_{k=1}^{s-1} g_{i,k}~g_{j,k} \tag{6.75} \end{align} \]

ところで、観測時点 \(t_j\) の数は、モンテカルロシミュレーションを行う際の Time Step の数になりますが、最低でも、Libor のテナー構造の数が必要になります。確率変数となる Libor の数は、最大で 80～160 になるので、行列 G の次元は 80×80 とか、160×160 の規模が想定されます。この行列の要素をすべてパラメータとして使うと、明らかに Over-Fitting となるので、パラメータ行列としては、これをもっと簡略化した行列を使い、あとは線形補間により G を導出するようにします。そこで、その簡略化した行列を \(\bf \bar G \) と表記します。（行列の 4 つの角に入る値は、G と \(\bf \bar G \) で同じになりますが、\(\bf \bar G\) は G より、遥かに疎な行列になります。） 

\[ \bf \bar G=\left[ \begin{array}{ccc} g_{1,1} & 0 & 0 \\ \vdots & \ddots & 0 \\ g_{N,1} & \dots & g_{N,M}\\ \end{array} \right] \tag{6.52} \]

簡略化した行列の次元を N × M とすると、それらは、市場でクォートされている Cap/Floor や Swaption の、行使期日（オプション行使日のPillar）を取るといいでしょう（場合によっては、市場で観測される Black Volatility の Extrapolation が必要です）。すると、\(\bf \bar G\) は、せいぜい 10 × 10 とか 15 × 15 程度の次元数になります。\(\bf \bar G\) から G への補間は、単純な 2 次元の線形補間で十分で、Andersen-Piterbarg は、下記式を示しています(Andersen-Piterbarg 本とは、i,j インデックスの意味が、若干異なりますが、やろうとしている事は一緒です)。 

\[ Part of {\bf \bar G} matrix ....~~~~ \begin{array}{ccc} \bar g_{i-1,j-1} & \dots & \bar g_{i-1,j} \\ \vdots & g_{k,l} & \vdots \\ \bar g_{i,j-1} & \dots & \bar g_{i,j}\\ \end{array} \]

右にある \(\bf \bar G\) の４つの要素、\( \bar g_{i-1,j-1},~\bar g_{i-1,j},~\bar g_{i,j-1},~\bar g_{i,j}\) から、それらの中間にある G の要素 \(g_{k,l}\) を求める式は、下記の通りです。 

\[ \begin{align} g_{k,l} = & \frac {(T_k-T_{i-1})(t_l-t_{j-1})}{(T_i-T_{i-1})(t_j-t_{j-1})} \bar g_{i,j} + \frac {(T_k-T_{i-1})(t_j-t_l)}{(T_i-T_{i-1})(t_j-t_{j-1})} \bar g_{i,j-1} \\ & + \frac {(T_i-T_k)(t_l-t_{j-1})}{(T_i-T_{i-1})(t_j-t_{j-1})} \bar g_{i-1,j} + \frac {(T_i-T_k)(t_j-t_l)}{(T_i-T_{i-1})(t_j-t_{j-1})} \bar g_{i-1,j-1} \tag{6.77} \end{align} \]

このように、簡略化された瞬間 Volatility 行列 \(\bf \bar G\)（の下三角）を使った場合でも、パラメータの数としては依然多く、これでも Over-Fitting の問題が残ります。Andersen-Piterbarg は、この行列の Regularity（滑らかさ）を向上させる項（コスト関数）を目的関数に加える事で、その問題を、若干なりとも回避しようとしています。 

尚、Volatility 関数として、パラメトリックな関数（例えば Rebonato の 4 パラメータ関数）を使った場合、6.74 式と 6.75 式の総和の計算を、Volatility 関数の定積分で行うだけで、通常は解析的に求まります。（あるいは、何等かの求積法を使えば簡単に求まります。） Calibrationアルゴリズムも、以下のアルゴリズムが使え、計算はより簡単になるので、詳細な説明は省略します。 

 

6.5.3.2　  目的関数の設定

Andersen-Piterbarg は、Calibration における目的関数を、複数のウェイト付けされたコスト関数の和とする事で、裁量を柔軟に取り込めるような目的関数の設定方法を紹介しています。 

目的関数に含めるノルムとして、次のような情報を入れます。 

1. Cap/Floor 価格の誤差
2. Swaption 価格の誤差
3. 各 Libor の Volatility 関数の観測時間方向への滑らかさ
4. 各観測時点における Volatility の期間構造（Volatility Curve）の滑らかさ

さらに、1、2、3、4 のそれぞれにウェイトを付け、どれを優先するかを決めます。そのような目的関数を \(\mathscr {I} ({\bf \bar G})\) と置き、次のように定義します。 

\[ \begin{align} \mathscr {I} ({\bf \bar G})=& ~ ω_S \sum_{i=})^{N_s} \frac {1}{N_s}\left(Model_{Swaption,i}({\bf \bar G})-Market_{Swaption,i}\right)^2 \\ & +ω_c \sum_{i=1}^{N_c} \frac {1}{N_c} \left(Model_{Cap,i} ({\bf \bar G})- Market_{Cap,i} \right)^2 \\ & +ω_{∂_t} \sum_{i=1}^N \sum_{j=1}^M \frac {1}{NM} \left(\frac {∂\bar g_{i.j}}{∂t_j}\right)^2 \\ & +ω_{∂_L} \sum_{i=1}^N \sum_{j=1}^M \frac {1}{NM} \left( \frac {∂ \bar g_{i.j}}{∂L_i}\right)^2 \\ & +ω_{∂t^2} \sum_{i=1}^N \sum_{j=1}^M \frac {1}{NM} \left( \frac {∂^2 \bar g_{i.j}}{∂t_j^2}\right)^2 \\ & +ω_{∂L_i^2} \sum_{i=1}^N \sum_{j=1}^M \frac {1}{NM} \left( \frac {∂^2 \bar g_{i.j} }{∂L_i^2 }\right)^2 \tag{6.78} \end{align} \]

但し 

• \(Model_{Swaption,i} ({\bf \bar G})\) ： パラメータ \(\bf \bar G \) による i 番目Swaption のモデル価格
• \(Market_{Swaption,i} \) ： i 番目スワップションの市場価格
• \(Model_{Cap,i} ({\bf \bar G})\) ： パラメータ \(\bf \bar G \) による i 番目 Caplet のモデル価格
• \(Market_{Cap,i} \) ： i 番目 Caplet の市場価格
• \(N_s\) ： Calibration の対象となる Swaption の数
• \(N_c\) ： Calibration の対象となる Caplet の数
• \( \frac {∂ \bar g_{i.j}}{∂t_j} \) ： \(L_i\) の Volatility 関数の ｔ 軸方向への偏微分（差分\( \frac {\bar g_{i,j}~-~\bar g_{i,j-1}}{t_j~-~t_{j-1}}\) で計算）
• \(\frac {∂ \bar g_{i.j} }{∂L_i} \) ： \(t_j\) 時の Volatility curve の Libor 軸方向への偏微分（差分\( \frac {\bar g_{i,j}~-~\bar g_{i-1,j} }{L_i~-~L_{i-1}}\) で計算）
• \( \frac {∂^2 \bar g_{i.j} }{∂t_j^2} \) ： \(L_i\) の Volatility 関数の ｔ 軸方向への二階偏微分（差分で計算）
• \( \frac {∂^2 \bar g_{i.j} }{∂L_i^2} \) ： \(t_j\) 時の Volatility curve の Libor 軸方向への二階偏微分（差分で計算）
• \(ω_S,~ω_c,~ω_{∂t},~ω_{∂L_i},~ω_{∂t^2},~ω_{∂L_i^2}\) ： 各コスト関数へのウェイト。順番に、スワップション価格の誤差、Caplet 価格の誤差、Volatility 関数の ｔ 方向への一階微分（差分）、Volatility 関数の \(L_i\) 方向への一階微分（差分）、Volatility 関数の ｔ 方向への二階微分（差分）、Volatility 関数の \(L_i\) 方向への二階微分（差分）

6.78式をよく見れば分る通り、各項（各コスト関数）は  

• 第１項は、スワップション価格の乖離度合いのコスト関数
• 第２項は、Caplet価格の乖離度合いのコスト関数
• 第３項と第５項は、\(L_i\) の Volatility 関数の時間軸方向への滑らかさのコスト関数。先ほどのグラフで言えば、この項をできるだけ小さくする事によって、点線のカーブの滑らかさを向上させます。
• 第４項と第６項は、各観測時間 \(t_j \) における Volatility curve の滑らかさのコスト関数。先ほどのグラフで言えば、実線のカーブの滑らかさをコントロールします。

それぞれ、どの項を優先するかは、各項のウェイトで調整します。既に述べたように、LMM をスワップション価格へ Calibration しようとすると、どうしても Volatility 関数に不自然な凸凹が発生します。第３項から第６項までは、その欠点を幾分なりとも補正しようとするものです。 

6.78 式の目的関数は、Calibration 対象における両極の考え方の中間をうまく取れるように考えられたものですが、どれを優先するかは、ユーザーの主観的な判断になります。市場価格へのフィットを優先するか、ヘッジ戦略の有効性を優先するか、評価対象商品との整合性を優先するか、事務負担を優先するか等々、様々な判断基準があり、試行錯誤を繰り返しながら決めていく事になります。このように、ウェイトをユーザーが自由に変更できると、恣意的な時価評価につながる危険があります。LMM のように難易度の高いモデルでは、仮にユーザー（トレーダー）が、それを恣意的に変えたとしても、リスク管理部門やプロダクトコントロール部門が、それに異議を唱えるのは、なかなか難しいでしょう。ウェイトを決めたユーザーに、その理由をきちんと説明する説明責任を負わすべきでしょう。 

6.78 式の第１項と第２項は、モデル価格と市場価格の誤差をコスト関数としていますが、実務では、誤差を価格ではなく、Implied Black Volatility の誤差で測る方法を取る所が多いと思います。価格での誤差は、Deep out of the Money の価格誤差が過少評価され、期間の長いオプションの価格誤差が過大評価される嫌いがあるからです。 Volatility 関数として、Rebonato の 4 パラメータ関数などを使う場合、第 3 項～第 6 項のスムーズ化のコスト関数は不要です。 

 

6.5.3.3　  Calibrationアルゴリズム

Calibration の目的関数が決まった所で、いよいよ具体的な Calibration のアルゴリズムを走らせます。その前に、各観測時点 \(t_j\) における相関行列の低ランク近似　\(ρ(t_j)\) を求め、さらにそれを分解した行列 \(\bf C(t_j)\) を求めておきます。観測時点が変わると、いくつかのフォワード Libor は寿命を終え消えていくので、相関行列の次数も次第に減っていきます。すると、仮に相関行列の生き残っている要素の値は全く変わらなくても、低ランク近似された相関行列は、少しずつ変化します。その為の修正操作です。さらに、生き残っているフォワード Libor の数が、モデルのブラウン運動の次元 ｍ を下回ってくる場合、\(\bf C(t_j)\) 行列で不要な行ベクトルの要素は 0 と置いておきます。そして、次のようなアルゴリズムを走らせます。 

1. パラメータ行列 \(\bf \bar G\) の初期値を設定
2. \(\bf \bar G\) から、6.77 式を使って線形補間を行い、\(\bf G\) のすべての要素を求める
3. \(\bf G\) を使って 6.78 式の目的関数を計算。その際、モデルの Caplet 価格、Swaption 価格は、それぞれ 6.74 と 6.75 式で導出された Implied Black Volatilityを使う。
4. \(\bf \bar G\) の値を修正し、２～３ のアルゴリズムを、6.78 式が最小値に収束するまで再計算。
5. 収束した時点の \(\bf G\) と \(\bf C(t_j)\) から、\(ϕ_i~ψ(t_j,T_i),~~i=1,…,n,~~j=1,…,m\)を導出。

上記のアルゴリズムの １～４ の再帰計算は、多変数の Solver を使って解きます。 

 

6.5.3.4　  Calibration アルゴリズムの高速化

Volatility 関数として、Piecewise Constant な行列を選択し、上記のような Calibration アルゴリズムを走らせる場合、最適値を求める変数の数は、行列 \(\bf \bar G\) の下三角の要素すべてになり、その数は数十個になります。これだけの数の多変数の最小値問題を、Solver を使って解く場合、それ相応の時間がかかります。それでも、近年では、コンピューターのハードウェアの能力と、Solver の能力向上によって、1分以内で計算できるようです。しかし、Calibration アルゴリズムのプログラムを工夫する事によって、さらなる Calibration アルゴリズムの高速化は可能です。 

アルゴリズムの中で、求めるべきパラメータの導出過程で、あるパラメータの値が他のパラメータに依存しないか、あるいは依存してもごく軽微な場合、そのパラメータだけ先に求めるアルゴリズムを走らせると、一般的には高速化が可能です。\(\bf \bar G\) の各行の要素は、その行に対応する Libor よりも期間の短いベンチマーク商品にしか依存しないので、行の上から順番に計算していけば、ある程度の高速化は可能です。Brigo-Mercurio 本では、それを“Cascade Calibration”アルゴリズムとして紹介しています。 

さあ、これで Calibration も終わり、LMM のモデルが完成しました。これで、LMM を使った金融商品の価格評価が、可能になります。価格評価には、モンテカルロシミュレーションを使う事になりますが、次に、それについて解説したいと思います。