上級編 3. 基本的な金利オプション
3.4 Swaption
3.4.1 BlackモデルのSwaptionへの援用
Blackモデルは、もうひとつの代表的な金利オプションであるヨーロピアンSwaptionの価格評価にも使われています。フォワードスタート金利スワップを対象資産とし、その固定レートの確率過程をBlackモデルで仮定する事により、そこからフォワードスワップ金利の確率分布が特定できます。さらにそれを使った期待値計算によりオプション価格が導出 できそうです。
その場合のPayoffの計算ですが、Capletと異なり、対象資産となる金利スワップには複数のCash Flowがあるので、注意が必要です。オプション行使時において、そのCash Flowは未実現であり、Payoffの計算では、各金利発生日からオプション行使日まで、Cash Flow価値をDiscountする必要があります。CapletではCash Flowが1本しか無く、それに対応するDiscount Factorが、確率変数であるフォワードLIBOR金利の期待値から求まりました。ところがSwaptionでは、複数あるCash Flowに対応するDiscount Factorがそれぞれ必要です。しかし、1個のフォワードスワップ金利だけでは、行使時における期間構造を勘案したイールドカーブ(Discount カーブ)を構築する事が出来ません。
この問題は、各Cash Flow時点のDiscount Factorに相当するゼロクーポン債の集合全体をニュメレールと考える事によって解決しています。
3.4.2 金利スワップの、Discount Factorによる関数表現
まず対象資産となる金利スワップのキャッシュフローが以下の図のようになると仮定します。すなわち、みなし元本=1とし、スタート時のエンド時の元本交換は無く、変動金利と固定金利Cash Flowの交換が、各クーポン日に発生すると仮定します。
(簡略化して、固定金利と変動金利の支払い日が同じ、金利期間は一律 τ としています)
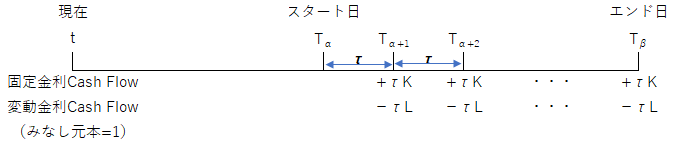
ここで、時点=t における、\(T_{\alpha}\) スタート\(T_{\beta}\)エンドとなるフォワードスワップレートを \(S_{α,β}(t)\) と表記します。
すると \(S_{α,β}(t)\) は、t 時におけるLIBOR-Swapカーブから、各 Cash Flow時の Discount Factor(:=ゼロクーポン債価格 \(P(t,T_i)\) )を使って、次の様に表現できます。(有名な公式です。導出方法は、”基礎編 3.5.2 AnnuityとDiscount Factorとスワップ金利の関係”参照)
\[ S_{α,β}(t)=\frac{P(t,T_α )-P(t,T_β)}{\sum_{i=α+1}^β τ P(t,T_i)} \tag{25} \]分母にある級数は、Annuityの現在価値と呼ばれています。
3.4.3 Swaption価格式の導出
(i) SwaptionのPayoffの期待値
ここで、行使日が、スワップのスタート日すなわち \(T_α\) で、行使価格(固定金利のストライクレート)が K のヨーロピアンPayer Swaptionを考えます。Payer Swaptionとはオプション保有者が、ストライクレート K で固定金利支払いのスワップを取組む権利を持つオプションの事です。すると、この Swaptionの \(T_α\) 時点の payoffは
\[ Payoff(T_α)=max\left[(S_{α,β}(T_α)-K),\ 0\ \right]×\sum_{i=α+1}^β τ P(T_α,T_i) \]となります。さらに、現時点 t におけるこの期待値に \(T_α\) からtまでの Discount Factorを使って現在価値に直した値が、Swaptionの現在価値になります。すなわち
\[ SwaptionPrice(t)=P(t,T_α) E^{Q_{RN}}\left[max\left[(S_{α,β}(T_α)-K),\ 0\ \right]×\sum_{i=α+1}^β τ P(T_α,T_i)\right] \tag{26} \]期待値計算に使うリスク測度は、リスク中立測度(Risk Neutral Measure)とし、それを \(Q_{RN}\) と表記しています。
(ii) Annuityファクターをニュメレールと考える
さて、ここで当初指摘した問題点が出てきました。(26)式の期待値計算中にある \(\sum_{i=α+1}^β τ P(T_α,T_i)\) の値が、満期時の \(S_{α,β}(T_α)\) からだけでは特定できません。\(S_{α,β}(T_α)\) の値は1個しか無く、そこから複数のゼロクーポン債のポートフォリオである Annuityファクターは導出できません。
これについては、一般的に、測度変換のテクニックを使って、問題を解決しています。すなわち、このAnnuityをニュメレールとして、オプション価値の相対価格の期待値計算を行うと、期待値計算の中にあるAnnuityファクターが消えてしまうのです。
t時におけるAnnuityファクターの価格を
\[ \sum_{i=α+1}^β τ P(t,T_i):=A(t) \tag{27} \]と置きます。このAnnuityファクターをニュメレールとすると、Swaption価格とニュメレールとの相対価格の変動はマルチンゲールとなるので、
\[ \begin{align} \frac{SwaptionPrice(t)}{A(t)} &=E^{Q_A} \left[\frac{SwaptionPrice(T_α)}{A(T_α)}\right] \\ &=E^{Q_A} \left[ \frac{Payoff(T_α)}{A(T_α)}\right] \\ &=E^{Q_A} \left[ \frac{max[(S_{α,β}(T_α)-K),\ 0\ ]×A(T_α )}{A(T_α)}\right] \\ &=E^{Q_A} \left[max[(S_{α,β}(T_α)-K),\ 0\ ]\right] \end{align} \]となります。ここで左辺のA(t)を右辺に移すと
\[ SwaptionPrice(t)=A(t)E^{Q_A} \left[max[(S_{α,β}(T_α)-K),\ 0\ ]\right] \tag{28} \]となります。A(t) は(27)式の通り、現時点のイールドカーブから計算できます。
(iii) Swaptionの価格式
(26)式から \(A(T_α)=\sum_{i=α+1}^β τ P(T_α,T_i)\) が消えたので、あとは Payoffの期待値を計算すれば t 時の Swaption価格が求まります。
Payoffの期待値は、Capletと同様にBlackの公式を使って求まるので
\[ \begin{align} SwaptionPrice(t) &=A(t)×Black(S_{α,β}(t),K,σ) \\ &=A(t)×\left[S_{α,β}(t) \Phi(d_1)-K\Phi(d_2)\right] \tag{29}\\ & 但し\\ & d_1= \frac{ \ln \frac{S_{α,β}(t)} K + \frac 1 2 σ^2}{σ},\ \ \ d_2= \frac{ \ln \frac{S_{α,β}(t)} K - \frac 1 2 σ^2}{σ} \end{align} \]となります。計算の途中経過は、Capletの価格式を導出した過程と同じなので、省略します。
3.4.4 Multi-Curve対応の場合のAnnuityファクター A(t)について
Capletのセクションの補論でも述べましたが、ここでもMulti-Curve対応について考える必要があります。(26)式で使われているDiscount Factorは、2種類あります。1つは期待値計算の外にある \(P(t,T_α)\)(\(T_α\) から現時点 t までの Discount Factor)で、もう1つは期待値計算の中にある \(\sum_{i=α+1}^β τ P(T_α,T_i)\)(各Cash Flow時点 \(T_i\) から、スワップ行使時点 \(T_α\) までの Discount Factor)です。両者は、Annuityファクターをニュメレールとすることで、(28)式中で、A(t)に一本化されています。しかし(26)式の成り立ちから考えると、\(T_α\) から t までの Discount Factorと、各Cash Flow日である \(T_i\) から、オプション行使日の \(T_α\) までのフォワードDiscount Factorの積に分解できます。すなわち
\[ A(t)=P(t,T_α) \sum_{i=α+1}^β τ P(t,T_α,T_i) \]となります。(但し、\(P(t,T_α,T_i )\) は、\(T_i\) 満期のゼロクーポン債の、t 時における \(T_α\) フォワード価格)
シングルカーブでは、両方のDiscount Factorを1本のLIBOR-SWAPカーブから導出すればいいでしょう。しかしMulti-Curve対応では、両者のDiscount Factorを別々のイールドカーブから導出する必要があります。すなわち後者のDiscount Factorは、LIBOR-Swapカーブから導出しますが、前者のDiscount Factorは、OISカーブから導出する必要があります。
この場合A(t)は、次の様に分解できます。
\[ A^{MultiCurve}(t)=\sum_{i=α+1}^β τ P(t,T_i)= P^{OIS}(t,T_α) \sum_{i=α+1}^β τ P^{LIBOR}(t,T_α,T_i) \]但し、\(P^{OIS}(t,T_α)\) は OISカーブから導出された Discount Factorで \(P^{LIBOR}(t,T_α,T_i)\) は LIBOR-Swapカーブから導出された、フォワードDiscount Factor。
この \(A^{MultiCurve}(t)\) を、ニュメレールとすると、これまでと同様の解析プロセスを経て、下記のような Swaptionの価格式が導出できます。
\[ \begin{align} SwaptionPrice(t) &=P^{OIS}(t,T_α) \sum_{i=α+1}^β τ P^{LIBOR}(t,T_α,T_i) ×\left[S_{α,β}(t) \Phi(d_1)-K\Phi(d_2)\right] \tag{30}\\ & 但し\\ & d_1= \frac{ \ln \frac{S_{α,β}(t)} K + \frac 1 2 σ^2}{σ},\ \ \ d_2= \frac{ \ln \frac{S_{α,β}(t)} K - \frac 1 2 σ^2}{σ} \end{align} \]3.4.5 Cash-Settled Swaption
Swaptionが行使された場合の決済方法として、対象スワップを取組むのではなく、オプション行使時の時価で現金決済を行う場合があります。この時価評価には、スワップ金利のキャッシュフローを行使日までDiscountするAnnuityファクター \(A(T_α)=\sum_{i=α+1}^β τ P(T_α,T_α,T_i)\) の値が必要になりますが、この計算方法が米国市場と、欧州市場で、若干異なっています。
米国市場では、Swaption行使時のイールドカーブ(LIBOR-Swapカーブ)から導出し、その時点の金利の期間構造を勘案します。一方、欧州市場の取引慣行では、行使時の金利スワップレート \(S_{α,β}(T_α;T_α,T_β)\) を使って、フラットなイールドカーブを想定し、そこから Annuity価格を導出します。式で表すと、下記のようになります。
\[ A^{FlatCurve}(T_α;T_α,T_β)=\sum_{i=α+1}^β τ P^{FlatCurve}(T_α;T_α,T_i) =\sum_{i=α+1}^β τ \frac{1}{(1+S_{α,β}(T_α ))^{(T_i-T_α)}} \tag{31} \]このAnnuityファクターは、あくまでSwaption決済用の式であり、市場で観測されるLIBOR-SWAPカーブから導出できません。従って、このAnnuityファクターをニュメレールとして使う事はできません。
(ニュメレールは、価格が 0 にならない市場で取引される商品でなければなりません。“市場で取引出来る”とは、市場のイールドカーブから、間接的に導出されるゼロクーポン債や、フォワード金利なども含まれます。それらは、プレーンな金利スワップ取引のロングとショートの組合せで構築できるからです。しかし、上記の式にある \(P^{FlatCurve}(T_α;T_α,T_i)\) は、それが出来ません。)
この場合、ニュメレールとして、(27)式のAnnuityファクターを使った場合、\(S_{α,β}(T_α)\) の相対価格の変動はマルチンゲールになりません。マルチンゲールでなければ、幾ばくかのドリフト項が発生します。そのドリフト項を特定しない限り、(28)式から(29)式までのプロセスによる、正確なSwaptionの価格式の導出が出来なくなります。しかし、現在のように低金利でイールドカーブの傾斜が緩やかな場合、通常のAnnuityファクターとフラットカーブを使ったそれとの差は軽微です。実務では、欧州型の現金決済Swaptionも(29)式を使って時価評価しても、あまり問題ないでしょう。しかし、将来、金利水準が上がり、かつカーブの傾斜がきつくなった場合、この差に注意する必要があります。その場合、Libor Market ModelなどのTerm Structureモデルを使う必要があります。