上級編 6. Libor Market Model
6.2 古典的なLibor Market Model
6.2.2 フォワードLibor の期間構造(Tenor Structure)を設定
まずイールドカーブを現時点から最長期の時点まで、一定のテナー(Libor期間)を持つフォワード Libor で区分します。現時点を t=0、最初の Libor の Fixing 日を \(T_0\)、以後、最長期の時点を \(T_N\) とし、その間を Libor のシリーズに分割します。
スタート日が \(T_{k-1}\) で、エンド日(=金利支払日)が \(T_k\) のフォワード Libor を \(L_k\) と表記します。通常、Libor の Fixing 日はスタート日の 2 営業日前になりますが、ここでは説明の便宜上、スタート日と Fixing 日は同じと仮定します。また、各 Libor の期間を \(τ_k=T_k-T_{k-1}\) と表記します。Libor の期間は 3 か月か 6 か月が一般的で、仮に \(T_N=40\) 年とすると、イールドカーブを約 80~160 のフォワード Libor で分割する事になります。
以上の記法を、図示すると、下記のようなイメージです。
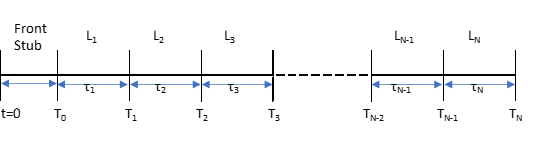
注 : t=0 から \(T_0\) までの期間の Libor は、Front Stub(イールドカーブの一番手前から、次の Libor Fixing日までの半端な期間)と呼ばれており、この期間の金利は t 時に Fixing 済みです。しかし、Front Stub を、\(T_0\) 満期のゼロクーポン債価格と見做した場合、t から \(T_0\) までの間にその価格は変動します。また、LMM では、時間の経過と伴に、手前のフォワード Libor から順番に Fixing 日に金利が確定するものの、そのクーポン支払い日までは、それ自体が新たな Front Stub となり、価格変動リスクにさらされます。これを、どう取り扱うか、あらかじめ考えておく必要があります。これについては、後の方で説明する予定です。
この n 個のフォワード Libor ベクトルは、m 次元(m≦n)のブラウン運動 dw によって駆動されるとします。前のセクションで、測度変換の公式を説明した際、n 個の証券の価格変動を、n 個の独立したブラウン運動が駆動すると仮定しました。しかし、LMM では最大で 80~160 個のフォワード Libor の確率過程を取り扱うので、それらを駆動するブラウン運動の数を同数にすると、非常に複雑なモデルになってしまいます。実務では、駆動するブラウン運動の数を、せいぜい 3~5 個程度に絞って、大幅に簡略化しています。
そのブラウン運動により生成される確率空間を \( \{Ω,~F,~P\}\) と表記すると、各フォワード Libor は、この確率空間上で可測な確率変数になります。ここで、P は、市場で予測される自然な確率測度です(“市場で予測される自然な”という意味はあいまいで、実際にその確率測度を客観的に予測・特定する事は不可能です。しかし、モデルの解析においては、それを特定する必要が無く、そこに拘る必要はありません)。
フォワード Libor のシリーズから、Bootstrapping の要領で、各 \(L_k~の支払日=T_k\) を満期とするゼロクーポン債価格も導出できます。従って、そのゼロクーポン債価格も、この確率空間上の可測な確率変数になります。逆に、そのゼロクーポン債価格が先に判れば、そこからフォワード Libor も導出できます。LMM において、各ゼロクーポン債価格は、ニュメレールとしての役割も果たします。
6.2.3 モデル
初期の LMM の SDE を再記します。
\[ \frac{dL_i(t)}{L_i (t)}= μ_i (t,L(t))dt+σ_i (t)∙ {\bf C∙dw(t)},~~~~~~i=1,2,…,n \tag{6.1} \]先ほどのテナー構造から、n は 80~160 を想定する必要があります。今後の解析のプロセスに合わせる為、この式を若干書き換えます。確率測度については、自然な確率測度ではなく、何等かの同値マルチンゲール測度 Q を使って記述します。また、ブラウン運動のベクトル \( \bf dw^Q (t)\) は m 次元(m≦n)とします。
\[ dL_k=L_k(t)~μ_k^Q(t) dt + L_k~σ_k(t)~∙ {\bf c_k ∙ dw^Q}(t)~~~~~~ k=1,2,…,n \tag{6.27} \]注1 :ここで、SDE における拡散項の表現方法について、若干の解説をしておきます。というのは、様々な文献でその表現方法が異なり、意味が混乱して理解の妨げになると思われるからです。
まず 27 式の \(σ_k(t)\) はスカラ値で、\(L_k\) に対応する変化率 Volatilityです。またベクトル \(\bf c_k\) は、(1)式における行列 C の k 番目の行ベクトルを示します。後ほどの解析プロセスの都合上、拡散係数を \(L_k(t)~\bf σ_i(t)∙C∙dw^P(t)\) (スカラ × ベクトル × 行列 × ベクトル → スカラ値)とせず、\(L_k~σ_k(t)∙ \bf c_k∙dw^P(t)\)(スカラ × スカラ × ベクトル × ベクトル → スカラ値)と表記しています。表記方法は違いますが、いずれも同じ値のスカラ値になります。
また上の式で、\(\bf dw^Q(t)\)は、 m 次元のそれぞれ独立なブラウン運動のベクトルを示しています。フォワードLibor 間の相関は、相関行列を分解した行列 C(すなわち \(\bf ρ=C∙C^{\top}\))で表現され、それが\( \bf dw^Q (t)\) に作用して、\( \bf C∙dw^Q (t)\) が相関のあるブラウン運動のベクトルを形成します。しかし文献によっては、相関の情報を、ブラウン運動の中に含ませているものもあります。例えば、この解説のベースになっている Brigo-Mercurio の本(”Interest Rate Models(2006)” 208ページ)では、互いに相関を持つブラウン運動ベクトル
\( {\bf dz(t)}=\{ dz_1 (t),dz_2 (t),…,dz_m (t) \},~~~dz_i (t)~dz_j (t)=ρ_{i,j}(t)dt\)
がフォワード Libor を駆動する形で、SDE を定義しています。従って、Brigo-Mercurio 本では、\(\bf C∙dw^Q(t)=dz^Q(t)\) あるいは \( {\bf c_k∙dw^Q(t)}=dz_k^Q (t)\) を意味します。
また別の文献では、相関の情報を、Volatility 関数 \(\bf σ_k (t)\) に含めているものもあります。Andersen-Piterbarg の“Interest Rate Modeling”では、Volatility 関数を
\( \bf σ_k(t,L_k,Λ)=Λ(t)∙φ(t,L_k (t))\) というように、相関の情報 \(\bf Λ(t)\) と、t 時のLibor \(L_k(t)\) に依存する Volatility 関数 \(φ(t,L_k)\) の積とみなしています。従って Andersen-Piterbarg の \(\bf σ_k ( )\) は 上記式の \(L_k~ \bf σ_k (t)∙C\) を意味します。Jamishidian の論文(“Libor and Swap Market Models and Measures”1997)でもやはり、\(\bf σ_k(・)\) に、相関の情報を含ませています。
このように、拡散項における相関係数の表現方法が、文献によりまちまちなので、数式を注意して読む必要があります。ここでは、“測度変換の公式”の導出プロセスで使った表現方法を、そのまま使います。測度変換により発生するドリフト項が、拡散項係数からどのように求まるかを理解するには、この表記方法が一番わかりやすいと思うので。
注2 : 当初、証券市場全体の SDE を示す (6.3) (6.3)’ 式の多次元モデルでは、n 個の確率変数を n 個の相関するブラウン運動が駆動し、相関を表す行列 C の次元を n × n としました。実際の LMM では、確率変数の数が 80~160 個となるので、それらの確率変数が、同じ数のブラウン運動により駆動されると仮定するのは、Over-Specification(変数の数を多くしすぎて、逆にモデルの予測性能を落とす)になります。また計算負荷も膨大になるので、現実的ではありません。通常、Libor を駆動するブラウン運動の数は 3~5 で十分です。すると、C のランクは 3~5 で十分という事になります。測度変換の公式を導出する過程で、C はランク n として説明してきましたが、ランクを落としても、その公式はそのまま使えます。以下、Libor を駆動するブラウン運動の数(次元)を m (m<<n) とします。
(27)式は、確率測度を何等かの同値マルチンゲール測度 Q として記述しています。LMM では多数の相関のある確率変数の同時分布を取り扱うので、すべての確率変数(フォワード Libor )について、同じ確率測度で分布を特定する必要があります。すると、その特定した確率測度下でマルチンゲールになるのは、せいぜい 1 個の Libor のみです。もし市場がアービトラージフリーの条件を満たしているならば、他の Libor の SDE には、ドリフトが発生します。そのドリフトの経済的な意味(一種の Convexity 調整)については、後で解説しますが、ここでは、そのドリフトがどの程度になるかを、前のセクションで説明した“測度変換の公式”を使って、解析的に求めたいと思います。