上級編 6. Libor Market Model
6.6 モンテカルロシミュレーション
6.6.4 分散減少法(Variance Reduction Techniques)
6.6.4.3 制御変量法 (Control Variates Methods)
6.6.4.3.1 制御変量法の原理
MCS におけるサンプルの分散値を減少させる方法のひとつに、Control Variates Methods(制御変量法)と呼ばれるテクニックがあります。これは、求めたい確率変数 y(例えばエキゾチックオプションのPayoff)と、極めて相関が高い別の確率変数 x(例えば、そのオプションの対象資産など)を探し出し、その相関関係を利用して y の分散を低減させるテクニックです。但し、制御変量として利用する確率変数 x は、y と同じサンプル上で推定値を求める事が可能で、かつ、その真正の期待値も、解析的に簡単に求まるものに限ります。例えば、オプションの対象資産や、プレーンなヨーロピアンオプションなどです。
もう少し具体的に説明します。まず、MCS で生成される確率変数のサンプルを \(y_i=\{y_1,…,y_N\}\) とすると、そのサンプル平均は \(y_{サンプル平均}=\frac 1 N \sum_{i=1}^N y_i\) で求まります。一方、制御変量として使う確率変数 \(x_i=\{x_1,…,x_N\}\) も、同じシミュレーションで求まるとすると、そのサンプル平均も \(x_{サンプル平均}=\frac 1 N \sum_{i=1}^N x_i\) で求まります。ただし、\(x\) の場合は、MCS を使わなくても、真の平均 E(x) が別途すでに求まっているとします。すると、\(x_{サンプル平均}\) は、シミュレーション値なので、必ず真の平均 \(E(x)\) と誤差が発生します。この誤差は、真の平均が分かっているので、推定誤差ではなく、本当の誤差です。そうすると、\(x~と~y\) に強い相関があれば、\(y_{サンプル平均}\) も \(y\) の真の平均から、同じ割合で誤差が発生していると推察されます。制御変量法は、その誤差分 \(y\) の値を修正して、より真の平均に近づけた \(y_{サンプル平均}\) を求めるものです。その結果 \(y\) の分散は、修正する前と比べ、\(x~ と~ y\) の相関の度合いに従って、相当程度低減されます。
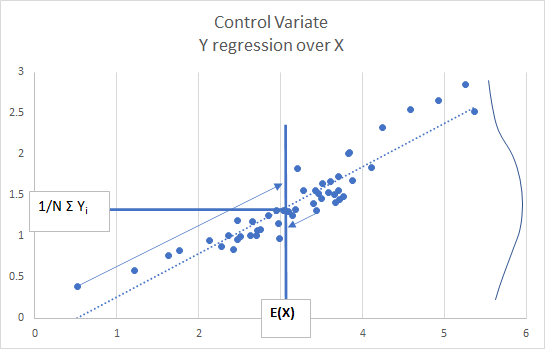
これを、直観でも理解しやすくする為、グラフを使って説明します。下のグラフは、ある MCS で生成された \(x_i,~y_i,~~~i=1,…,n\) の値を、サンプルごとに点 \((x_i,~y_i)\) でプロットし、散布図にしたものです。横軸が制御変量となる確率変数 x で、縦軸が求めたい確率変数 y(例えばPayoffの期待値)の値です。ここでは、関係性のみに着目するので、座標軸の単位は気にしないで下さい。図から、両者に強い正の相関がある事が認められます。MCS で生成されたサンプル値 y は、y 軸にある通り、0.4~3 程度の間に分散しています。グラフから、y の散らばりが、x の散らばりで説明できる部分(横軸への散らばり)と、x と直行するxでは説明できない部分(縦軸への散らばり)で分散している事が判ります。中心にある縦線は x の真の期待値 E(x)で、横線は y のサンプル平均です。さらに、斜めに走る点線は線形回帰による直線で、その傾きを b とします。この傾き b は、サンプルデータを使って下記式により簡単に求まります。
\[ b=\frac {Cov(x,y)}{Var(x)} =\frac {\sum_{i=1}^n \left(x_i-x_{サンプル平均}\right)\left(y_i-y_{サンプル平均}\right)}{\sum_{i=1}^n \left(x_i-x_{サンプル平均}\right)^2} =\frac {ρ_{xy}~σ_x~σ_y}{σ_x^2}=ρ_{xy} \frac {σ_y}{σ_x} \tag{6.86} \]すると、MCS による各サンプル上の x と y の関係式は、
\[ y=bx+ϵ \tag{6.87} \]と表現できます。ε が x の変動で説明できない y の誤差項であり、グラフで言えば縦軸方向への散らばりを表します。
ここで、特定のサンプルで求まった \(y_i\) の値を、同じサンプルで得られた制御変量 \(x_i\) とその真正の期待値 \(E(x)\) を使って下記のように修正します。
\[ \hat {y_i}=y_i-b(x_i-E(x)) \tag{6.88} \]この修正で、何をしようとしているかは、下のグラフをご覧ください。これは、6.88式を使って、すべての \(y_i\) を、制御変量 x と回帰直線の傾き b を使って補正して、\(\hat {y_i}(b)\) に変換した値の散布図になります。
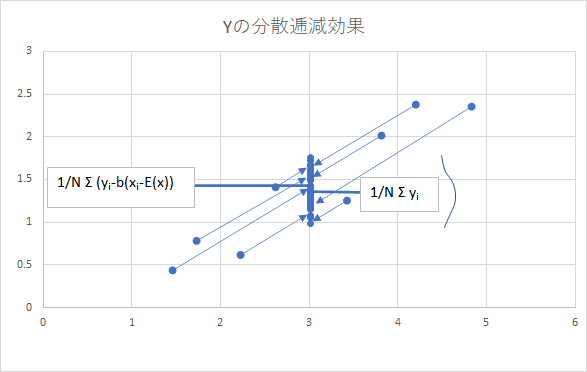
ちなみに、この修正された \(\hat {y}\) のサンプル平均は下記式で求まります。
\[ \hat {y}_{CV平均}=\frac 1 N \sum_{i=1}^N \left[\hat {y_i}-b\left(x_i-E(x)\right)\right] =y_{サンプル平均}-b(x_{サンプル平均}-E(x)) \tag{6.89} \]図から見て明らかな通り、サンプル y の散らばりを、x 方向の散らばりはすべて補正し、x で説明できない(x ベクトルと直行する方向の)ものだけにしています。前のグラフと比べ、y の全体の散らばり度合いが小さくなっている事が判ります。これが 制御変量法 による分散低減効果の仕組みになります。
6.6.4.3.2 制御変量法による分散低減効果
では、この方法により、どの程度 y の分散が低減できるか見てみます。まず、先ほどの回帰直線の傾きを使った x と y の関係式は \(y=bx+ϵ\) でしたが、両辺の分散を取ると下記のようになります。
\[ σ_y^2=σ_x^2+σ_ϵ^2 \tag{6.90} \](注:x と ε は直交しているので、共分散項は消えます)
この式が意味するのは、y の分散は、x で説明できる分散と、x と直交する、x では説明できない ε の分散から成るいう事です。
これが、制御変量法を使った場合にどうなるか、みてみます。その為に、まず \(y=bx+ϵ\) の式を、6.87 式(制御変量を使った y の修正式)に代入します。
\[ \hat {y}=y-b(x-E(x))=bx+ϵ-b(x-E(x))=ϵ-bE(x) \tag{6.91} \]すると、右辺から bx の項が消えるのが分ります。b E(x) は x で説明できる y の期待値を意味します。従って右辺は、それとの誤差を意味します。そして両辺の分散を取ると、下記のようになります。
\[ σ_{\hat {y}}^2=σ_ϵ^2 \tag{6.92} \](注: 6.91 式の第2項の bE(x) は、決まった値を取るので、分散は 0 です)
すなわち、すなわち、制御変量を使って修正された \(\hat {y}(b)\) の分散は、y の変動から x (と同じ方向の)の変動要因を取り除いた、残りの ε 要因による分散を意味します。先ほど、グラフで説明した通りです。
では、この \(σ_{\hat {y}}^2\) と、もともとのサンプル分散 \(σ_y^2\) を比較し、どの程度小さくなっているか見てみます。6.88 式の両辺の分散を取ると、下記のようになります。
\[ σ_{\hat {y}}^2 =Var [y-b(x-E1(x))]=Var[y-bx]=σ_y^2 - 2b ρ_{xy}σ_x σ_y + b^2 σ_x^2 \]さらに、右辺の b は、6.86式から \( b=ρ_{xy} \frac {σ_y}{σ_x}\) なので、これを代入すると、
\[ \begin{align} & σ_{\hat {y}}^2=σ_y^2- ρ_{xy}^2 σ_y^2=σ_y^2 (1-ρ_{xy}^2 ) \\ & ∴ \frac {σ_{\hat {y}}^2S}{σ_y^2} =1-ρ_{xy}^2 \tag{6.93} \end{align} \]となります。これが、制御変量による分散低減効果を示す式です。左辺は、制御変量を使った補正後の \(\hat {y}\) の分散に対する、補正前の y の分散の比です。その比は、x と y の相関が強ければ強いほど、\(1-ρ_{xy}^2\) は小さくなり、y の分散値が低減される事になります。例えば、相関係数が 0.9 であれば、右辺は約 0.2 となり、分散は約 1/5 に低減されます。
6.6.4.3.3 制御変量(Control Variates)の選択
価格評価に LMM を使わざるを得ない商品は、大半が複雑な Payoff 条件を持つエキゾチックデリバティブズになります。そういった商品の価格と強い相関をもつ制御変量を探すのは、簡単ではありません。前のセクションの説明から判る通り、効果的な制御変量 x になり得る確率変数は、下記の要件を満たす必要があります。
- 求めるべき確率変数 y の期待値と、強い相関のあるもの
- 将来時点における価格(期待値)が、簡単に(できれば解析的に)求まる事
- y と同じ MCS で、y のサンプルごとに価格が求まるもの
この 3 要件を満たす制御変量として、具体的にどのようなものが候補になり得るか、見てみます。
(1) 対象資産
典型的なものは、オプションの対象資産(金利、インデックスなど)です。そもそも MCS でシミュレーションされるのは、対象資産の価格(または 金利やインデックスレベル)なので、上の3つの要件の内、3は簡単に満たします。また、対象資産が市場で取引されている商品であれば、その価格(あるいは金利、インデックス)は、リスク中立測度下でマルチンゲールになるので、その真正の期待値も、現時点の価格(金利、インデックス)から簡単に求まります。従って2の要件も簡単に満たせます。しかし、相関については、商品によっては、必ずしも強い相関がある訳ではありません。例えば、オプションの場合、ストライクが Deep Out of the Money の場合、MCS のサンプル経路のほとんどで、Payoffは 0 となります。すると、その範囲では相関が 0 なので、対象資産の価格(金利、インデックス)との相関は、期待するほど大きくなりません。
(2) オプション価格
あまり一般的ではありませんが、オプションを制御変量に使うとうまくいくケースがあります。MCS が使われるのは、通常、LMM のような複雑なモデルを使う場合で、オプション行使時における分布が解析的に求まらないケースです。そうすると、要件の2と3を同時に満たすようなオプションを探すのは簡単ではありません。
経路依存型のオプション(例えば算術平均型のアジアンオプション)の価格評価をする場合、モデルは Blackモデルのようなシンプルなもの使った場合でも、価格評価には MCS が使われる事があります。(算術平均型)アジアンオプションは、ストライク価格を、過去の一定期間における対象資産の算術平均で決めるオプションで、その価格は、Black モデルを使った場合でも、解析的に求まりません。しかし、ストライク価格を、幾何平均で求めるアジアンオプション価格は、解析的に求める事が可能です。すると、(算術平均型)アジアンオプションの価格を MCS で求める場合、幾何平均型のアジアンオプションを制御変量として使うと、非常に効果的に分散低減が図れます。両者の価格は、同じ経路を使っても、微妙に異なりますが、価格の相関は非常に強くなります。
(3) 近似されたモデルを使った対象資産
要件2と3を満たすには、価格評価対象となるデリバティブズ価格 y と、制御変量となる確率変数 x が、同じモデルで MCS のサンプル毎に価格評価され、かつ制御変量 x については、同じモデルで解析的に価格が求まる必要があります。上記の例での、対象資産や、オプションは、そういった確率変数です。
“同じモデル”の要件を若干緩めて、制御変量の価格評価で使うモデルを、y 用のモデルと類似しているものの、よりシンプルなモデルを使う方法もあります。例えば、y の価格評価を、古典的な LMM(例えば、拡散項係数が Piecewise Constantな関数)を使って行うものの、制御変量 x のモデルは、LMM において、ドリフト項を t=0 時の値で固定するモデルを使うといった方法です。LMMにおけるドリフト項係数は、各離散時間のスタート時点におけるフォワードLiborのベクトルに依存します。従って、MCS における各サンプル経路を生成するにあたり、ドリフト項はランダムに値が決まっていきます。それを、t=0 時点のLiborベクトルに固定してしまえば、幾何ブラウン運動のモデルになり、x の期待値は、解析解ではなくても、MCS よりは簡単な数値解で求める事が可能です。また、その簡易モデルを、MCS で使う乱数列と同じ乱数列でサンプル経路を生成し、サンプル経路ごとに x の価格も計算できます。すると、制御変量法のテクニックが使えます。x は y と同じオプション Payoff にしておけば、非常に高い相関関係が得られるので、かなり大きな分散低減効果が得られます。ただし、x のサンプル毎の価格評価は、同じ乱数列を使うにしても、y と同程度の計算時間がかかるので、同じサンプル数で倍近い計算時間がかかります。
(4) 複数の制御変量を使う
MCS で求めたい確率変数 y のサンプル平均の修正の為に、複数の制御変量を使う事も可能です。Payoff 関数 y が、例えばスプレッドオプションやバスケットオプションのように、複数の確率変数に依存するような場合、それらを制御変量に加える事により、y の分散をより低減できる事があります。あるいは、Cap と Floor の両方の条件が付いた変動金利キャッシュフローを持つデリバティブズでは、制御変量として、複数のオプションを使う事で、より高い分散低減の効果が得られる事があります。
そういった場合でも、当然、それらの制御変数のベクトル x は、y との強い相関関係があり、すべて MCS のサンプル毎に価格計算が出来て、かつその真正の期待値 E(x) が解析的に求まる事が条件です。
複数の制御変量を使う場合、y と ベクトル x の関係を、多重回帰分析で、係数ベクトル b を求める事になります。
\[ y=b_1 x_1+b_2 x_2,…+ϵ ~~~~~ or~~~~~ y=\mathbf {b∙x}+ϵ,~~~~ \bf{b}=\{b_1,b_2…\} \]この係数ベクトルを使い、サンプルごとの y の値を下記式で補正します。
\[ \hat {y_i}=y_i- \bf {b \cdot (x-E(x)) } \]さらにこの補正されたサンプルを使い、サンプル平均を求めます。
\[ \hat {y}_{CV平均}=y_{サンプル平均}- \bf {b \cdot (x_{サンプル平均}-E(x)) } \]制御変量となる確率変数の候補と要件は、1個の制御変量の場合と同じです。ひとつひとつの x と y の相関がそれほど大きくなくとも、ベクトル x 全体でみれば y の説明力が上がり、誤差項 ε を低減させ、分散低減効果が大きくなります。しかし一方で、制御変量を増やすと、その価格計算に、より時間がかかるので、説明能力の低い制御変量をむやみに加えるのは避けるべきです。
(5) 最もシンプルな方法
制御変量となる3つの要件を、確実に満たす変数として、モデルを駆動するブラウン運動があります。各サンプル経路を駆動するブラウン運動を、Payoff 時までつなげていけば、Payoff 時の分布は、平均 0、分散 T(Payoffまでの期間)の正規分布になります。モデルを起動するブラウン運動なので、当然ながら Payoff と何等かの相関を持つでしょうし、かつ期待値が 0 となるのは自明です。追加の計算負荷もほとんど 0 なので、極めて簡単に使える制御変量になります。
以上が、おおまかな制御変量法(Control Variates Methods)についての説明です。使える制御変量を探すのは、商品毎に慎重に行う必要がありますが、制御変量としての要件を満たし、かつ Payoff 関数 y と強い相関があれば、まずまずの分散低減効果が期待できます。ただ、エキゾチックデリバティブズの Payoff 関数は、複雑であり、それと強い相関のある確率変数を探す作業は、商品性に対する深い理解が必要です。場合によっては、せっかく選んだ制御変量が、対象資産の価格変動により Payoff が Deep Out of the Money になった場合、分散低減の効果が薄れ、制御変量法を使う意味がなくなる事も起こり得ます。