上級編 6. Libor Market Model
6.6 モンテカルロシミュレーション
6.6.5 離散化によるバイアス
6.6.5.3 2次のオーダーでの近似スキーム
オイラースキームは、離散化バイアスが、h に対し 1次のオーダーで弱収束する近似スキームになります。弱収束を示す式を再記します。
\[ \left| E \left[ f( \hat{X} ^{(h)} (t))\right]-E\left[ f(X(t)) \right] \right| ≤ c~h \tag{6.111} \]離散化バイアスを2次のオーダーの収束速度 \(o(h^2)\) に加速するには、6.109 式の第 2 項と第 3 項にある積分を離散近似する際、被積分関数である \(a({\bf L}(t))~~と~~{\bf b}(L_i (t))\) を t 時の値で固定せず、t→t+h 間の変動を考慮しなければなりません。その為に、t→t+h 間での \(a({\bf L}(u)),~ と~~{\bf b}(L_i (u))~(但し t ≤ u ≤t+h)\) の関数形を導出し、それを使って、積分を解析する必要があります。ところが、いずれの関数も、確率変数を引数に取っており、解析には伊藤の公式を使う事になります。LMM のような複雑なマルチファクターモデルでは、その解析は非常に複雑で、仮にうまく解析できたとしても、計算に非常に時間がかかる事になります。おそらく、LMM で2次のオーダーの離散スキームは、あまり使われていないのではないかと推察しますが、他のモデルで使う可能性を考え、2次の近似スキームの導出プロセスだけ簡単に解説したいと思います。マルチファクターモデルだと複雑になるので、シングルファクターモデルで解説を進めます。
(1) まず、被積分関数である \(a({\bf L}(u))~~と~~ b(L_i(u))\) について、t→t+h 間の関数形を、伊藤の公式を使って求めます。
(1)―① まず \(a({\bf L}(u))\) から:
u 時(u > t)の \(a({\bf L}(u))\) は、初期値となる \(a({\bf L}(t))\) が与えられれば、伊藤の公式を使って、下記のような積分形式で表現できます。(但し、下記では、a(・) の引数を、\(\bf L(s)\) とせず、簡略化して単に時間 s の関数として表記しています。また、\(a'(s)\) は s での1階微分、\(a''(s)\) は2階微分を示します。)
\[ a({\bf L}(u))=a({\bf L}(t))+\int_t^u \left[a(s)a'(s)+ \frac 1 2 b^2(s)a''(s))\right]ds +\int_t^u a'(s)b(s)dw(s) \]ここで、この式の第 2 項と第 3 項の被積分関数は解析できないので、t 時の値で固定して近似します。すると下記のようになります。
\[ a({\bf L}(u)) \approx a({\bf L}(t))+\left[a(t)a'(t)+ \frac 1 2 b^2(t)a''(t))\right] \int_t^u ds +a'(t)b(t)\int_t^u dw(s) \tag{6.112} \](1)―② 次に \(b(L_i(t))\) :
同様に、\(b(L_i(t))\) についても、伊藤の公式を使って、u 時(u>t)の関数形を導出します。初期値 \(b(L_i(t))\) が与えられると \(b(L_i(u))\) は下記式のようになります。
\[ b(L(u))=b(L(t))+\int_t^u \left[b(s)b'(s)+ \frac 1 2 b^2(s)b''(s))\right] ds +\int_t^u b(s)b'(s)dw(s) \]ここでも、第 2 項と第 3 項にある被積分関数を、t 時の値で近似し、以下のような近似式を導出します。
\[ b(L(u)) ≈ b(L(t))+\left[b(t)b'(t)+ \frac 1 2 b^2(t)b''(t))\right] \int_t^uds+b(t)b'(t) \int_t^u dw(s) \tag{6.113} \](2) 上記 (1) で求めた \(a(L(u))~と~b(L(u))\) の近似式を、6.109 式の積分の被積分関数として使います。
(2)―① まず \(\int_t^{t+h} a({\bf L}(u))du\) から:
6.112 式で求めた \(a(L(u))\) を、6.109 式の第 2 項に代入します。すると
\[ \begin{align} \int_t^{t+h} a({\bf L}(u))du ≈ & a(t)h+\left[a(t)a'(t)+ \frac 1 2 b^2(t)a''(t))\right]\int_t^{t+h}\int_t^u dsdu \\ & +b(t) a'(t) \int_t^{t+h} \int_t^u dw(s)du \tag{6.114} \end{align} \]上式の中に、2重積分の項が2つ残っています。2次の近似スキームを完成させるには、これらの値を解析的に求めるか、シミュレーションで求める必要があります。その方法は、後で説明します。
(2)―② 次に \(\int_t^{t+h} b(L_i(u))dw(u)\) の導出:
6.113 式の \(b(L_i(u))\) を 6.109 式の第3項に代入すると
\[ \begin{align} \int_t^{t+h} b(L_i(u))dw(u) ≈ ~ & b(t)(w(t+h)-w(t)) \\ & + \left[b(t)b'(t)+ \frac 1 2 b^2(t)b''(t))\right]\int_t^{t+h} ∫_t^u dsdw(u) \\ & + b(t)b'(t) \int_t^{t+h} \int_t^u dw(s) dw(u) \tag{6.115} \end{align} \]ここでも、第2項と第3項に2重積分が残っています。これらの解析は後で示します。
(3) 上記で求めた積分(6.114 と 6.115式)を、 6.109 式に代入します。すると、2次のオーダーの離散近似式は以下のようになります。
\[ \begin{align} L_i(t+h) & ≈ ~ L_i (t) \\ & {\small + a(t)h+ b(t)(w(t+h)-w(t))} \\ & {\small + \left[a(t)a'(t)+ \frac 1 2 b^2(t)a''(t))\right] \int_t^{t+h}\int_t^u dsdu + b(t)a'(t)\int_t^{t+h}\int_t^u dw(s)du }\\ & {\small + \left[b(t)b'(t)+ \frac 1 2 b^2(t)b''(t))\right] \int_t^{t+h}\int_t^u dsdw(u) +b(t)b'(t) \int_t^{t+h}\int_t^u dw(s)dw(u) } \tag{6.116} \end{align} \]式が長くて解り辛いのですが、この式は次のような意味です。
\(L_i(t+h) ≈ L_i \) の初期値
+ \(L_i\) の1次の近似式
+ ドリフト項の2次の近似式
+ 拡散項の2次の近似式
(4) 2重積分の解析 : 6.116 式に現れた4種類の2重積分を解析します。
(4)―① \(\int_t^{t+h}\int_t^u ds du~~ と~~ \int_t^{t+h}\int_t^u dw(s)dw(u) \) :
この2つの2重積分は以下のように解析できるので、それを使います
\[ \int_t^{t+h}\int_t^u dsdu= \frac 1 2 h^2 \tag{6.117} \] \[ \int_t^{t+h}\int_t^u dw(s)dw(u)= \frac 1 2 \left((Δw)^2-h\right) \tag{6.118} \](4)―② \(\int_t^{t+h}\int_t^u dsdw(u)\) :
この2重積分は、次のように変形できます。
\[ \begin{align} ∫_t^{t+h}∫_t^u dsdw(u) & =∫_t^{t+h} (u-t) dw(u) \\ & = h w(t+h)-∫_t^{t+h} w(u)du \\ & = h\left[w(t+h)-w(t)\right]-∫_t^{t+h} \left[w(u)-w(t)\right]du \\ & =h Δw-∫_t^{t+h} ∫_t^u dw(s)du \tag{6.119} \end{align} \]この式の最後に残った2重積分は、まだ未解析の2重積分\(∫_t^{t+h}∫_t^u dw(s)du\) と同じです。最終的にこれをどう解析するかです。
(4)―③ \(∫_t^{t+h}∫_t^u dw(s)du\) のシミュレーション
この2重積分だけは、解析的に求まらず、シミュレーションで近似する事になります。2重積分をよくみると、内側の積分はブラウン運動の積分で、t から u までの変化になります。外側の積分は、それを、t から t+h まで積分しています。すなわち、下記のように書き換えられます。
\[ ∫_t^{t+h} \left(w(u)-w(t)\right)du ≡ I_{Δw} \]これをグラフで表記すると、この積分は下記のように \(w(u)\) の軌跡の面積(但し、負のエリアは、マイナスして計算)に該当します。
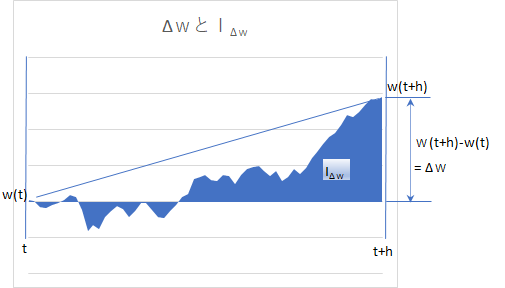
\(w(u)\) がランダムに動くので、この積分の値をどうシミュレーションするかですが、Paul Glasserman本では、下記のように、\(w(t+h)-w(t)=Δw~~ と~~ I_Δw\) は、相関を持ちながら同時正規分布する事が示されています。
\[ \begin{pmatrix} Δw \\ I_{Δw} \end{pmatrix} ~~ \sim ~~ \mathcal {N} \left[0, \begin{pmatrix}h & \frac 1 2 h^2 \\ \frac 1 2 h^2 & \frac 1 3 h^3 \end{pmatrix} \right] \]その導出過程の説明は省略させて頂きますが(Paul Glasserman本を参照して下さい)、 \(I_{Δw}~~ と~~Δw\) と相関がありそうなことは、図をみれば直観で感じ取れると思います。
分散共分散行列から、相関行列を導出するのは簡単です。さらに、導出された相関行列を分解し、相関行列\(\bf =C∙C^⊤\) となるような行列 \(\bf C\) を導出すれば、2つの標準正規乱数から、\(I_{Δw}~と~Δw\) を生成する事ができます。\(Δw\) は、もともと MSC に必要な正規乱数であり、従って乱数をもう1個追加するだけです。
Glasserman本では、この \(I_{Δw}\) を、シミュレーションではなく、期待値で求める方法も提示されています。上記の図から判る通り、\(I_{Δw}\) は、底辺がh、高さがΔwの直角三角形の面積に近いであろうことが推察されます。実際に \(E(I_{Δw} )=\frac 1 2 Δw\) であり、その三角形の面積が \(I_{Δw}\) の期待値になります。そこで、\(I_{Δw}\) を、今説明したシミュレーションではなく、この期待値を使えば、正規乱数の生成は \(Δw\) だけで済み、より高速化できます。期待値を使っても、誤差のオーダーは \(o(h^2)\) です。
(5) 2次の離散近似スキーム
以上から、\(L_i(t+h)\) の2次のオーダーの離散近似スキームが、以下のように導出できます。シミュレーションに必要な乱数は \(Δw~ と~ I_{Δw}\) です。
\[ \begin{align} L_i(t+h) = & L_i(t) \\ & +ah+bΔw \\ & +(ab'+ \frac 1 2 b^2 b'')(Δwh-I_{Δw})+a'bI_{Δw} \\ & + \frac 1 2 bb'(Δw^2-h)+(aa'+ \frac 1 2 b^2 a'') \frac 1 2 h^2 \tag{6.120} \end{align} \]または、\(I_{Δw}\) のかわりに、その期待値である \(\frac 1 2 Δw\) を使えば、必要な乱数は \(Δw\) のみです。
実際にこの式を使ってシミュレーションする場合、まず \(a(t)~~ a'(t)~~a''(t),~~b(t)~~b'(t)~~b''(t)\) はすべて t 時の値を計算して使います。従って、\(a(t),~b(t)\) とも2階微分可能である事が前提です。それらの微分が解析的に求まれば、それを使いますが、求まらない場合は、差分を使います。
以上が、シングルファクターモデルにおける、2次のオーダーの離散近似スキームです。LMM のようなマルチファクターモデルでは、これが遥かに複雑になります。LMM の MCS では、このスキームではなく、次に説明する Richardson Extrapolation 法が使われる事が多いのではないかと思います。