実務で使える金融工学　上級編

上級編　６．　 Libor Market Model　

6.4  　フォワードLibor間の相関の構造

6.4.3   相関行列の補正

 

6.4.3.1   相関行列のスムーズ化

前のセクション6.4.2 で求めた Historical な相関行列 \(\bf R_H\) は、ノイズが多く含まれ、決して滑らかではありません。LMM では相関の情報を、将来のLibor金利の同時分布を求める為に使いますが、そういったノイズが将来にも続くと仮定するよりは、相関行列の特徴だけを押さえた滑らかなデータを使う方が、理にかなっていると思います。という事で、先ほど求めた相関行列を、滑らかな関数を使って、補正します。具体的には、関数形を決めて、そのパラメータを原データに Calibration します。関数形を決めるにあたっては、過去データから得られる相関行列の特徴を表現できるようなものを選びます。既に触れましたが、Libor 間の相関行列には、以下のような特徴がみられます。 

• Libor 間の相関は概ね正の値を取る
• 短期のテナーのLibor間では相関は低く、長期のテナー同士では高くなる傾向
• Libor のテナーが離れるにつれて、相関は低下していく

さらに、３点目について、Andersen-Piterbarg本では、次のような特徴を指摘しています。 

• Liborのテナーが離れるにつれて相関は低下していくが、低下の度合いは、最初は指数関数的に急激で、遠くなるにつれ、緩やかになる。

そういった関数形について、様々な文献で提案がなされていますが、その中から　Andersen-Piterbarg の提示している関数形を紹介します。Andersen-Piterbarg は、上記のような特徴を持つ相関行列を、パラメトリックな指数関数で表現しています。（Andersen-Piterbarg“Interest Rate Modeling”　Section 14.3.1） 

相関行列の各要素となる、\(L_i~~と~~L_j\) の瞬間相関係数を、それぞれの Libor の残存期間 \(（T_i-t=x,~~T_j-t=y）\) を変数とする指数関数で表現しています。 

\[ \begin{align} q_1(x,y) &=ρ_∞ + (1-ρ_∞) \exp\left(-a(\min(x,y))~|y-x|\right),~~~~1 > ρ_∞ > 0 ~~~~~~~~~~~\\ & where ~~~~~a(\min(x,y))=a_∞ + (a_0-a_∞) e^{-\kappa ( \min(x,y))},~~~~\\ & ~~~~~~~~~~~~~~~~ a_0 > a_∞ > 0,~~~~~\kappa > 0 \tag{6.55} \end{align} \]

上の1行目の式は、\(|y-x|\) が 0 、すなわち同じ Libor 間の場合、相関は 1 となり、\(|y-x|\) が大きくなるにつれ減衰してゆき、\(\rho_∞~~ (但し 1 > \rho_∞ > 0~)\) に近づいていきます。また、その減衰のスピードである \(a(\min(x,y))\) は、２行目の式にある通り、２つの Libor の残存期間の短い方に依存し、それが大きくなるにつれ、減衰のスピードは弱くなっていきます。 

Andersen-Piterbarg は、6.50 式でも、過去データの相関行列にフィットさせるのに、十分な自由度があると述べていますが、さらにもう少し自由度を上げた下記のような式も提示しています。この式が意図するのは、フォワード Libor のテナー間の距離　\(|y-x|\) の、無限遠での収束ポイントである \(\rho_∞\) について、Libor のテナーが長くなるにつれ、少しずつ大きくしていこうとするものです。 

\[ \begin{align} q_2(x,y) & =ρ_∞ ( \min(x,y))+ (1-ρ_∞ ( \min(x,y) ))~ \exp \left(-a(\min⁡(x,y) )~|y-x|\right) \\ & where ~~~~~ ρ_∞ (\min⁡(x,y) )=b_∞+(b_0-b_∞ )~ \exp (-a~ \min(x,y)) \\ & ~~~~~~~~~~~~~ 1> b_∞ > b_0 > 0 \tag{6.56} \end{align} \]

こうする事によって、ｑ２は、ｑ１と比較して、長期のテナーのＬｉｂｏｒ間の相関が、より強くなるように表現できます。このように、スムーズ化した Historical な相関行列を、以下　\(\bf \tilde R_H\) と表記します。 

 

<  スムーズ化した相関行列が正定値行列にならなかった場合  >

6.55 や 6.56 式などのスムーズ化関数を使って修正した相関行列　\(\bf \tilde R_H\)　は、稀にですが、正定値行列とならず、マイナスの固有値が出現するケースがあります。その場合、それを修正して、できるだけ元の行列に近い形の正定値行列に変換します。経験的には、マイナスの固有値は発生しても僅かであり、それを修正しても、行列の作用素としての働きの効果はほとんど維持されます。 

その修正のアルゴリズムは、修正後の正定値行列となる相関行列を　\(\bf \tilde R_H^*\) とすると、（たまたま正定値でない）相関行列 \(\bf \tilde R_H\) との誤差のフロベニウスノルムが最小となるように、Solver を使って求めます。具体的なアルゴリズムは Higham（“Computing the nearest correlation matrix”2002）が提示しているので、それを参考にして下さい。 

負となる固有値が十分小さい場合、次のような簡易な方法でも正定値相関行列を求める事ができます。まず、過去データから導出された分散共分散行列を B とします。そして、その B を固有値分解します。 

\[ \bf B=E∙Λ∙E^{\top} \]

但し、Λ は、その対角要素が B の固有値となる対角行列で、E は、各固有値に対応する固有ベクトルを縦ベクトルとして並べた行列です。 

仮に Λ の対角要素のいくつかが、負の値であった場合、それを　0　に限りなく近い、微小な実数εにおきかえ、新たな対角行列　\( \bf Λ^*\) を作ります。数式で表すと、下記のような操作になります。 

\[ Λ_{i,i}^*= \max (ϵ,Λ_{i,i}),~~~~~~ i=1,2,…,m \tag {6.57} \]

そして、この新たな対角行列 \(\bf Λ^*\) に、固有ベクトル行列 E を左右から作用させ、新たな分散共分散行列 \(\bf B^*\) をつくります。 

\[ {\bf B^* = E∙Λ^*∙E^{\top} } \tag{6.58} \]

\(\bf B^*\) から、その各対角成分の平方根を取って、新たな対角行列　\(\bf V^*\) を作り、\(\bf B^*\) と\(\bf V^*\) から下記のような操作で、新たな相関行列　\(\bf \tilde R_H^*\)　を導出します。 

\[ {\bf \tilde R_H^*=(V^*)^{-1} B^* (V^*)^{-1} } \tag{6.59} \]

こうして導出された \(\bf \tilde R_H^*\) は、正定値行列で、かつその対角要素はすべて 1 になり、有効な相関行列になります。 

 

6.4.3.2   相関行列のランクダウン

次に、スムーズ化した相関行列　\(\bf \tilde R_H\) （あるいは、さらに若干修正した \(\bf \tilde R_H^*\)） を、LMM のブラウン運動の次元数に下げる為、ランクダウンした行列　\(\bf ρ =C∙C^{\top}\) で近似します。(ρは n × n　次の行列だがランクは m 以下、C は　n × m 次の行列) 。その方法はいくつかありますが、Andersen-Piterbarg が紹介している２通りの方法を解説します。 

6.4.3.2.1　  PCA を使った行列の低ランク近似 

PCA（Principal Component Analysis:主成分分析）を使って、与えられた行列から、ランクを下げた近似行列を導出する方法は、広く知られています。与えられた ｎ × ｎ 次でランク ｎ の正方行列を \(\bf \tilde R_H\) とし、それを同じ次数ではあるものの、ランクを m （m < n) に下げた行列で近似する場合、次のような最小値問題として捉える事ができます。 

\[ {\bf ρ}=\min_{\rm X∈R^{n×n}}‖{\bf \tilde R_H-X}‖_F, ~~~~~~~ {\rm rank({\bf ρ}) \leq m } \tag{6.60} \]

但し、\(‖{\bf \tilde R_H-X}‖_F\) は、解行列 X とターゲット行列 \(\bf \tilde R_H\) との誤差のフロベニウスノルムです。そして、この ρ は、もし何の制約条件もなければ、次のように \(\bf \tilde R_H\) を 固有値と固有ベクトルに分解した行列から簡単に求める事ができます。 

\[ \begin{align} \bf \tilde R_H & = E∙\Lambda∙ E^{\top} \\ \bf ρ & = E_m ∙ \Lambda_m ∙ E_m^{\top} \tag{6.61} \end{align} \]

但し 

• \(\bf \Lambda ~~~:~~\tilde R_H \) の固有値を絶対値の大きい順に対角成分に並べたｎ次の対角行列。
• \(\bf \Lambda_m ~:~~\tilde R_H \) の固有値の内、絶対値の大きい順に ｍ 個並べたベクトルを対角成分に持つ ｍ 次の正方行列
• \(\bf E ~~~~:~~\tilde R_H \) の各固有値に対応する固有ベクトルを縦ベクトルとしてならべた ｎ × ｎ 次の行列。
• \(\bf E_m ~:~~\Lambda_m \) に対応する固有ベクトルを縦ベクトルとして、ｍ個並べた ｎ × ｍ 次の行列

ところが、求めるべき低ランク近似行列 ρ は、Libor の相関行列としての要件を満たす必要があり、正定値行列でかつ対角成分がすべて 1 でなければなりません。この内、正定値行列の要件は、\(\bf \tilde R_H\) が正定値行列であれば、低ランク近似した行列も正定値になることが証明されています。（その証明は省略します）　一方、対角成分については、6.61 式の低ランク近似を行った場合、すべて 1 になる保障は全くありません。そこで、そのような制約条件をかけた下記の最小値問題を解く必要があります。 

\[ {\bf ρ = \min_{X∈R^{n×n}}‖\tilde R_H-X‖_F} ~~~~~ subject~~to~~ {\bf v(ρ)-I=0 } \tag{6.62} \]

但し ρ は最適化された X で、上記式の解となる行列。v(ρ) は、行列 ρ の対角成分のベクトルで、Ｉ と ０ はすべての要素がそれぞれ 1 と 0 のベクトル。 

この制約条件付きの行列の低ランク近似問題は、先ほどの　PCA　による上位　ｍ　個の固有値と固有ベクトルを使った方法では解けません。また、これをそのまま、Solver　にかけたとしても、相関行列の次数と、その対角成分の要素数（80～160）を考えると、相当時間がかかるか、場合によっては収束しない可能性もあります。 

そこで、Andersen-Piterbarg　本では、Zhang-Wu（“Optimal low-rank approximation to a correlation matrix”2003）の方法を紹介しています。以下にその概要を解説します。そのエッセンスは、制約条件付き最小値（または最大値）問題を、ラグランジュの未定乗数法を使って min-max 問題に変換し、それを数値的に解くものです。ラグランジュ関数に最小値（あるいは最大値）が存在し、かつそれが一意である為の条件や、その証明のプロセスの説明は私の手に負えません。きちんと理解されたい方は、上記の原典の論文を参考にして下さい。 

では、その方法です。まず、6.62 式の制約条件付き最小値問題を、ラグランジェ関数を使って同値な min-max 問題に変形します。まずラグランジェ関数を次のように定義します。 

\[ L({\bf X,d})=-‖ {\bf \tilde R_H-X} ‖_F^2 - 2 {\bf d∙diag( \tilde R_H-X)} \tag{6.63} \]

但し、第1項（ターゲット行列 \(\bf \tilde R_H\) と、求めるべき解の行列 X の誤差）の符号が − になっているので、このラグランジェ関数は、最小値ではなく最大値問題になります。また右辺の第2項のベクトル ｄ は、ラグランジュ乗数ですが、それを任意の値でとれるので（ｄ を ∞ にすれば、右辺はいくらでも大きくできるので）、右辺の第2項が 0、すなわち \(\bf diag(\tilde R_H-X)=0\) でない限り 6.58 式に最大値は存在しません。すると、第2項＝0 は、6.57 式の制約条件と同値である事を意味します。その中で第1項の最大値、すなわちターゲット行列 \(\bf \tilde R_H\) に出来るだけ近い X を求めます。 

そして、この関数を使って、6.63 式と同値な min-max 問題を解きます。 

\[ \min_d \max_{\bf X∈R^{n×n}}L(X,d) ~~~~~~~ rank( {\bf X} ) \leq m \ll n \tag{6.64} \]

その解き方は、まず \(\max_{ \bf X∈R^{n×n}}L({\bf X,d} )\) を満たす d を求める関数を 

\[ V({\bf d}) = \max_{{\bf X∈R^{n×n}}}L({\bf X,d}) \tag{6.65} \]

とおき、その d の集合の中から、\(\min_d⁡V(\bf d)\) を求める操作を行います。 

\[ {\bf d^*}= \min_d V({\bf d}) \tag{6.66} \]

最終的の、6.65 と 6.66 を満たす X が、求めるべきランクダウンされた相関行列になります。ただ、このままでは、具体的な数値解析プロセスがまだ見えません。 

そこで、Zhang-Wu は、6.63 式のラグランジェ関数を変形し、下記式と同値である事を示しました。（証明のプロセスは、原典をご覧ください。） 

\[ L({\bf X,d})=-‖{\bf \tilde R_H+D-X}‖_F^2+‖{\bf d}‖_2^2 \tag{6.67} \]

但し、行列 D は、ベクトル d を対角要素に持つ対角行列です。この式は、ターゲットを \(\bf [ \tilde R_H+D]\) とした制約条件なしの低ランク近似問題をラグランジェ関数にしたものであり、最初に示した 6.57 式と同じとみなせます。6.57 式の解は、ターゲット行列を固有値分解すれば簡単に求まるのでした。従って、6.64式も、まず最初に任意のベクトル　d　を決めてやれば、固有値分解で、その d に対応する最適解 X が求まります。 

　そこで \([ \bf \tilde R_H+D]\) の固有値分解が下記のように求まったとします。 

\[ {\bf [ \tilde R_H+D]= \hat E∙ \hat Λ∙ \hat E^{\top} } \tag{6.68} \]

すると、左辺の行列をランク ｍ に落とした近似行列 ρ は、6.58 式から 

\[ {\bf ρ= \hat E_m ∙ \hat Λ_m ∙ \hat E_m^{\top} } \tag{6.69} \]

として求まります。この ρ は与えられたベクトルｄの対角行列 D に依存するので、d に依存する関数として ρ(d) と表記できます。そして、その対角成分が 1 になるような制約条件は 

\[ {\bf v(ρ(d))-I=0 } \tag{6.70} \]

となりますが、これが成立するように、d を少しずつ動かして6.70 式が成立するような d を求めればいいことになります。 

繰り返して言うと、まず任意の d を与え、それをもとに 6.68 と 6.69 式から低ランク近似行列 ρ(d) を求めます。そして、それが 6.70 の 条件を満たしているかチェックします。満たしていなければ、ベクトル ｄ の値を動かし、同じプロセスを繰り返します。最終的に 6.70 を満たす ｄ（それを d* とします）が見つかれば　\(\bf ρ(d^*) \) が求めようとしている低ランク近似された相関行列になります。さらにそれを 

\[ \bf ρ(d^*)=C∙C^{\top} \]

と分解して得られた行列 C (n × m　次)　が、LMM　の拡散項係数の相関ファクターになります。 

 

6.4.3.2.2   より簡便な相関行列の低ランク近似 

Andersen-Piterbarg 本では、上のセクションで紹介した Zhang-Wu の方法以外にも、以下のような、より簡便な方法での相関行列の低ランク近似方法を紹介しています。（Section 14.3.4.2　Poor Man’s Correlation PCA） 

まず、ターゲットとなる相関行列（セクション 6.4.2 の過去データから求めた相関行列を、さらにスムーズ化した行列） \(\bf \tilde R_H\) を固有値分解し、そこから上位 ｍ 個の固有値と固有ベクトルから、以下のような行列を生成します。それを示した 6.61式を再記します。 

\[ { \bf \tilde R_H=E∙Λ∙E^⊤ \\ \bf ρ=E_m∙Λ_m∙E_m^{\top} } \tag{6.61} \]

すでに述べたように、元の相関行列を、制約条件なしで低ランク近似した上記の行列 ρ は、対角要素が 1 になるとは限らず、そのままでは相関行列として使えません。 

そこで、まず、6.61 で求めた ρ の対角成分だけを取り出し、それの平方根を対角要素に持つ対角行列 \(\bf [r_m]\)を作ります。ρ の対角成分を \(ρ_{i,i},~~~i=1,2,…,n\) とすると、 

\[ {\bf [r_m ]}=\left[ \begin{align} \sqrt {ρ_{1,1}} & ~~~~~~~~~0 & 0~~~~ \\ 0~~~ & ~~~~~~~~~\ddots & 0~~~~ \\ 0~~~ & ~~~~~~~~~0 & \sqrt {ρ_{n,n}} \end{align} \right] \]

そして、この \(\bf [r_m]\) の逆行列を ρ の左右から掛けます。そのようにして生成された新たな行列を　\(\bf ρ^*\) とおきます。 

\[ {\bf ρ^*=r_m^{-1} ∙ ρ ∙ r_m^{-1} } \tag{6.71} \]

この操作は、行列 ρ の全要素をその対角成分で正規化した事になり、その結果 \(\bf ρ^*\) の対角成分はすべて 1 となり、相関行列の要件を満たします。 

さらに、\(\bf ρ^*\) を分解した ｎ × ｍ 次の行列 Ｃ も、以下の式で簡単に求まります。 

\[ {\bf ρ^*=C∙C^{\top} \\ C=r_m^{-1}∙E_m∙ \sqrt {Λ_m} } \tag{6.72} \]

 

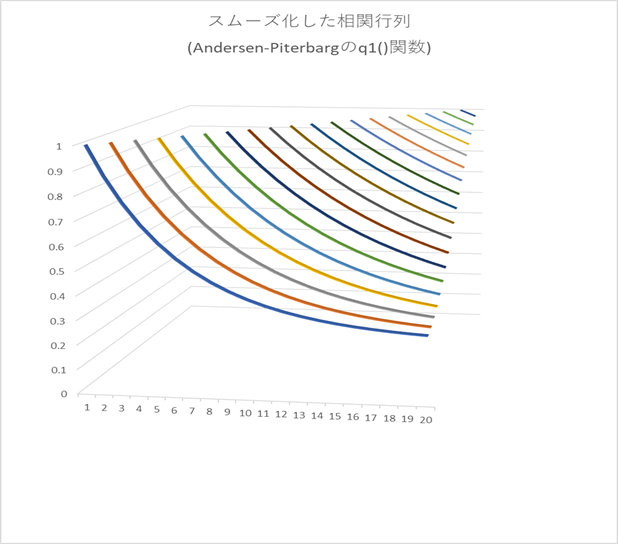
6.4.4   導出された相関行列のイメージ

 

以上のようなプロセスを経て得られた相関行列を、グラフでイメージすると下記のような感じです。（実際のデータではなく、あくまでイメージをつかむ為のテストデータです。）