実務で使える金融工学　上級編

上級編　６．　 Libor Market Model　

6.1.2   同値マルチンゲール測度と測度変換の公式

6.1.2.3  測度変換の公式の導出

さて、LMM のように、複数の確率変数の同時分布を考える必要がある場合を考えてみます。ここでも、「すべての金融商品について、その価格変動を Replicate（複製）できる取引戦略が存在している」という条件が大前提です。通常、Payoff が複数の Libor に依存するデリバティブズのリスクを消すには、まずデリバティブズ価格の各 Libor への感応度に応じてリスクを消します。金利デリバティブズでは、通常、Libor のスタート日とエンド日がキャッシュフロー発生日になり、各 Libor への価格感応度をもとに、その日が満期のゼロクーポン債を使ってリスクヘッジを行います。 

Libor ごとのリスクはこれで完全にヘッジされ、その Libor は、エンド日を満期日とするゼロクーポン債をニュメレールにした確率測度下で、マルチンゲールになります。しかし、デリバティブズ価格が、複数の Libor の同時分布に依存する場合、価格評価（すなわち期待値演算）に使う確率測度（すなわち、その基準となるニュメレール）はひとつに特定しなければなりません。その為には、各 Libor と対応するニュメレールとの相対価格自体をさらに、期待値演算で使う確率測度に対応する別のニュメレールに Replicate しなければなりません。すなわち、ニュメレール同士の相対価格の確率過程も考える必要があります。その際、ニュメレール間の相関が 0（すなわちそれぞれ独立）であれば、問題は簡単です。一つの確率測度の同時分布を考える場合でも、ニュメレール毎の確率測度がそのまま使えます。その場合、各測度下でマルチンゲールなので、ドリフト項を考える必要はありません。しかし、一定の相関がある場合、僅かですがドリフト項の調整が必要になります。 

初期のLMMの文献は、その調整方法の解説がメインになっています。人によっては、それらの論文はLMMを新たなモデルとして提示したのではなく、「市場がアービトラージフリーの場合における、ドリフト項の調整方法」を提示しただけとの意見もあります（Rebonato-Mckay-White“the SABR/LIBOR Market Model”）。（注：フォワードLiborが幾何ブラウン運動するモデルは、BGMやJamishidianの論文以前に、すでにBlackモデルが紹介された当時からありました。）　いずれにしても、その調整項を導出する必要があるので、以下にその解析プロセスを解説します。プロセスは大まかに、以下のような手順になります。 

1. 対象資産と 2 種類のニュメレールを含む証券市場全体の SDE を定義
2. ２つの同値な確率測度間の換算係数：ラドン・ニコディム微分の定義
3. ラドン・ニコディム微分の確率過程の導出：ニュメレールの相対価格から
4. ラドン・ニコディム微分の確率過程の導出：ギルザノフの定理から
5. 上記３，４，の２つのラドン・ニコディム微分が一致する事から、測度変換の公式を導出

 

6.1.2.3.1  証券市場全体の確率過程

複数の証券価格の同時分布を使うので、まずｎ個の資産からなる証券市場を考えます。 

（以下、多次元の確率変数を取り扱うので、スカラ、ベクトル、行列の表記を、スカラは細字(a,b,t,x,y,X,Y,N,M,α,β,σ,など)、ベクトルは小文字の太字（x,y,α,β,σ,ωなど)、行列は大文字の太字上（X,Y,Α,Β,Σ,）を極力使うようにします。） 

その市場における t 時の証券価格を \( {\bf x(t)}= \{ x_1 (t),x_2 (t),…,x_n (t) \} \) とベクトル表記します。そして、それらが ｎ 個の独立したブラウン運動 \( {\bf w(t)} = \{ w_1 (t),w_2 (t),…,w_n (t)\} \) で駆動されるとします。また各証券 \({x_1 (t),x_2 (t),…,x_n (t)}\)　の確率変動は互いに相関を持ち、その相関係数は、\(n~×~n\) の行列 ρ で与えられるとします。さらに行列 ρ の平方根に相当する行列を C と表記します。すなわち \({\bf ρ=C∙C^{\top }} \) となります。この C は、x(t) の確率過程を記述する SDE の拡散項係数に登場し、n 次元ブラウン運動に作用します。 

証券価格 x(t) はブラウン運動 w(t) により生成される確率空間 \( \{Ω,F_t,P\}\) 上の確率過程で、P は自然な確率測度とします。またこの確率空間は、ゼロ測度の事象で補完され、いわゆる usual condition（適切な日本語訳が判らないので、英語のまま使っています。）を満たすとします。 

ここで、x(t)はマイナスの値を取る事はなく、かつ事象の観測期間 [0,T] 間において、クーポンや配当を支払う事もないとします。具体的には Libor のテナー構造に満期日をもつゼロクーポン債価格の集合を想定すればいいでしょう。それらがすべてデフォールトリスクの無いゼロクーポン債であれば、いずれもニュメレールになり得ます。そして、それらの証券が、以下の確率過程を取るとします。 

\[ {\bf dx(t)=μ^P (t,x(t))}dt+{\bf Σ(t,x(t))∙C∙dw^P(t) } \tag{6.3} \]

但し 

• \( {\bf μ^P (t,x(t))}\) ： P 測度下でのドリフト項係数で n 次元のベクトル。
• \( {\bf Σ(t,x(t))} \) ： 各証券価格の確率過程における拡散項係数に相当する \(ｎ~×~ｎ\) の対角行列。対角要素 \( σ_i (t,x_i (t)) \) は、\(\scr F_t\) に適合した Deterministic な関数とする（ここではStochastic Volatilityは考えない）。
• \( \bf C\) ： X の相関行列 ρ を分解した行列。すなわち \( \bf ρ=C∙C^{\top }\) を満たす C
• \( \bf w^P\) ： 自然な確率測度 P 下での、n 次元の独立なブラウン運動。

(3)式は、個別の証券のSDEに分解すると、 

\[ dx_i=μ_i^P(t,x_i (t))dt+{\bf σ_i (t,x_i (t))∙C∙dw^P }(t)~~~~~i=1,2,…,n~~~~~~~~~~ (6.3)' \]

という形の連立 SDE となります。 \( \bf σ_i (t,x_i (t))\) は、(6.3)式にある対角行列 Σ の i 行目のベクトルで i 番目の要素以外は 0 となります。すなわち、 \( \bf \sigma _i (t,x_i(t)) =\rm \{ 0,…,\sigma _i (t,x_i ), … ,0 \} \)  

以下、解析を進める上で必要な数学的な設定や前提条件は、すべて満たしているとします （　ｘ　は　2　乗可積分、μ、σ　はリプシッツ条件や成長条件を満たすなど。クオンツの文献の至る所で登場するので、説明は省略します）。x は証券価格のベクトルになるので、負の値を取る事は無く、すると拡散項係数を　\( σ_i (t,x_i )=σ_i (t) x_i\) として、幾何ブラウン運動する確率変数と考えた方が自然ですが、とりあえず関数形を特定せず \(σ_i (t,x_i )\) としておきます。 

 

6.1.2.3.2  同値な確率測度間の測度変換係数（ラドン・ニコディム微分）

２つのニュメレールを M(t), N(t) とします。いずれも x の中のどれかに該当、すなわち M(t),N(t)∈x とします。また、そのニュメレールに対応する同値マルチンゲール測度をそれぞれ \(Q_M,~Q_N\) と表記します。すると、ある証券の価格 S(t)∈x　について、次の２つのマルチンゲール式が成立します。 

\[ \frac{S(0)}{M(0)}=E^{Q_M} \left[ \frac{S(t)}{M(t)} ~|~ \scr F _0 \right],~~~~~~ \frac{S(0)}{N(0)}=E^{Q_N} \left[ \frac{S(t)}{N(t)} ~|~ \scr F _0 \right] \tag{6.4} \]

証券市場は、一物一価なので、２つの式の S(0) は一致します。すると、上の２つの式から下記等式が導けます。 

\[ M(0) E^{Q_M} \left[ \frac{S(t)}{M(t)} ~|~ \scr F_0 \right] = N(0) E^{Q_N} \left[ \frac{S(t)}{N(t)}~|~\scr F_0 \right] \] \[ or~~~E^{Q_N} \left[ \frac{S(t)}{N(t)}~|~\scr F_0 \right] ~~~~~~ =E^{Q_M} \left[ \frac {S(t)}{N(t)} ∙ \frac{N(t)}{M(t)}\frac{M(0)}{N(0)}~|~\scr F_0 \right] \tag{6.5} \]

ここで、右辺の期待値演算の中にある \( \frac{N(t)}{M(t)} \frac{M(0)}{N(0)}~~ を~~ ζ(t)\) と置き、(6.5)式を若干書き換えます。 

\[ E^{Q_N} \left[ \frac{S(t)}{N(t)}~|~\scr F_0 \right] =E^{Q_M} \left[ \frac {S(t)}{N(t)} ∙ \zeta (t)~|~\scr F_0 \right] ~~~~~~~~~~~~~~~~~(6.5)' \]

さらに、これを積分形で表現すると下記のようになります。 

\[ \int \frac{S(t)}{N(t)} dQ_N (t)=\int \frac{S(t)}{N(t)} ζ(t)dQ_M(t) ~~~~~~~~~~~~~~~~~~~ (6.5)'' \]

ここから \(dQ_N (t)=ζ(t)dQ_M (t),~~~or~~~ \frac{dQ_N (t)}{dQ_M (t)}=ζ(t) \) という関係が導けます。気づかれたと思いますが、ζ(t) すなわち \( \frac{N(t)}{M(t)} \frac{M(0)}{N(0)}~~~は~Q_M~ 測度から~Q_N~ \)測度へ変換する為のラドン・ニコディム微分に相当します。 

 

<  ラドン・ニコディム微分  >

ここで、寄り道をしてラドン・ニコディム微分について、ある程度直観で理解できるような解説を試みます。まず、以下の命題があります。 

「同値な確率測度の間には、一意の変換係数が存在し、その変換係数を使えば、ある確率測度から別の確率測度への変換が可能」 

いわゆるラドン・ニコディムの定理です。その変換係数をラドン・ニコディム微分（Radon-Nikodym Derivative）と呼びます。このラドン・ニコディム微分の定義は、ある事象空間 \(\{Ω,F,∙ \}\)上で定義された２つの確率測度 P と Q について、下記のような条件を満たす \( dQ/dP\) になります。 

\[ dQ(A)=\int _A \frac{dQ}{dP}dP ~~~~∀~A∈Ω　　　\\ 但し~~~~dP(A)=0~~~なら~~~dQ(A)=0 \]

また、ラドン・ニコディム微分は、初期値は 1 で期待値が 1 の指数マルチンゲールとなる確率変数である事が知られています。なぜそうなるかの数学的な説明については、私の手に負えません。(おそらく、正規分布間のラドン・ニコディム微分はそうでしょうが、他の確率分布でどうなるかよく分かりません。)　数学の専門家により解説された文献が多数あるので、そちらをご覧ください。ここでは、数学的厳密さよりは、直観で理解できるような解説を試みたいと思います。 

クオンツファイナンスの世界では、同値な確率測度（同値マルチンゲール測度）は、自然な確率分布を、その分布形状を維持したまま平均をずらしたものに相当します。数学的には、もっと深い意味、例えば分布形状が異なる確率測度間でも定義できるかも知れませんが、クオンツファイナンスの世界ではこの理解で十分です。例えば、ある証券S(t)について、スポット価格のＴ時の分布と、T時のフォワード価格の分布を比べたのが、そうなります。グラフで表せば、下記のような関係になります。分布の形状は相似ですが、平均値の位置がずれています。 

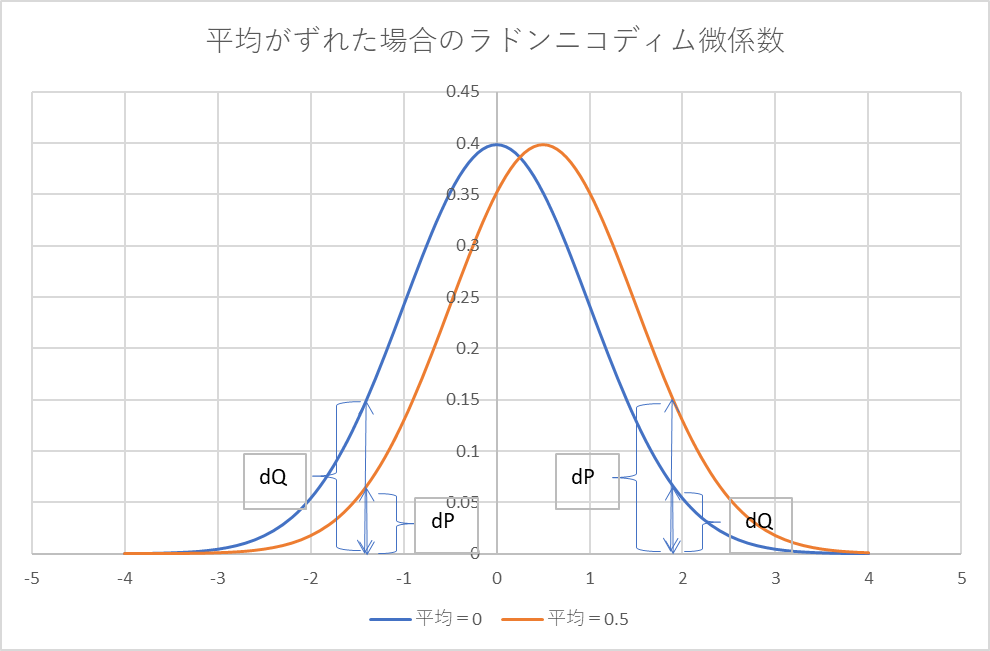
上の２つのグラフは正規分布の密度関数で、これを −∞ から ＋∞ まで積分すれば 1 になります。ラドン・ニコディム微分は、各点における確率密度の比率になります。その比率は、グラフを見て判る通り、1 より大きかったり小さかったりするものの、その平均（期待値。すなわち −∞ から ＋∞ まで積分した値）は 1 になりそうだというのは、感覚的に理解できるのではないでしょうか。 

この確率分布のずれは、確率分布を観測する基準点をずらすことによって生じます。ある証券が自然な確率測度の下で、\(μ^P(t)dt\) の比率でドリフトしながら、ランダムに拡散していくとします。その証券の一定時間後の確率分布を、リスクフリー金利のリターンを持つ預金口座を基準に観察する場合、本来の確率分布から　 

\[ \int _0^T μ^P(t)dt~-~\int _0^T r(t)dt \]

だけずれた確率分布が観測されます。それが上のようなグラフになります。 

この２つの確率分布は、ドリフト項の差分だけ時間の経過とともに、ずれ（平均の差）が大きくなっていきます。また分布の幅（分散）は経過時間に比例して大きくなり、山の形状が次第になだらかになっていきます。各点におけるラドン・ニコディム微分も、時間の経過に合わせて変化していくのは、簡単に想像がつくでしょう。すなわち、ラドン・ニコディム微分も同じ確率空間上で確率過程を取るという事です。また逆に時間を遡っていけば、ｔ＝0 では、両者の確率分布は一致（現在の証券価格なので、確率 1 で一点に確定）します。すると、ラドン・ニコディム微分の初期値が 1 になるのも容易に推察できると思います。ラドン・ニコディム微分が、初期値が 1 の指数マルチンゲールになるというのは、こういう事です。 

いずれにしても、同じ事象空間上に複数の確率測度が想定できる場合、ラドン・ニコディム微分を使って確率測度の変換ができる訳です。 

 

それましたが、もとに戻ります。 

ある証券 S(t) のニュメレールとの相対価格は、そのニュメレールを基準とする確率測度下でマルチンゲールになるのでした。それは異なるニュメレールを基準にした同値マルチンゲール測度でも成立します。そこから、(6.5)式 を導出しました。その式から、\(Q_M\) 確率測度から \(Q_N\) 確率測度へ変換するラドン・ニコディム微分 \( \frac{dQ_N}{dQ_M} \) が、下記のようにニュメレールの相対価格に一致する事が判りました。 

\[ ζ(t)=\frac{dQ_N}{dQ_M}= \frac{N(t)}{M(t)} \frac {M(0)}{N(0)} \tag{6.6} \]

若干書き換えると 

\[ \frac{N(t)}{M(t)} \frac {M(0)}{N(0)}= \frac{N(t)}{M(t)}÷\frac{N(0)}{M(0)}= \frac {t~時のニュメレール相対価格}{現在のニュメレール相対価格} \]

すなわち、ラドン・ニコディム微分は、現在のニュメレールの相対価格を基準にした、将来( t 時)の相対価格に相当します。ラドン・ニコディム微分も幾何ブラウン運動する確率変数なので、その SDE の形を求めてみます。(6)式の両辺を微分すると 

\[ dζ(t)=\frac {M(0)}{N(0)} d \frac{N(t)}{M(t)} \tag{6.7} \]

右辺の N(t)/M(t) は、M をニュメレールとした相対価格なので、\(Q_M\) 測度下でマルチンゲールになります。N(t) と M(t) の SDE の形が判れば、 \(d \frac {N(t)}{M(t)} \) の SDE も、求まり、その結果、ラドン・ニコディム微分 \(d\zeta (t)\) の確率過程（SDE）も求まります。 

次のページで、このニュメレールの相対価格の確率過程を求めていきます。