上級編 6. Libor Market Model
6.6 モンテカルロシミュレーション
6.6.6 アメリカンタイプのオプションへの対応(続き)
6.6.6.3 Parametric Stopping Rule
6.6.6.3.1 行使境界曲線
アメリカンタイプのオプションを価格評価する際のベースになる考え方は、期限前行使日において「行使価値と継続保有価値を比較して高い方を選択する」というものでした。それを数式にしたのが、6.126 式です。
\[ V_i(x_i)=\max \left(h_i(x_i),~c_i(x_i)\right) = \max\left( h_i(x_i),~E\left[V_{i+1}(x_{i+1})|x_i\right] \right) \tag{6.126} \]この考え方を、別角度から見た考え方として、「期限前行使の最適なタイミングを探す」という方法があります。max 関数を評価するために、上の式では、継続保有価値を求めていましたが、行使するかどうかの判断だけであれば、\(h_i(x_i)=c_i(x_i)\) となっているラインが判れば十分です。確率変数がそのラインを越えれば行使すればいい訳ですから。そのラインを行使境界曲線と呼びます。それをパラメトリックな関数で近似する方法が、Parametric Stopping Ruleと呼ばれるテクニックです。その考え方は次のようなものです。
アメリカンタイプのオプションで、そのオプション行使が可能なタイミングの集合を \(\mathcal {T}∈(0,T_M]\) とし、実際にオプション行使するタイミングを \(\tau\)、その時の確率変数の値を \(x_τ\) とします。さらに、その時のオプションの行使価値(ニュメレールで基準化された Payoff 関数)を \(h(x_τ)\) とすると、「期限前行使の最適なタイミングを探す」とは、下記式を満たすような \(\tau\) を探すことになります。( \(E^{Q_N}[~~]\) は N をニュメレールとした確率測度下での期待値演算)
\[ \sup_{τ∈\mathcal{T}} E^{Q_N} \left[h(x_τ)\right] \tag{6.129} \]\(\tau\) は確率過程 \(x(t)\) の停止時間になるので、\(x(t)\) の一定の範囲、すなわちオプションの期限前行使をすべき領域を特定します。確率過程 \(x(t)\) が最初にその領域に到達した時点で停止条件が成就する(=オプションを行使する)事になります。\(x_τ\) が示す領域は、行使価値が継続保有価値を上回るような \(x\) の領域になります。そのような \(x\) の領域を
\[ A=\{ x(t):h(x(t))≥c(x(t))\} \tag{6.130} \]とします。すると、\(\tau~~は~x(t)\) が最初にそこに到達した時刻になります。
\[ τ=\inf \{t \gt 0~:~x(t)∈A\} \tag{6.131} \]オプションの行使領域 \(A\) と、継続保有領域 \(A^c\) の境界は、例えば、シングルファクターの対象資産で、行使価格 100 のアメリカンタイプのコールオプションであれば下記グラフのような形状をしていると推察されるでしょう。
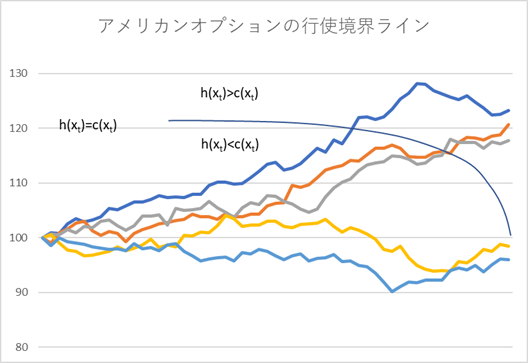
ここで、大胆な仮定をします。上記グラフにある、行使境界ラインは、\(h_t(x_t)=c_t (x_t)\) となる曲線ですが、それを何等かの関数 \(b^*(t)\) で仮定(近似)し、サンプル経路が最初にその境界ラインを越えたタイミング、すなわち \(h_t (x_t)≥b^*(x_t)\) となる t を \(\tau\)(すなわち期限前行使戦略)と見做すものです。式で表すと、下記のような \(\tau\) になります。
\[ τ^*=\inf\{t:h(x_t) \gt b^*(t)\} \tag{132} \]\(b^*(t)\) の関数形は、商品性の分析から "heuristic" に決めます。( heuristic の適切な日本語訳が思いつかないので、英語のままで使います。ここでの意味合いは、商品特性をよく分析した上で、関数の形状がどのようになるか推定し、その形に近そうな関数形を適当に決めるといった所です。関数の話の文脈で使われているので、analytic(解析的)と反対の意味になります。) そして、その関数の係数パラメータを、シミュレーションされたサンプル経路を使い、Optimizer を使って最適化問題を解く形で求めます。
この関数形 \(b^*(t)\) の決め方ですが、Glasserman 本などで解説されている方法は、極めてシンプルな関数形を想定して決めています。すなわち、上のグラフの境界曲線を、1 本の直線あるいは、複数の直線を繋げて近似するイメージです。具体的には、境界線を、ストライク価格からの距離で表現し、それを時間に対する単純な 1次関数(の組み合わせ)と仮定します。例えば、ストライク価格を K とすると、境界曲線 \(b^*(t)\) を下記式の ように仮定します。
\[ b^*(t)=a_i(T_{M-1}-t)+ K,~~~~a_i=\sum_{i=1}^{M-1} a_i I_{\{t_{i-1} \gt t \gt t_i\}} \tag{6.133} \](但し式中にある \(I_{\{t_{i-1}\gt t \gt t_i \}}\) は指示関数で、\(t_{i-1} \gt t \gt t_i\) の場合 1 を返し、それ以外の場合は 0 を返す)
グラフにすると、下記のグラフの赤のラインのようなイメージです。
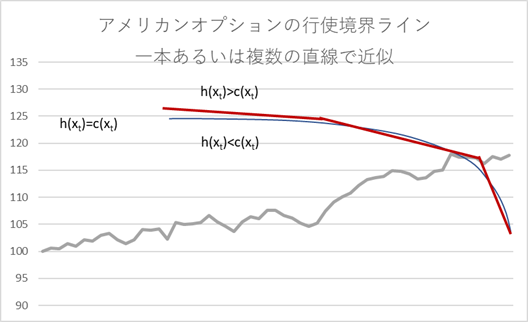
あるいは別の近似方法として、行使境界を、オプション行使日ごとに実数値のベクトルとして表現する方法もあります。
\[ {\bf b^*}=\{b_1,b_2,…,b_M=K\} \tag{6.134} \]( 但し、b の下付き文字はオプション行使日に対応するインデックス)
6.133 式(あるいは定数ベクトルの 6.134 式)が意味するのは、最終行使日 \(t=T_M\) における行使境界はストライク価格そのもので、そこから時間を遡るにつれ、行使境界は傾き \(a_i\) の直線に沿って In the Moneyの領域に方向に、次第に K から離れていくと仮定するものです。そして、この \(b^*\) の値を、サンプルを使って最適化問題を解く形で求めます。
かなりいい加減な方法のように見えますが、経験的には、これでもある程度精度の高い近似値が導出できる事が知られています。次のセクションでこの方法の具体的なアルゴリズムについて解説します。
6.6.6.3.2 行使境界曲線を求めるアルゴリズム
では、この方法のアルゴリズムを簡単に説明します。この方法は、前のセクションのグラフを見れば分かる通り、1ファクターの単純なアメリカンタイプのオプションでは、イメージしやすいでしょう。しかし、Payoff 関数が複数の確率変数に依存したり、プットとコールオプション(あるいは Payer と Receiver オプション)の両方の条件を持つようなオプションでは、行使境界曲線が、多次元の曲面になったり、複数(確率変数の上界と下界に)存在したりする事になり、簡単には定義できません。そういった場合は、商品特性、特に Payoff をよく分析して関数形を特定していく必要があります。ここでは、方法論の理解が目的なので、シンプルなバーミューダンスワップションを想定して、アルゴリズムを解説します。
- パラメトリックな関数形の特定 : まず行使境界曲線を近似する関数形を特定します。バーミューダンスワップションであれば、それを、行使日ごとの境界値のベクトル \(θ_i,~~i=1,…,M\) とするのが、適当かと思います。行使境界曲線を 1次関数で近似する場合でも、各行使日だけに着目すれば、同じような行使境界のベクトルになります。但し、スワップションの場合、各 \(θ_i\) はスワップ金利の水準になるので、サンプル経路がそこに到達したかどうか判断する為には、確率変数であるフォワード Libor のベクトルをスワップ金利に変換する必要があります。
- モデルに従った、フォワード Libor ベクトルのサンプル経路を \(m_1\) 個生成 : LMM の場合、フォワード Libor ベクトルのサンプル経路を、対象スワップの最終期日 \(T_E\) まで生成します。生成されたサンプルを \(x^{(i)},~i=1,…,m_1\) と表記します。そして生成されたサンプルからそれぞれ、\(T_M\) 時の対象スワップ金利 \(S_M (x^{(i)})\) を導出します(フォワード Libor ベクトル(すなわちフォワードLiborカーブ)からスワップ金利を導出する方法は、既に何度か説明しているので、ここでは説明しません)。
- 2.のサンプルを使って行使境界曲線パラメータ \(\theta\) (ここでは、関数ではなく行使日ごとに設定される値)を、\(θ_M\) から順番に時間を遡りながら、最適化問題を解く方法で求めます。まず、オプションの最終行使日 \(T_M\) における \(θ_M\) はストライク K に一致します。それを基準に、各サンプルの行使価値を求めます。
\[
h_M(x^{(i)})\cdot I_{\{S_M(x^{(i)})∈A_τ(θ_M)\}},~~~i=1,…,m_1 \tag{6.135}
\]
(上の式は満期Payoff関数と同じ意味です。)
但し、
- \(S_M(x^{(i)})\) : フォワードLiborベクトル \(x^{(i)}\) から、\(T_E\) 満期のスワップ金利を導出する関数
- \(h_M(x^{(i)}):= h_M(S_M(x^{(i)}))\) : i 番目のフォワード Libor ベクトルのサンプル値から計算される \(T_M\)時のPayoff関数(但しニュメレールとの相対価格)
- \(A_\tau (θ_M)~:~θ_M\) を基準としたオプションの行使領域
- \(\tau_{\theta_M}~:~θ_M\) を基準とした停止時間(\(T_M\) 時における行使境界)
- \(I_{ \{ S_M (x^{(i)})∈ A_\tau(θ_M)\}}\) : 各サンプルから導出されたスワップ金利\(S_M (x^{(i)})\)が行使領域にあれば 1 を返し、そうでなければ 0 となる指示関数
- 次に、\(T_{M-1}~時の~θ_{M-1}\) を求めます。この時も、\(T_{M-2}\) まで、すべてのサンプルについてオプションは行使されなかったと仮定し、一方で \(θ_M\) は既に求まった値を使います。そして適当な Optimizer を使って \(θ_{M-1}\) の最適値を求めます。すなわち、\(θ_{M-1}\) の基準でオプション行使を判断し、\(θ_{M-1}\) ではオプションを行使しなかった場合は、それらのサンプルのみ、\(T_M\) 時において、今度は \(θ_M\) に従った行使判断を行います。行使領域側にあれば、行使価値 を計算し、なければ 0 とします。その上ですべての経路のサンプル平均 \(\hat {V}_{M-1}^{(m_1)}(\bf x)\) が最大になるような \(θ_{M-1}\) を求めます。すなわち、 \[ \begin{align} & \small { \sup_{\theta_{M-1}∈R^+} \hat{V}_{M-1}^{(m_1)} (x) } \\ & \small~~但し~~ {\hat{V}_{M-1}^{(m_1)}(x) } \\ & \small {=\frac {1}{m_1} \sum_{i=1}^{m_1} \left[h_{M-1}(x^{(i)}) I_{\{S(x^{(i)})∈A_τ(\theta_{M-1})\}} +h_M (x^{(i)})I_{\{S_{M-1}(x^{(i)}) ∉ A_τ(\theta_{M-1})\}}I_{\{S_M (x^{(i)})∈A_τ(\theta_M)\}}\right] }\\ & ~~ \tag{6.136} \end{align} \]
- 4.のアルゴリズムを、時間軸を遡及しながら行い、\(θ_{M-2},θ_{M-3},…,θ_1\) を順番に求めます。\(θ_1\) まで求まれば、ベクトル \(\{θ_1,…,θ_M \}\) すなわち行使境界曲線(行使戦略)が決まります。
- さらに、モデルに従ったサンプル経路を \(m_2\) 個生成。これらのサンプルは、\(m_1\) とi.i.d(独立同一分布に従う)なサンプルとして生成されなければなりません。
- 5.で求めたパラメータ \(\{θ_1,…,θ_M \}\) を使った行使戦略に従って、6.のサンプルで MCS を行う。オプション価格は、そのサンプル平均として、下記式で求まります。 \[ \hat{V}_0^{(m_2)}=\frac {1} {m_2} \sum_{j=1}^{m_2} h_τ(θ)(x_τ(θ)^{(j)}),~~~j=1,…,m_2 \tag{6.137} \]
上記のアルゴリズムの中で、ステップ 5.の段階で、 \(m_1\) のサンプル平均としてオプション価値はすでに求まっています。しかし、この段階でのサンプル平均は、本来なら分からないはずの将来の情報を使って求めた行使戦略に基づいた価格になり、価格に上方バイアスがかかっています。同時に、行使戦略 \(\{θ_1,…,θ_M \}\) は、必ずしも最適行使戦略ではないので、これを使ったサンプル平均は下方バイアスがかかります。バイアスが、上方と下方の両方にかかっている場合、サンプル平均と真の期待値の間の位置関係が分らなくなるので、真の平均がどの辺りにあるか求めるのは困難になります。そこで、(必ずしも最適ではない)行使戦略 \(\{θ_1,…,θ_M \}\) を使って、新たに生成された \(m_2\) サンプルを使う事により、バイアスは下方のみになります。
このようにして生成された、行使戦略(すなわち停止時間) \(τ(θ)\) は、極めて恣意的な行使境界曲線の関数形であり、当然最適行使戦略からずれています。しかし、そのずれが少々大きくても、計算されるオプション価値はあまり大きく動かない事が、経験的に知られています。また、Random Tree Method と比べると、必要とするサンプル数が、行使境界曲線を推定する用 \(m_1\) と、実際にそれを使ってサンプル平均を導出する用 \(m_2\) だけで済むので、はるかに少ない数で MCS が行えます。90 年代の前半ころまでは、この方法でのアメリカンタイプのオプション価格導出が主流だったようです。但し、明確に上方バイアスがかかった価格の導出アルゴリズムが無く、信頼区間の範囲に真の期待値が含まれているかどうか、確認できない点は注意が必要です。