上級編 6. Libor Market Model
6.6 モンテカルロシミュレーション
6.6.6 アメリカンタイプのオプションへの対応(続き)
6.6.6.5 Least Squares Mote-Carlo("LSM" 最小2乗モンテカルロ法)
6.6.6.5.1 LSM のアルゴリズムの概要
繰り返しになりますが、アメリカンタイプのオプションの価格計算の基本となる考え方は、オプション行使日にその時の対象資産の価格(確率変数の値)をもとに、そこでオプションの行使価値と、継続保有価値を比較し、その高い方がオプション価値になるというものでした。それを数式で示した 6.126 式を再記します。
\[ V_i(x_i)=\max(h_i(x_i),c_i(x_i))=\max\left(h_i (x_i ),E\left[V_{i+1}(x_{i+1})~|~x_i \right]\right) \tag{6.126} \]右辺の max 関数中にある条件付き期待値 \(E\left[V_{i+1}(x_{i+1})~|~x_i\right]\) を、Random Tree Method では、各 \(x_i\) からさらにサンプル経路を多数発生させシミュレーションして求めようとするものでした。また Stochastic Mesh Method では、i.i.d.に生成された他のサンプルのオプション価値から、尤度比を使った加重サンプル平均でそれを求めようとするものでした。
Longstaff- Schwartz らは、この継続保有価値c_i (x_i )の関数形を、大胆にも、適当な基底関数の線形結合で近似できると看做しました(Longstaff-Schwarz "Valuing American Option by Simulation")。そして、その基底関数の係数パラメータを、サンプル経路上の最終行使日における行使価値を基に、回帰分析で求めるスキームを提示しました。そのアルゴリズムを簡単に示すと下記のようなものになります。
- まず、モデルに従った確率変数のサンプル経路を、オプションの最終行使日(スワップションの場合は、対象スワップの最終期日)まで生成します。各サンプルは、それぞれ独立でモデルに従った分布に従う(i.i.d.)なサンプルとなります。
- 1.で生成されたサンプル経路上の最終行使日のオプション価値は、行使価値に一致します。その情報を使って、最終行使日の一期手前の行使日における継続保有価値を下記のように、基底関数の線形結合で近似できると看做します。
\[ \begin{align}
E(V_M(x_M)~|~x_{M-1})
& =E \left[\max(h_M(x_M~|~x_{M-1}),0)\right] =E \left[h_M(x_M )~|~x_{M-1} \right] \\
& =c_{M-1}(x_{M-1}) \\
& ≈ c_{M-1}^* (x_{M-1}) = \sum_{k=1}^N β_{M-1,k} ψ_{M-1,k}(x_{M-1}) \tag{6.148}
\end{align}
\]
但し、\(ψ_{ik}(x_i)~と~β_{ik},~~k=1,…,N\) は、それぞれ、行使日 \(T_i\) ごとに、適当に決めた N 個の基底関数とその係数ベクトルになります。基底関数は、商品ごとに Payoff 関数を分析して heuristic に決めたものを外生的に与えます。具体的な関数形の例は、後程述べます。そして、最右辺にある基底関数の係数パラメータ \(β_{M-1,k}\) を、最終行使日におけるサンプル経路上のオプション価値データから、回帰分析で求めます。以下、式中で \(c_i(x_i)\) は理論値を示し、\(c_i^*(x_i)\) 回帰分析で得られた基底関数による関数形を示すものとします。
- これで、\(T_{M-1}\) 時における継続保有価値 \(c_{M-1}^*(x_{M-1})\) を示す関数形が求まったので、\(T_{M-1}\) 時の各ノードにおけるオプション価値は下記式で求まります。
\[ \begin{align}
V_{M-1}(x_{M-1}^{(j)}) & ≈ \hat{V}_{M-1}(x_{M-1}^{(j)}) \\
& = \max\left[h_{M-1}(x_{M-1}^{(j)}),~ c_{M-1}^* (x_{M-1}^{(j)}) \right],~~~~j=1,…,m \tag{6.149}
\end{align}
\]
- さらに、このようにして \(T_{i+1}\) 時のオプション価値が求まったとして、そこから \(T_i\) 時の継続保有価値 \(c_i^*(x_i)\) の関数形を回帰分析で求めます。
\[
c_i^*(x_i) = E \left[ \hat{V}_{i+1}(x_{i+1})~|~x_i \right] =\sum_{k=1}^N β_{ik}ψ_{ik}(x_i) \tag{6.150}
\]
ここから、\(T_i\) 時のオプション価値は、
\[
V_i(x_i^{(j)}) ≈ \hat{V}_i(x_i^{(j)})
= \max\left[h_i(x_i^{(j)}),c_i^*(x_i^{(j)})\right],~~~j=1,…,m \tag{6.151}
\]
となります。
- このアルゴリズムを、時間軸を遡及しながら \(T_1\) 時まで遡り、そのサンプル平均を求めれば、それがオプション価格になります。 \[ V_0 = E\left[ V_1(x_1)\right] ≈ E \left[\hat{V}_1(x_1)\right] = \frac 1 m \sum_{j=1}^m \max\left[h_1^{(j)}(x_1^{(j)}),~c_1^*(x_1^{(j)})\right] \tag{6.152} \] (\(V_i(x_i)\) はニュメレールとの相対価格としているので、そのニュメレール測度下での期待値は現在価格に一致します。)
このアイデアを、直観でも理解できるよう、グラフを使って解説します。
まず 1.のステップですが、確率変数のサンプル経路を、オプションの最終行使日 \(T_M\) まで m 個シミュレーションしたとします。\(T_M\) 時では、継続行使価値は 0 なので、オプション価値は行使価値に一致します。すなわち、 \[ \hat{V}_M(x_M^{(j)}) = \max\left[h_M (x_M^{(j)}),~c(x_M^{(j)})=0\right] = h_M (x_M^{(j)}),~~~j=1,…,m \] これで、各サンプル経路上の、最終行使日におけるオプション価値が求まりました。
次に、一期前の行使日におけるオプション価値は、 \[ \hat{V}_{M-1}(x_{M-1}^{(j)}) =\max\left[h_{M-1}(x_{M-1}^{(j)}),~c_{M-1}(x_{M-1}^{(j)})\right] \] となります。ところで、\(c_{M-1}(x_{M-1}^{(j)})\) ですが、各サンプル経路上の \(\hat{V}_M(x_M^{(j)}~|~x_{M-1}^{(j)})\) の値は1.で、すでに求まっています。それをグラフに散布図としてプロットすると、下記のようになります。但し、横軸は、\(T_{M-1}~時のサンプル値~x_{M-1}^{(j)}\) で、それに対応する \(\hat{V}_M(x_M^{(j)}~|~x_{M-1}^{(j)})\) がプロットされています(従って、満期 Payoff 関数の曲線とは一致しません)。さらにそれを、サンプル生成の順番 \(j=1,…,m\) ではなく、値の 低い方から順番にならべ変えています。
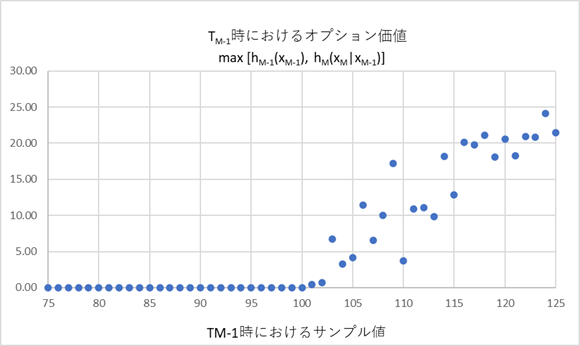
グラフを見れば分かる通り、サンプル経路上のオプション価値 \(\hat{V}_M \left(x_M^{(i)}~|~ x_{M-1}^{(i)}\right)\) はその期待値 \(E \left[V_M (x_M^{(i)})~|~x_{M-1}^{(i)}\right]\) とは一致せず、それより大きかったり小さかったりします。
ここで、上の散布図上の各点の近似曲線を描いてみます。
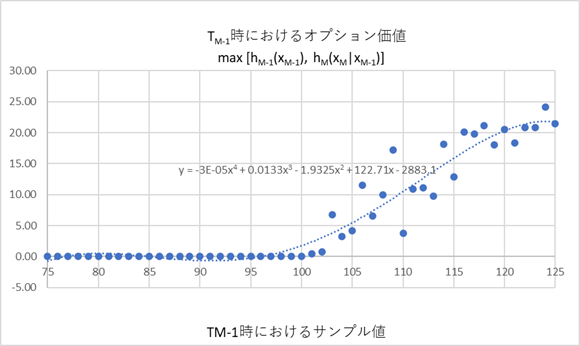
この曲線(グラフ上の点線部分)が、上記の 2.のステップで求めようとした、6.148 式の、\(c_{M-1}^*(x_{M-1})=\sum_{k=1}^N β_{M-1,k} ψ_{M-1,k}(x_{M-1})\) に相当します。 上のグラフでは、Excel に備わった回帰曲線の描画機能を使っています。ここでは基底関数として x の4次の多項式を与えて、Excel が最小2乗法を使って基底関数の各係数を導出しています。なので \(ψ_{M-1,k}~はそれぞれ~x^4,~x^3,~x^2,~x,~1\) となり、それぞれの係数 \(β_{M-1,k}\) は、グラフ中にある関数 y に示されています。グラフでは、サンプル値が高いエリアで、下に凹(cocave) になり、不自然な形になっていますが、実践では、基底関数の組み合わせを工夫して、より継続保有価値曲線に近そうな関数形を heuristic に選びます。
これで \(T_{M-1}\) 時における継続保有価値が近似されたので、\(T_{M-1}\) 時のオプション価値は、6.149 式 の通り、各サンプルに対応した継続保有価値と、行使価値を比較し、その高い方になります。これが上記のステップ3.です。
\(T_{M-1}\) 時の各ノードのオプション価値 \(\hat{V}_{M-1}(x_{M-1}^{(j)}),~j=1,…,m\) が求まったので、\(T_{M-2}\) 時からみた、継続保有価値が、やはり近似曲線で求まります。さらに継続保有価値と行使価値を比較すれば、\(T_{M-2}\) 時のオプション価値が求まります。同様に \(\hat{V}_{i+1}(x_i)\) が求まれば、\(T_i\) 時からみた継続保有価値 \(c_i^*(V_{i+1}(x_{i+1})~|~x_i)\) が求まり、さらに、それと行使価値を比較すればオプション価値 \(\hat{V}_i(x_i)\) も求まります。これが、ステップ 4.のアルゴリズムです。これをグラフで見てみます。下のグラフは、サンプル \(x_i^{(j)},~~j=1,…,m~ に対応する~\hat{V}_{i+1}(x_{i+1}^{(j)}~|~x_i^{(j)})\) の値をグラフにプロットし、さらに、各点を近似する回帰曲線を示しています。
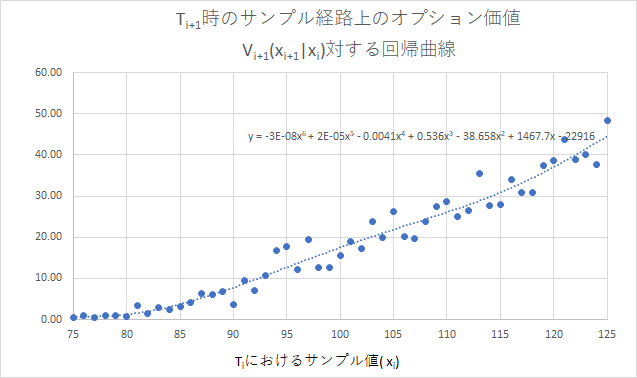
ここでも、Excel の近似曲線を描く機能を使い、x の 6次式で近似していますが、これが 6.150 式(下に再記します)に相当します。
\[ c_i^*(x_i) = E \left[ \hat{V}_{i+1}(x_{i+1})~|~x_i \right] =\sum_{k=1}^N β_{ik}ψ_{ik}(x_i) \tag{6.150} \]x の 6次式なので、\(ψ_{i,k}(x_i),~k=1,…,7~を~ x^6,~x^5,…,~x,~1\) として外生的に与えると、その係数 \(β_{i,k}\) は、Excelが最小2乗法を使って自動的に計算します。計算結果は、グラフ上の回帰曲線の関数形y(x)の通りです。さらにここから \(T_i\) 時におけるオプション価値は 6.151 式で求まります。(実践では、自分で基底関数を決め、自分で係数の導出アルゴリズムをプログラム化します。)
このアルゴリズムを、\(T_1\) まで遡及すれば、最終的に現時点のオプション価値が求まります。これが最後の 5.のステップです。
以上のアルゴリズムで、重要なポイント2点について、次のセクションで説明します。1点目は、基底関数としてどのようなものを選択すべきかです。2点目は、上記のアルゴリズムでは、価格に上方バイアスがかかるので、信頼区間の間に真の価格が入るようにする為には、別途下方バイアスがかかった価格も導出する必要があるという点です。
6.6.6.5.2 基底関数
基底関数 \(ψ_{i,j}(x_i)\) については、Longstaff-Schwartz の論文、あるいは Glasserman本でいくつか例示されています。Glasserman本では、x の累乗や、x がベクトルの場合((\(x=\{x_1,x_2,…,x_d\}\))は、各 x の累乗に加え、各変数同士の積 \(x_i^p x_j^q,~~p,q=0,1,…,n\) などが例示されています。Longstaff-Schwartz の論文では、ラゲールの多項式や、エルミート、ルジャンドル、チェビチェフの多項式なども使えるとされています。また基底関数には定数項も含める必要があります。さらに、Payoff 関数や、確率変数のモーメント、ヨーロピアンオプションの価格式なども、基底関数になり得るとされています。これらは、Control Variates Method の所で説明した通り、制御変量の役割を果たしています。
基底関数の数は、多いほど回帰曲線の説明力が上がりますが、多すぎると Over-Fitting の問題や、回帰分析に時間がかかりすぎるという問題も出てきます。Longstaff-Schwartz の論文では、基底関数の数は、各確率変数に対し、定数項も含めせいぜい 4 個程度で問題無いと述べられています。マルチファクターモデルでは、基底関数の数はファクター数に応じて増加しますが、指数的に増やす必要はなく、ファクター数× 3~4 で十分誤差の小さいシミュレーションが出来るようです。すでに、パラメトリックな行使境界曲線の方法の所で説明した通り、オプションの行使戦略を決める行使境界曲線は、かなり適当な近似であっても、シミュレーションされた価格に大きな差が出ない事が経験的に知られています。継続保有価値を基底関数で近似する場合でも、結局それは行使境界曲線を推察するのと同じ事なので、若干の誤差は、シミュレーション結果に大きな影響を及ぼさないということです。
Heuristic に基底関数を決めていくには、商品性の分析や、上記のようにグラフにして形状の違和感を消していくことになります。アナログ的ですが、MCS の様々なテクニックは往々にしてこのようなものです。例えば上のグラフでは、グラフの右の方、すなわちより Deep in the Money の領域で、曲線が Concave(凹曲線)になっている点と、Deep Out of the Money の領域で、マイナスの値を取っている点に違和感があります。前者の問題については、heuristicに基底関数の組み合わせをいろいろ試して、最もそれらしい形のものを選べばいいでしょう。一方、後者の問題は、オプション価格がマイナスになる領域が発生するので、若干問題です。Longstaff-Schwartz は、近似曲線を In the Money の領域だけで描く方法を提案しており、そうすれば後者の問題は解決します。
6.6.6.5.3 回帰分析による基底関数の係数ベクトルの導出方法
上記の回帰曲線を示したグラフは、Excel のグラフ機能を使って描いています。実際に自分でプログラムに落とし込む際は、線形代数のテクニックを使います。Glasserman 本から、その方法を簡単に説明します。
継続保有価値を基底関数の線形結合で近似する式は、下記のようなものでした(6.150式を少し表記を変えています)。
\[ E \left[ V_{i+1}(x_{i+1})~|~x_i \right]=c_i(x_i) \approx c_i^*(x_i) =\sum_{k=1}^N β_{i,k} \cdot ψ_{i,k}(x_i)=\bf β_i \cdot ψ_i (x_i ) \]最右辺は、N 次元の基底関数のベクトルと、その係数ベクトルの内積として表記しています。ここから、
\[ E\left[V_{i+1}(x_{i+1})~|~x_i \right] \approx {\bf β_i \cdot ψ_i (x_i) } \tag{6.153} \]という関係式が導出できますが、これを \(β_i\) について解くと、
\[ {\bf β_i}= \left[ E({\bf ψ_i(x_i) \cdot ψ_i(x_i)^⊤ }) \right]^{-1} E \left( {\bf ψ_i(x_i)} V_{i+1}(x_{i+1})\right) \tag{6.154} \]なぜこうなるか、残念ながらその導出過程を説明する能力は持ち合わせていませんが、6.154 式の両辺にベクトル \(\bf ψ_i(x_i)\) を作用させれば、\(E \left[V_{i+1}(x_{i+1})~|~x_i\right] ≈ \bf β_i \cdot ψ_i(x_i)\) となる事から、自分なりに、なんとなく理解しています。
ここで、右辺は、ベクトル \(E \left( {\bf ψ_i(x_i)} V_{i+1}(x_{i+1})\right)\) に、行列 \(\left[ E({\bf ψ_i(x_i) \cdot ψ_i(x_i)^⊤ }) \right]\) の逆行列を作用させている形になっている点に気が付いて下さい。このベクトルと行列をそれぞれ、下記のように表記し、6.145式を書き換えます。
\[ \begin{align} & E \left( {\bf ψ_i(x_i)} V_{i+1}(x_{i+1})\right) :={\bf b_{ψ V} }, \\ & \left[ E({\bf ψ_i(x_i) \cdot ψ_i(x_i)^⊤ }) \right] :=[{\bf B_{ψ_i}}] \\ & {\bf β_i}= \left[ E({\bf ψ_i(x_i) \cdot ψ_i(x_i)^⊤ }) \right]^{-1} E \left( {\bf ψ_i(x_i)} V_{i+1}(x_{i+1})\right) = [{\bf B_{ψ_i}}]^{-1} \cdot {\bf b_{ψ V} } \tag{6.154'} \end{align} \]但し、\(\bf [B_{ψ_i}]^{-1}~は~N×N\) 次の行列で、その各要素はベクトル \({\bf ψ_i(x_i)}=\{ψ_{i,1},…,ψ_{i,N}\}\) の各要素同士の積 (\(ψ_{i,k}\times ψ_{i,l},~~k,l =1,…,N\))の期待値になります。また \(\bf b_{ψV}\) は N 次のベクトルで、基底関数ベクトル \(\bf ψ_i(x_i)\) にスカラ値 \(V_{i+1}(x_{i+1})\) をかけたものの期待値になります。
また、最小二乗法を使った回帰分析では、回帰直線(曲線)の係数(ベクトル)は、説明変数を x と被説明変数を y とすると、" xy の共分散 / x の分散" となる事が知られていますが、\(\bf \left[B_{ψ_i}\right]^{-1}\) は \(\bf ψ_i\) の分散の逆行列なので、分散での割り算を意味し、\(\bf b_{ψV}\) は \(\bf ψ_i\) と \(V_{i+1}(x_{i+1})\) の共分散を示すと理解すれば、上の式の意味が理解しやすくなると思います。 ここでは、基底関数 \(ψ_i\) が説明変数で、オプション価値 \(V_{i+1}(x_{i+1})\) が被説明変数です。
さて、上の式では、行列 \(\bf \left[B_{ψ_i}\right]\) もベクトル \(\bf b_{ψV}\) も期待値を示しています。これを、サンプルを使って、サンプル平均で求めます。まず、行列\(\bf \left[B_{ψ_i}\right]\) ですが、各要素は基底関数同士の積になっており、基底関数は外生的に与えられています。したがって、基底関数にサンプル値を与えて、その積のサンプル平均を計算すれば求まります。すなわち
\[ E\left( ψ_{i,k}(x_i) \cdot ψ_{i,l}(x_i)\right) ≈ \frac 1 m \sum_{j=1}^m ψ_{i,k} (x_i^{(j)})~ψ_{i,l}(x_i^{(j)}),~~~ k,l =1,…,N \tag{6.155} \]また、ベクトル \( \bf b_{ψV}\) ですが、これも同様に、ベクトルの要素ごとにサンプル平均を求めます。
\[ E \left[ ψ_{i,k}~ V_{i+1}(x_{i+1})\right] ≈ \frac 1 m \sum_{j=1}^m ψ_{i,k}(x_i^{(j)}) V_{i+1}(x_{i+1}^{(j)}),~~~ k,=1,…,N \tag{6.156} \]このようにしてサンプル平均で求めた行列 \(\bf \left[B_{ψ_i}\right]\) の逆行列を求めれば、係数ベクトル \(\bf β_i\) は \(\bf \left[B_{ψ_i}\right]^{-1}\cdot b_{ψV}\) で求まります。逆行列の計算は、若干時間がかかります。また行列式が 0 だと計算できないので、行列が正則行列でなければなりません。サンプル値で、行列の要素を求めれば、大抵の場合、正則行列になるので問題ないでしょう。
6.6.6.5.4 バイアス
上記のアルゴリズムでも、Random Tree Method や Stochastic Mesh Method と同様、導出されたオプション価格には、上方バイアスがかかっています。理由も、他の方法と同じで、数学的にはジェンセンの不等式によるもので、直感的には、本来知ることのできない将来の情報を使って継続保有価値を計算しているからです。そこで、この方法でも下方バイアスのかかった価格を別途導出し、信頼区間をオーバーラップさせて真の価格が一定確率でその範囲内に収まるという推定ができるようにします。
Longstaff-Schwartz は、下方バイアスのかかった価格が導出できるアルゴリズムとして、以下のような方法を提案しています。すなわち、オプション価値を求める式 \[\hat{V}_i (x_i^{(j)}) = \max\left[h_i(x_i^{(j)}),c_i^* (x_i^{(j)})\right] \] を、次のように変えます。
\[ \begin{eqnarray} \hat{V}_i(x_i^{(j)})= \begin{cases} if~~h_i(x_i^{(j)}) ≥ c_i^*(x_i(j))~~~~then~~ h_i(x_i^{(j)}) \\ if~~h_i(x_i^{(j)}) \lt c_i^*(x_i^{(j)})~~~~ then ~~ \hat{V}_{i+1}(x_{i+1}^{(j)}) \end{cases} \tag{6.157} \end{eqnarray} \]この方法の意味するところは、もし行使価値が回帰分析で求めた継続保有価値を上回る場合は、行使価値=オプション価値とし、逆に行使価値が回帰分析で求めた継続保有価値を下回る場合は、回帰分析で求めた \(c_i^*(x_i^{(j)})\) をオプション価値として使うのではなく、すでに、時間軸を遡及しながら求めた、サンプル経路上のオプション価値を継続保有価値として使うものです。仮に、継続保有価値として \(c_i^*(x_i^{(j)})\) を使った場合、この値は、本来知ることができない将来の情報を使って計算したもので、上方バイアスがかかります。しかし、Longstaff-Schwartz の方法では、\(c_i^*(x_i^{(j)})\) は、オプションの行使戦略の判断にのみ使うだけで、実際のオプション価値はサンプル経路上のそれを使います。サンプル経路上の情報であれば、サンプル数を増やせば、大数の法則により、バイアスがかからずに真の値に近づいていきます。(数学的な証明や解説は省略します。)
下方バイアスがかかった価格の導出方法は、Random Tree Method や Stochastic Mesh Method と同じように、行使戦略に使ったデータと、実際にオプション価値を計算するのに使うデータを分けるのでした。Longstaff-Schwartz の上記の方法は、基底関数による継続保有価値は、行使戦略の判断にのみ使われ(すなわち、\(c_i^*(x_i^{(j)}\) がオプション価値として使われる事は無いという事です)、オプション価値の計算に使うサンプルは、最初に生成したサンプルをそのまま使います。サンプルを別途生成する必要が無いので、その分高速になります。
6.6.6.5.5 Stochastic Mesh Methodへの応用
Glasserman本では、この最小2乗モンテカルロ法を、Stochastic Mesh Method にも応用できるとしています。Stochastic Mesh Method を使うには、遷移確率密度関数が求まっている事が必要条件ですが、もしそれが解析的に求まっていなくても、数値的に求まれば、その方法を使う事ができます。下記の、最小2乗モンテカルロ法による、継続保有価値を基底関数の線形結合で近似し、基底関数の係数ベクトルを求める式を見てください。6.154式を使って、\(\bf \beta_i~を~ \left[{\bf B_{ψ_i}}\right]^{-1} \cdot {\bf b_{ψ V}}\) に置き換えています。
\[ \begin{align} c_i^* (x_i^{(j)}) & = \sum_{l=1}^N β_{i,l}~ψ_{i,l}(x_i^{(j)}) \\ & ={\bf ψ_i}(x_i^{(j)})^{\top} \cdot {\bf β_i} = {\bf ψ_i}(x_i^{(j)})^{\top} \cdot {\bf \left[B_{ψ_i}\right]^{-1} \cdot b_{ψV}} \\ & =\frac 1 m \sum_{k=1}^m \left({\bf ψ_i}(x_i^{(j)})^{\top} {\bf \left[B_(ψ_i)\right]~ψ_i}(x_i^{(k)})\right) \hat{V}_{i+1}(x_{i+1}^{(k)}) \end{align} \]上記式の \(\left({\bf ψ_i}(x_i^{(j)})^{\top} {\bf \left[B_(ψ_i)\right]~ψ_i}(x_i^{(k)})\right)\)を j ノードから k ノードへのウェイトと看做せば、上式は、次のように書き換えられます。
\[ \begin{align} c_i^* (x_i^{(j)}) & =\frac 1 m \sum_{k=1}^m \left({\bf ψ_i}(x_i^{(j)})^{\top} {\bf \left[B_(ψ_i)\right]~ψ_i}(x_i^{(k)})\right) \hat{V}_{i+1}(x_{i+1}^{(k)}) \\ & =\frac 1 m \sum_{k=1}^m W_i^{jk} \hat{V}_{i+1}(x_{i+1}^{(k)}) \tag{6.158} \end{align} \]これは、Stochastic Mesh Methodで継続保有価値を独立なサンプル上のオプション価値の加重平均で近似した式と同じ形になります。したがって、最小2乗モンテカルロ法は、基底関数をつかった回帰分析により、Stochastic Mesh Methodにおける尤度比を数値的に求めているとも言えます。すると、Stochastic Mesh Method は、繊維確率密度関数が解析的に求まっていなくても、使う事ができます。
< 最後に >
最小2乗モンテカルロ法は、これまで説明した様々な方法の中でも、最も広範な商品に適用可能なアルゴリズムで、かつ計算時間も他の方法よりもかかりません。その為、2000年代以降は、この方法が主流になっていると推察します。(各証券会社の価格エンジンのアルゴリズムの中身までは判りません) Libor Market ModelをMCSでシミュレーションする場合、バーミューダンタイプのオプションの価格計算では、この方法を使うのがいいでしょう。ただし、その場合、確率変数に対して回帰分析を行うのではなく、確率変数となるフォワードLiborベクトルから、ゼロクーポン債価格や、フォワードスワップ金利を導出し、それに対して回帰分析を行う形になります。いずれにしても、それらのテクニックは、商品ごとに具体的にアルゴリズムを考える必要があります。ここでは、MCSの一般論にとどめ、後で個別のエキゾチック商品を紹介する機会があれば、そこで説明できればと思います。