上級編 1. イールドカーブ
1.1 Interpolation
1.1.6 Forward Monotone Convex Spline法
1.1.6.1 イントロダクション
これまでのInterpolation法で出てきた問題は、かなりの部分、瞬間フォワードカーブの形状の問題に帰結します。Linear Interpolationでは、瞬間フォワードカーブが非連続になったり、無理に連続にしようとすると、激しい波形が発生したりします。Cubic Spline法では、Bessel(Hermite) Cubic Spline法を使うと、瞬間フォワードカーブは連続にはなるものの、微分不可能で、やはり大きな波が発生したりします。また、2階微分可能なCubic Spline法を使えば、瞬間フォワードカーブも微分可能になり、より滑らかになりますが、局所性が失われ、あるPillarにおけるPar Curveの摂動が、Zero Curve全体に波及していき、瞬間フォワードカーブはそれが増幅されて波が発生するような影響を与えます。さらに、いずれの方法も、Zero Rate Curveが常に正の値を取ったとしても、そこから導出される瞬間フォワードカーブが一部の領域でマイナスになる可能性があります。マイナス金利が日本や欧州で常態化している現在、インターポレーションした結果マイナス金利が発生する事自体は、致命的な問題で無くなりました。しかし、それが、Pillar間の不自然におおきな“たわみ”から発生しているのであれば、その“たわみ”自体が問題であると言えます。
Hagan-Westは、2006年の論文の中で、瞬間フォワードカーブが、Par CurveやZero Rate Curveの幾何学的な性質(単調増加性や単調減少性)を維持したまま、不自然な“たわみ”によるマイナス金利の発生を抑制するようなInterpolationの方法を紹介しています。
この方法は、これまでのInterpolation法が、各PillarにおけるZero RateあるいはZero Rateに期間をかけた値を補間していたのに対し、各Pillarにおける"瞬間"フォワード金利を補間する方法です。ところが、区間フォワード金利は、原データとなるPar Curveから一意に決まりますが、各Pillarにおける"瞬間"フォワード金利は一意に決まりません。そこで、一定のルールを決めて、Pillarにおける瞬間フォワード金利をあらかじめ決めておき、Pillar間の瞬間フォワード金利の平均が区間フォワード金利と一致するようなカーブを描きます。以下にその手順を示します。
1.1.6.2 基本となるInterpolatorの関数形
< 各Pillarにおける瞬間フォワード金利 >
Pillar の配列を \(t_i,\ i=0,1,…,n\) とします。但し \(t_0\) は現時点とします。また、各Pillar におけるZero Rate はPar Curve からBootstrapping を使って導出済で既知とします (但し、Bootstrapping + Interpolationのアルゴリズムの中では、最初は推定値を設定する)。そうすると、Pillar間 \([t_{i-1},t_i]\) の区間フォワード金利: \(f_i^d\) は \(t_{i-1}\) と \(t_i\) の Zero Rate から一意に決まります。
一方、各Pillarにおける瞬間フォワード金利:f_i は、一意に決まりません。そもそも、補間しようとしているPillarのデータが一意に決まらなければ、補間のしようがありません。そこで、Hagan-Westは、まず各Pillarにおける瞬間フォワード金利を、前後の区間の区間フォワード金利の期間加重平均になると仮定します。すなわち
\[ f_i=\frac{t_i-t_{i-1}}{t_{i+1}-t_{i-1}} f_{i+1}^d+\frac{t_{i+1}-t_i}{t_{i+1}-t_{i-1}} f_i^d,\ \ for\ i=1,2,…,n-1\ \tag{1.1.38} \]これで、両端の Pillar \(t_0,\ t_n\) を除いて、各 Pillar における瞬間フォワード金利の値が定義できました。さらに、両端の瞬間フォワード金利については、上の式から求まる \(f_1\) と、\(f_{n-1}\) を使って、それぞれ \(f_0_) と \(f_n_) と直線で結び、その平均(直線を積分した値)が区分フォワード金利と一致するような\(f_0_) と \(f_n_)に設定します。式で表現すると、次の様になります。
\[ f_0=f_1^d-\frac{1}{2}(f_1-f_1^d),\ \tag{1.1.39} \] \[ f_n=f_n^d-\frac{1}{2} (f_{n-1}-f_n^d),\ \tag{1.1.40} \]これで、すべてのPillarにおける瞬間フォワード金利が決まりました。続いて、これをInterpolationします。
< 基本となるInterpolatorの関数形 >
求めるInterpolatorを、各Pillarの瞬間フォワード金利を通る2次のSpline関数と想定します。
\[ f(t)=K+L x(t)+M x(t)^2,\ \ \ x(t)=\frac{t-t_{i-1}}{t_i-t_{i-1}},\ \ t\in [t_{i-1},t_i] \]この2次関数の係数 K,L,M を、下記の条件を設定することで求めます。
- \(f(t)\) は各Pillarにおいて、1.1.38 式で定義した瞬間フォワード金利の値と一致し
- かつPillar間の瞬間フォワード金利の平均は、その区間の区間フォワード金利と一致する(この条件は、Arbitrage Freeの為の絶対条件です。) 式で表すと、 \[ f(t_{i-1})=f_{i-1},\ \ f(t_i)=f_i,\ \ \ \ \ \frac{1}{t_i-t_{i-1}} \int_{t_{i-1}}^{t_i} f(t)dt=f_i^d, \]
方程式を解くと係数 K,L,M が求まり、Interpolatorは、区間フォワード金利と、各Pillarにおける瞬間フォワード金利を使って、下記のように表記できます。
\[ f(x(t))=f_{i-1}-(4f_{i-1}+2f_i-6f_i^d)x(t)+(3f_{i-1}+3f_i-6f_i^d)x(t)^2 \\ =(1-4x(t)+3x(t)^2)f_{i-1}+(-2x(t)+3x(t)^2) f_i+(6x(t)-6x(t)^2) f_i^d,\ \tag{1.1.41} \]但し、\(x(t)=\frac{t-t_{i-1}}{t_i-t_{i-1}},\ \ \ t\in [t_{i-1},t_i]\)
この式の右辺は、\([t_{i-1},t_i]\) の区間と、その両側の区間 \([t_{i-2},t_{i-1}],\ [t_i,t_{i+1}]\) に対応する区間フォワード金利 \(f_{i-1}^d,\ f_i^d,\ f_{i+1}^d\) だけを使っても表記できます。(_(x(t)=x_) と置き換えます)
\[ f(x)=f_i^d-\frac{t_i-t_{i-1}}{t_i-t_{i-2}}(f_i^d-f_{i-1}^d)(1-4x+3x^2)+\frac{t_i-t_{i-1}}{t_{i+1}-t_{i-1}} (f_{i+1}^d-f_i^d)(-2x+3x^2),\ \tag{1.1.42} \]すなわち、\(f(x)\) は \(f_{i-1}^d,\ f_i^d,\ f_{i+1}^d\) にしか依存しておらず、局所的です。
そして、この式を \(f_{i-1}^d,\ f_i^d,\ f_{i+1}^d\) の関数とみなし、それぞれで偏微分すると、次の様な不等式が導けます。 (\(x\in [0,1]\) の範囲で、各偏微分係数の値の最大値と最小値を求めて導出)
\[ -\frac{1}{3} \frac{t_i-t_{i-1}}{t_i-t_{i-2}} \lt \frac{\partial f}{∂f_{i-1}^d} \lt \frac{t_i-t_{i-1}}{t_i-t_{i-2}},\ \tag{1.1.43} \] \[ 0 \lt \frac{\partial f}{\partial f_i^d} \lt \frac{3}{2},\ \tag{1.1.44} \] \[ -\frac{1}{3} \frac{t_i-t_{i-1}}{t_{i+1}-t_{i-1}} \lt \frac{\partial f}{\partial f_{i+1}^d} \lt \frac{t_i-t_{i-1}}{t_{i+1}-t_{i-1}},\ \tag{1.1.45} \]すなわち、各偏微分が有界であり、区間フォワード金利の変化(それの元になっているPar RateやZero Rate)の変化に対し、瞬間フォワード金利の変化が安定している事を意味します。
1.1.6.3 単調性(Monotonicity)の調整
上記で定義したInterpolatorについて、次の様な単調性の制約を課したいと考えます。すなわち、
- 連続する3区間の区間フォワード金利が、\(f_{i-1}^d \lt f_i^d \lt f_{i+1}^d\) の場合、区間 \(t\in [t_{i-1},t_i]\) にある瞬間フォワード金利 \(f(t)\) は、その区間内で単調増加にしたい。
- 連続する3区間の区間フォワード金利が、\(f_{i-1}^d \gt f_i^d \gt f_{i+1}^d\) の場合、区間 \(t\in [t_{i-1},t_i]\) にある瞬間フォワード金利 \(f(t)\) は、その区間内で単調減少にしたい。
これは、これまでのInterpolation法がすべて、瞬間フォワードカーブが、非連続であったり、連続であっても激しく波打ったりしていたのを、無理やり修正しようとするものです。この意図を、グラフで視覚的に見てみたいと思います。
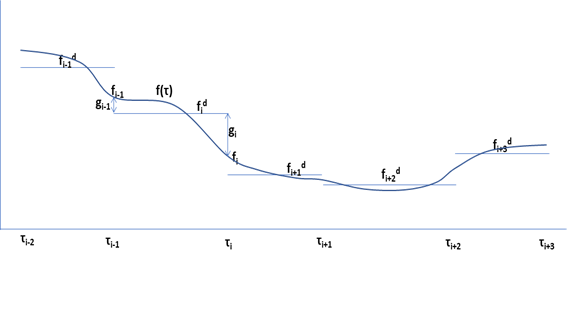
階段関数のような横の直線のグラフは、各Pillar間の区間フォワード金利 \(f_i^d\) を示しています。また、緩やかな曲線が、瞬間フォワード金利をInterpolation したカーブを示しています。1.1.38 式で、各Pillar における瞬間フォワード金利を前後の区間フォワード金利の時間加重平均と定義しているので、各 \(f_i\) は、必ず両隣の\(f_i^d\) と \(f_{i+1}^d\) の間に位置している事が分ります。
そして、単調性の制約は、上のグラフで言えば、\(f_{i-1}^d \gt f_i^d \gt f_{i+1}^d \gt f_{i+2}^d\) なので、その区間では \(f(t)\) は単調減少になって欲しいというものです。また \(f_{i+1}^d \gt f_{i+2}^d \lt f_{i+3}^d\) なので、\(t_{i+1} \lt t \lt t_{i+2}\) の区間では、\(f(t)\) に局所的な最小値が発生するのは許容されます。
ところが、上記の制約条件で機械的に2次Spline関数の係数を決めていくと、区間フォワード金利が単調増加・単調減少している区間において、瞬間フォワード金利のカーブに局所的な最大値あるいは最小値が発生する可能性があります。まずどのような場合にそうなるか、見てみます。
< 区間フォワード金利が単調増加・減少なのにf(t)に局所的な最大値・最小値が発生するケース >
まず、区間 \(t\in [t_{i-1},t_i]\) 内で、瞬間フォワード金利と区間フォワード金利の差を、関数 \(g()\) で表します。
\[ g(t)=f(t)-f_i^d,\ \ t\in [t_{i-1},t_i ] \tag{1.1.46} \]また、この区間の両端における \(g()\) の値を、\(g(t_{i-1}):= g_{i-1},\ g{t_i}:=g_i\) とおきます。次に、瞬間フォワード金利のInterpolator の式(1.1.41)を、\(g(t)=f(t)-f_i^d\) に代入し、\(f_{i-1},\ f_i,\ f_i^d\) を \(g_{i-1},\ g_i\) で置き換えると、\(g(t)\) も \(x(t)=\frac{t-t_{i-1}}{t_i-t_{i-1}}\) の2次関数として表現できます。すなわち
\[ g(t)=g(x(t))=g_{i-1}(1-4x+3x^2)+g_i(-2x+3x^2),\ \ x\in [0,1],\ \tag{1.1.47} \]また、\(g(x)\) の \(x\in [0,1]\) 間の平均(積分)は0になります。
\[ \int_0^1 g(x)dx=0 \]\(g(x)\) は2次関数なので、区間 \(x\in [0,1]\) 内で最大値または最小値を持つ可能性があります。どういう場合にそうなるか、場合分けして考えます。
まず、\(g(x)\) を \(x\) で微分し、\(x\) の区間の両端、すなわち \(x=0, x=1\) における微分係数を導出します。
\[ g'(x)=g_{i-1} (-4+6x)+g_i (-2+6x)\ \tag{1.1.48}\] \[ g'(0)=-4g_{i-1}-2g_i\ \tag{1.1.49}\] \[ g'(1)=2g_{i-1}+4g_i\ \tag{1.1.50}\]そして、\(g'(0)=-4g_{i-1}-2g_i\ \ g'(1)=2g_{i-1}+4g_i \) となる直線、さらに \( g_{i-1}=0,g_i=0\) となる4本の直線で \(g_{i-1}×g_i\) 平面を下記グラフのように8等分します。
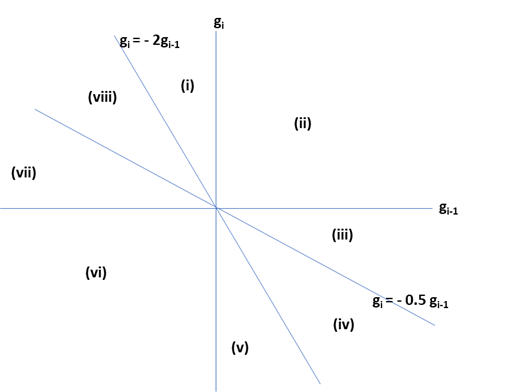
さて、ここで、区間の両端 \(x=0,\ x=1\) における \(g(0),\ g(1),\ g'(0),\ g'(1)\) の正負の組合せを考えます。
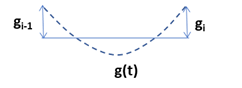
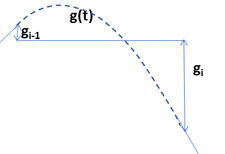
- \(g_{i-1}\lt 0,\ g_i\gt 0\) の場合、必ず \(g'(0)\lt 0,\ g'(1)\gt 0\) になります。上記グラフでは (ii) の領域になります。すなわち、\(g(x)\) の左端の傾きは右下がりで、右端の傾きは右上がりになります。そうすると、\(g(x)\) は区間 \(t\in [t_{i-1},t_i]\) 内で局所的な最小値を取ります。この区間では単調増加・減少になり得ません。
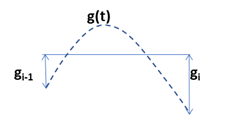
- \(g_{i-1}\lt 0,\ g_i\lt 0\) の場合、必ず \(g'(0)\gt 0,\ g'(1)\lt 0\) になります。上記グラフでは (vi) の領域になります。すなわち、\(g(x)\) の左端の傾きは右上がりで、右端の傾きは右下がりになります。そうすると、\(g(x)\) は区間 \(t\in [t_{i-1},t_i]\) 内で局所的な最大値を取ります。
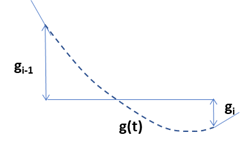
- \(g_{i-1}\lt 0,\ g_i\gt 0\) の場合で、\(g'(0)\gt 0,\) かつ \(g'(1)\gt 0\) の場合に、\(g(t)\) は右上がりの単調増加になります。そして、\(g'(0)=-4g_{i-1}-2g_i\gt 0\) となるのは、\(-2g_{i-1}\gt g_i\) の場合で、\(g'(1)=2g_{i-1}+4g_i\gt 0\) となるのは \(-0.5g_{i-1}\lt g_i\) の場合です。上記グラフでは (viii) の領域になります。
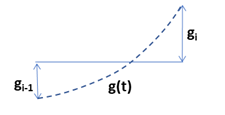
- \(g_{i-1}\gt 0,\ g_i\lt 0\) の場合で、\(g'(0)\lt 0,\) かつ \(g'(1)\lt 0\) の場合に、\(g(t)\) は右下がりの単調減少になります。そして、\(g'(0)=-4g_{i-1}-2g_i\lt 0\) となるのは、\(-2g_{i-1}\lt g_i\) の場合で、\(g'(1)=2g_{i-1}+4g_i\lt 0\) となるのは \(-0.5g_{i-1}\gt g_i\) の場合です。上記グラフでは (iv) の領域になります。
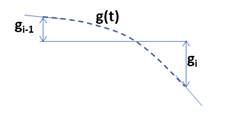
- \(g_{i-1}\lt 0,\ g_i\gt 0\) の場合で、\(g'(0)\gt 0,\) かつ \(g'(1)\lt 0\) の場合に、\(g(t)\) は局所的な最大値を持ちます。そして、 \(g'(0)=-4g_{i-1}-2g_i\gt 0\) となるのは、\(-2g_{i-1}\gt g_i\) の場合で、\(g'(1)=2g_{i-1}+4g_i\lt 0\) となるのは \(-0.5g_{i-1}\gt g_i\) の場合です。上記グラフでは (vii) の領域になります。
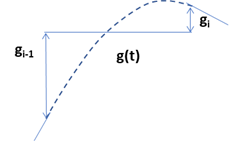
- \(g_{i-1}\lt 0,\ g_i\gt 0\) の場合で、\(g'(0)\lt 0,\) かつ \(g'(1)\gt 0\) の場合に、\(g(t)\) は局所的な最小値を持ちます。そして、\(g'(0)=-4g_{i-1}-2g_i\lt 0\) となるのは、\(-2g_{i-1}\lt g_i\) の場合で、\(g'(1)=2g_{i-1}+4g_i\gt 0\) となるのは \(-0.5g_{i-1}\lt g_i\) の場合です。上記グラフでは (i) の領域になります。
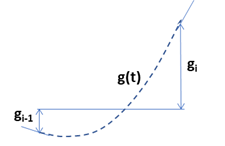
- \(g_{i-1}\gt 0,\ g_i\lt 0\) の場合で、\(g'(0)\gt 0,\) かつ \(g'(1)\lt 0\) の場合に、\(g(t)\) は局所的な最大値を持ちます。そして、\(g'(0)=-4g_{i-1}-2g_i\gt 0\) となるのは、\(-2g_{i-1}\gt g_i\) の場合で、\(g'(1)=2g_{i-1}+4g_i\lt 0\) となるのは \(-0.5g_{i-1}\gt g_i\) の場合です。上記グラフでは (v) の領域になります。
- \(g_{i-1}\gt 0,\ g_i\lt 0\) の場合で、\(g'(0)\lt 0,\) かつ \(g'(1)\gt 0\) の場合に、\(g(t)\) は局所的な最小値を持ちます。そして、 \(g'(0)=-4g_{i-1}-2g_i\lt 0\) となるのは、\(-2g_{i-1}\lt g_i\) の場合で、\(g'(1)=2g_{i-1}+4g_i\gt 0\) となるのは \(-0.5g_{i-1}\lt g_i\) の場合です。上記グラフでは (iii) の領域になります。
さて、このセクションの最初に述べた、単調性の制約を課したいというのは、上の(e) ~ (h) のケースです。前後とあわせて3区間の区間フォワード金利が単調増加・減少しているにもかかわらず、瞬間フォワード金利に局所的な最大値・最小値が発生しているのを、無理やり単調増加・減少になるよう修正を加えるという事になります。
(\(-2g_{i-1}=g_i,\ -0.5g_{i-1}=g_i\) の場合、すなわち\( x=\) 0 または 1 のいずれかで傾きがゼロの場合は、区間の両端のどちらかで最大値あるいは最小値を取り、とりあえず単調性は維持されます。)
< 単調性(Monotonicity)の強制 >
その具体的な方法ですが、Hagan-Westは、瞬間フォワード金利のカーブに無理やり直線部分を導入して操作する方法を提示しています。
まず、上記の (f) の場合で局所的な最小値が発生する場合、左端から一定区間 \(x\in [0,\eta ]\) の値を \(g_{i-1}\) とし、そこから先を\(x\) の2次関数とします。その場合、\(g(x)\) の平均が 0 になるように ( \(g(x)\) の 0 から 1 までの積分が 0 になるように)、直線区間(ηの値)を決めます。すなわち
\[ g(t)=\begin{cases} g_{i-1},\ \ \ \ \ \ \ for\ 0\lt x \lt \eta\\ g_{i-1}+(g_i-g_{i-1})\left( \frac{x-\eta}{1-\eta}\right) ^2\ \ for\ \eta\lt x \lt 1 \end{cases} \tag{1.1.51} \] \[ \eta =1+3 \frac{g_{i-1}}{g_i-g_{i-1}}=\frac{g_i+2g_{i-1}}{g_i-g_{i-1}},\ \tag{1.1.52} \]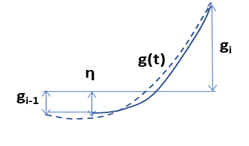
また、上記 (e) の場合で局所的な最大値が発生する場合、右端から一定区間(\(x\in [\eta,1]\)) の値を \(g_i\) とし、そこまでを \(x\) の2次関数とします。その場合、\(g(x)\) の平均が 0 になるように(\(g(x)\) の 0 から 1 までの積分が 0 になるように)、直線区間(ηの値)を決めます。すなわち
\[ g(t)=\begin{cases} g_i+(g_{i-1}-g_i)\left( \frac{\eta -x}{\eta}\right) ^2\ \ for\ 0 \lt x \lt \eta\\ g_{i-1},\ \ \ \ \ \ \ for\ \ \eta \lt x \lt 1 \end{cases} \tag{1.1.53} \] \[ \eta =3 \frac{g_i}{g_{i-1}-g_i},\ \tag{1.1.54} \]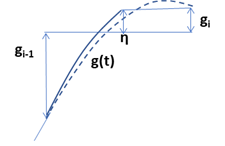
同様に、(g)(h)の場合も、直線部分を加えて、局所最大値・最小値が、\(g_{i-1},\ g_i\) を超えないようにします。
さらに、(a)のケースでも修正を加えます。(a)では、\(g_{i-1}\gt 0,\ g_i\gt 0\) なので局所最小値が発生するのはやむを得ないですが、\(g_{i-1}→0,\) または \(g_i→0,\) の場合、Interpolatorが、突如、2次関数の曲線から直線(区間全体で\(g_{i-1}\) または\(g_i\) の値を取る直線)になってしまいます。そこで、Interpolatorを、[0,1] 間の点 η において、最小値Aとなる2本の2次関数を接続させる形を取ります。すなわち
\[ g(x)=\begin{cases} A+(g_{i-1}-A)\left( \frac{\eta -x}{\eta }\right)^2\ \ \ for\ 0\lt x \lt \eta\\ A\ \ \ \ for\ x=A\\ A+(g_i-A) \left( \frac{x-\eta}{1-\eta}\right)^2 \ \ \ for\ \eta \lt x \lt 1 \end{cases}\ \tag{1.1.55} \]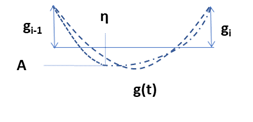
ηとAをどうやって決めるかですが、まず、Aの値は、\(g(t)\) の平均が 0 (2本の2次関数をそれぞれ[0,η] [η,1]の区間で積分した合計)という条件から、次のようになります。
\[ A=-\frac{1}{2}(\eta g_{i-1}+(1-\eta)g_i),\ \tag{1.1.56} \]またηは、\(g_{i-1}→0,\) または \(g_i→0,\) の場合、Interpolatorが直線になる必要があるので次の様な制約がかかります。
\[ \eta =\begin{cases} 1,\ \ if\ g_{i-1}=0\\ 0,\ \ if\ g_i=0 \end{cases}\ \ \tag{1.1.57} \]これらを満たすηとAは、次の様になります。
\[ \eta =\frac{g_i}{g_i+g_{i-1}}, \tag{1.1.58} \] \[ A=-\frac{g_i g_{i-1}}{g_i+g_{i-1}}, \tag{1.1.59} \]1.1.6.4 \(f(t)\) がマイナス金利にならないような修正
Hagan-Westは、上記のような修正に加え、f(t)がマイナスにならないような方法も提示しています。マイナス金利は、日本や欧州では、もはや異常値で無くなっており、あえて修正は必要ないかも知れませんが、とりあえずHagan-Westの修正を簡単に説明しておきます。
まず、区間フォワード金利が、全区間でプラスであると仮定します。区間フォワード金利が仮にマイナスの区間がある場合、もはや修正の余地はありません。市場データそのものが、将来のマイナス金利を予想しているとして、受け入れるしかありません。区間フォワード金利がプラスである限り、このMonotone Convex Spline法では、各Pillarにおける瞬間フォワード金利は、必ずプラスになります。最初に仮定した、各Pillarにおける瞬間フォワード金利の推定方法の1.1.38式を見れば明らかです。
\[ f_i=\frac{t_i-t_{i-1}}{t_{i+1}-t_{i-1}} f_{i+1}^d+\frac{t_{i+1}-t_i}{t_{i+1}-t_{i-1}} f_i^d,\ \ for\ i=1,2,…,n-1\ \tag{1.1.38} \]\(g_{i-1},\ g_i,\ g'(0),\ g'(1)\) の正負により、\(g_{i-1}\times g_i\) 平面を8分割したグラフを再度見て下さい。ここで、局所的な最小値が発生する領域は、(i) (ii) (iii)の3領域です。(i) (iii)の場合は、瞬間フォワード金利の最小値は、上記の直線による修正を加える事によって、それぞれ、\(f_{i-1},\ f_i\) になり、プラスのままです。(ii)の場合の瞬間フォワード金利の最小値は、\( f_i^d-\frac{g_i g_{i-1}}{g_i+g_{i-1}} \) になり、これがマイナスにならないようにします。
その為には、区間 \([t_{i-1},\ t_i]\) の両側のPillarにおける瞬間フォワード金利 \(f_{i-1},\ f_i\) が、\(0 \lt f_{i-1} \lt 3f_i^d,\ 0\lt f_i \lt 3f_i^d\) となることが必要です。(ii)の領域では、\(f_{i-1} \gt f_i^d,\ f_i\gt f_i^d\) ですが、\(f_i^d\) の3倍以上大きくならないように修正を加えれば、区間最小値がマイナスになりません。
Hagan-Westは、0にあまり近づかないようにする為に、もう少し条件を厳しくし
\[ 0\lt f_{i-1} \lt 2f_i^d,\ 0\lt f_i\lt 2f_i^d, \]とうい条件を提案しています。すなわち、各 \(f_i,\ i=0,1,…,n\) について
\[ f_0 → bound (0,\ f_0,\ f_1^d)\\ f_i → bound (0,\ f_i,\ 2 \min(f_i^d,\ f_{i+1}^d))\\ f_n → bound (0,\ f_n,\ f_n^d) \]という制約条件を課せば、Interpolatorは、かならず正の値を取る事になります。(カーブの両端では0を許容しています。)
各Pillarにおける瞬間フォワード金利は、最初は機械的に、前後の区間フォワード金利の加重平均に決めますが、仮にそれが区間フォワード金利の2倍以上の値になった場合は、無理やり2倍までに下方修正するものです。
以上が、Forward Monotone Convex Spline法です。この方法で描かれた瞬間フォワード金利のカーブは、これまでのどの方法よりも、不自然な波や、大きな”たわみ”が消え、自然に見えます。同じ様に波やたわみを軽減させる方法でも、Tension Spline法のように、主観的なσやλといった係数を外生的に与える必要がなく、決まったアルゴリズムでカーブを構築できます。さらに、Spline関数の係数は、Pillar前後の区間フォワード金利のみを使うので、局所性にも優れています。しかし、相当技巧的な方法であり、カーブに直線部分が発生するなど、無理やり修正している感があります。
1.1.6.5 Forward Monotone Convex Spline法のさらなる修正
Hagan-Westは、上記のForward Monotone Convex Spline法について、さらなる修正を加えたアイデアを提示しています。すなわち、上記の方法は、Interpolatorに直線部分が発生する可能性があり、あまり滑らかではありません。そこで、各Pillarにおける瞬間フォワード金利の値を、一定の範囲内に制限する事で、出来るだけそれを避けようとするものです。
前の方法を、さらに技巧的に修正を加えるもので、出来上がった瞬間フォワード金利カーブは、さらに見栄えはよくなりますが、無理やり感はさらに強くなります。
瞬間フォワード金利のカーブは、その積分値が、Pillar間の区間フォワード金利と同じになるというのが絶対条件で、各Pillarでは、どのような値も取り得ます。であれば、他にも修正方法はいくらでも考え得るので、最終的にはカーブの見栄えが良くなるようなInterpolatorはいくらでも作れます。具体的な方法については、説明を省略したいと思いますので、興味のある方はHagan-Westの論文を参照して下さい。
1.1.6.6 瞬間フォワード金利から、Zero Rateを導出
Forward Monotone Convex Spline法は、原データとして、区間フォワード金利が既知として、そこから瞬間フォワード金利のInterpolatorを導出しました。区間フォワード金利が既知という事は、各PillarにおけるZero Coupon Rateも既知という事になります。しかしPillar間でのZero Coupon Rateは、瞬間フォワード金利のカーブから導出する必要があります。Pillar \(t_{i-1}\) におけるZero Coupon Rateが既知で、それを \(r_{i-1}\) とします。区間 \([t_{i-1},\ t_i]\) におけるZero Coupon Rateを \(r(t)\) とすると、
\[ r(t)t=r_{i-1}t_{i-1}+\int_{t_{i-1}}^t f(s)ds=r_{i-1}t_{i-1}+(t-t_{i-1})f_i^d+\int_{t_{i-1}}^t g(s)ds,\ \tag{1.1.60} \]の等式が導けます。また、\(g(x)\) は下記式で、\(g_{i-1},\ g_i\) と \(x(t)=\frac{t-t_{i-1}}{t_i-t_{i-1}}\) で表現できます。
\[ g(x(t))=g_{i-1}(1-4x+3x^2 )+g_i(-2x+3x^2 ),\ \ x\in [0,1]\ \tag{1.1.61} \]従って、\(g(x)\) の \(t_{i-1}\ から\ t\) までの積分は下記のようになります。
\[ \int_{t_{i-1}}^t g(s)ds=\int_{t_{i-1}}^t [g_{i-1} (1-4x(s)+3x(s)^2)+g_i(-2x(s)+3x(s)^2)]ds\\ =(t_i-t_{i-1})\left[ g_{i-1} (x-2x^2+x^3)+g_i(-x^2+x^3 )\right] ≡I_t, \tag{1.1.62} \]結果、期間 \(t\) におけるZero Coupon Rateは
\[ r(t)=\frac{1}{t}\left( r_{i-1} t_{i-1}+(t-t_{i-1}) f_i^d+I_t \right), \tag{1.1.63} \]となります。t時のZero Coupon Rateが判れば、そこからDiscount Factorや、任意の区間の区間フォワード金利も求まります。