上級編 5. マルコフ汎関数モデル
5.3 ニュメレール価格の確率分布の導出法
5.3.3 マルコフ汎関数モデルによるデジタルオプション価格の導出
次に、MFMで、5.3.2 で求めたデジタルオプション価格と同じ価格になるデジタルオプションのストライク \(x_K\) を求めます。これは、フォワードスワップ金利 S の確率分布(市場データに内包している Volatility Smile の形状を持った分布)を、正規分布する x の座標に Mapping(写像)する操作になります。グラフにすると、下記のような対応関係を求める操作になります。
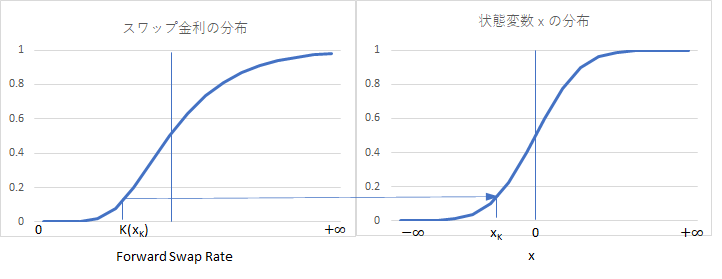
フォワードスワップ金利の分布は、おおむね対数正規分布ですが、Volatility Smile があるので、そこから若干ずれた形になります。対数正規分布なので、下限は 0% で、上限は +∞ です。対数正規分布であれば、分布は平均よりプラス側に大きく広がっています。それに対し、正規分布する x の分布は、−∞ から +∞ の範囲で広がり、確率 0.5 に対応する x は 0 で、分布は プラスーマイナスで対象になります。
行おうとしている事は、デジタルオプションのストライクKに対応する、状態変数 \(x_K\) を探す事です。それは即ち、フォワードスワップ金利 S が K を下回る確率と同じ確率となる x を求める事になります。(先ほど \(Φ^* (S(T_i,T_i,T_n) < K)\) が K に対して単調増加関数である必要性を述べましたが、この対応関係を求める為に必須です。)
その為に、MFM を使って、\(x_K\) をストライクとするデジタルオプション価格を計算します。まず Payoff は、次のように表現できます。
\[ Annuity(T_i,T_i,T_n )~I(x_{T_i} < x_K ) \]そして、ニュメレールに対応する確率測度を使えば、5.4 式から、現時点(t=0)における MFM でのデジタルオプション価格は下記式のようになります。
\[ DigitalPrice_{MFM}=N(0,T_n) E^{Q_N} \left[ \frac{Annuity(T_i,T_i,T_n,x_{T_i})}{N(T_i,T_n,x_{T_i})} I(x_{T_i} < x_K )~|~x_0=0 \right] \tag{5.12} \]右辺の期待値演算は、x の確率密度関数を使って、[ ]内の Payoff を積分して導出します。x がガウス分布すると仮定しているので、密度関数は解析的に求まります。また \( \frac{Annuity(T_i,T_i,T_n,x_{T_i})}{N(T_i,T_n,x_{T_i})}~ は、T_n\) から時間軸を遡りながら求めていきます。\(N(0,T_n)\) は当初イールドカーブから求まります。従って、時間軸を遡る事によって、すべての時間軸について 5.12 式が計算できます。そのアルゴリズムの詳細は後ほど説明します。
そして、この価格が、先ほどの市場データから導出されるデジタルオプション価格式(5.7式)と一致するようにすれば、K と \(x_K\) の対応関係、すなわちフォワード金利の分布を x に対応付ける事ができます。要は、下記方程式を満たす\( K~ と~ x_K\) の対応関係を探す事になります。
\[ \begin{align} N(0,T_n ) E^{Q_N} & \left[ \frac{Annuity(T_i,T_i,T_n,x_{T_i} )}{N(T_i,T_n,x_{T_i})} I(x_{T_i} < x_K)~|~ x_0 \right] \\ & =Annuity(t_0,T_i,T_n) E^{Q_A} \left[ I(S(T_i,T_i,T_n) < K)~|~S_0 \right] \tag{5.13} \end{align} \]