2. "Implementing QuantLib"の和訳
Chapter VIII The Finite-Difference Framework (有限差分法のフレームワーク)
8.2 The New Framework (新しいフレームワーク)
8.2.1 Meshers : メッシャー (離散化した確率変数の格子)
(上記価格エンジンの calculate( )メソッドの中で) 最初に生成される部品(component)は Fdm1dMesherクラスのインスタンスで(正確に言えば、その派生クラスであるFdmBlackScholesMesherクラスのインスタンスです)、そのインターフェースを下記 Listing 8.18 に示します。Fdm1dMesherのインスタンスは、方程式が定義されている1次元領域を、離散化して保持します。Listing8.17で示した価格エンジンは対象資産1個のオプション用なので、対象資産価格の取り得る領域をモデル化するには、このインスタンスが1つあれば十分です (訳注:マルチファクターモデルであれば、Fdm1dMesherインスタンスをファクター数だけ用意する必要がある)。
Listing 8.18:Fdm1dMesherクラスのインターフェース
class Fdm1dMesher {
public:
Fdm1dMesher(Size size);
Size size() const;
Real dplus(Size index) const;
Real dminus(Size index) const;
Real location(Size index) const;
const std::vector<Real>& locations();
protected:
std::vector<Real> locations_;
std::vector<Real> dplus_, dminus_;
}; このベースクラスは、いくつかのインスペクター関数以外は、何の動作も行いません。メンバー変数として locations_ という名前の配列を保持していますが、そこには \(x\) (訳注:ここでは対象資産の価格(の対数)) の領域を離散化した \( \{ x_0,x_1,…..,x_{n-1} \}\) という点の集合が格納されます。同時に、後の計算で便利なように、2つの配列、dplus_ と dminus_ を事前計算して格納しており、そのi番目の要素にはそれぞれ \( (x_{i+1}-x_i )\ と\ (x_i-x_{i-1})\) の値が入ります。これらの値の事前計算は、派生クラスのコンストラクターが行うので、protectedとして宣言されています。
このクラスのインスタンスが生成される際は、通常 shared_ptr として、(他のオブジェクトと)共有される事を想定して生成されています。しかしこのクラスはpolymorphicではありません。このクラスのどのインターフェースも仮想関数ではありません。 (注:このクラスは、仮想デストラクターさえ持っていません。その為、ベースクラスへのポインターが消去された場合、予想外の動作が起こる可能性があります。その場合でも、shared_ptrのコンストラクターのおかげで、大丈夫です。shared_ptrは、与えられたポインターの型に応じて、正しい消去機能を備えているからです。)
実際の所、このインスタンスをポインターとして(他のオブジェクトに)渡す必然性は、おそらく勝手なコピーを避ける為以外には、無いように思えます。コピーでさえ問題ないかも知れません (仮に C++11 のモードでコンパイルするなら、その問題が起こることさえないでしょう) 後から見れば、Fdm1dMesherクラスは、継承を伴わないクラスとして作ることが出来たかもしれません。その場合は、派生クラスの役割を、Fdm1dMesherインスタンスを生成したり返したりする関数群で置き換えればいいでしょう。
上記の Listing 8.18 には載せていませんが、(Fdm1dMesherの派生クラスである) FdmBlackScholesMesher のコンストラクターは、いくつかの事前計算を行っています。まず、オプション対象資産の現在の価格、現時点からオプション期日までの分散値、および幾つかの外生的な制約条件(例えば、バリアなど)をもとに、価格グリッドの境界値を決めています (訳注:対象資産価格が取り得る最大値と最小値。オプション価格の境界条件では無い)。その境界値は、この価格エンジンだけで使われるのではなく、対象資産が、同じ確率過程を取る、他のオプションでも使う事を意図して作られています。計算方法は、古いフレームワークにおける FDVanillaEngineクラスで実装されているものと似ていますが、新しいプログラムでは、ユーザーがいくつかのパラメータ(古いフレームワークでは Hard-cord されていたもの)を調整できるようにしています。価格グリッドについては、古いフレームワークと同様、対象資産価格の対数を離散化しています。
境界値を計算した後、コンストラクターは、実際の価格グリッドの構築作業を、Fdm1dMesherクラスから派生した2つの汎用的なユーティリティークラスに委託しています。そして、そこで計算されたデータをメンバー変数にコピーします。もし、先ほど述べたように、(派生クラスで動作を実装するのではなく) Fdm1dMesherクラス内で関数を実装して動作を完結させたいのなら、その関数群は、構築された価格グリッド(価格のメッシュ)を返すようにすればいいでしょう。
その2つのユーティリティークラスの内、シンプルな方は、Uniform1dMesherクラスと名付けられており、その名前が示す通りの動作を行います。すなわち、引数で取ったグリッドポイント数を基に、2つの境界点の間に等間隔のグリッドを構築します。
もう一つのクラスは、Concentrating1dMesherクラスと名付けられており、グリッドポイントの中で、特別なポイントがひとつ、あるいは複数ある場合 (例えばストライク価格など) に、使われます。そのコンストラクターは、引数で与えられたグリッド数を基にグリッドを構築しますが、その際、いわゆるcritical points(グリッド生成上、重要なポイント)のまわりにグリッドポイントが集中するように構築します。各 critical points について、コンストラクターは、引数として、①ciritical pointsの値、②ポイントの周辺にグリッドを集中させる場合の密度、③critical points をメッシュポイントに含めるかどうかのフラッグ、を取ります (訳注:3番目の引数は、Listing8.17の中の FdmBlackScholesMesherのコンストラクターでは、引数として指定されていません。実際の QuantLibのコードを確認しましたが、コンストラクターは、そのような引数を取っておらず、①と②の引数がNullでないかどうかで判断しています。おそらく著者の勘違いかと思います)。
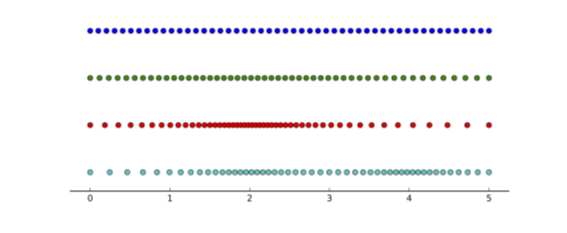
下の図は、このコンストラクターを使った場合に、どのようなメッシュが構築されるかを示しています。一番上から順番に、①均一なメッシュ、②x=2をcritical pointとした集中メッシュ、③x=2をcritical pointとした集中メッシュでその周辺の密度をさらに上げたメッシュ、④x=2と x=4をcritical pointとした集中メッシュ、になります。すべてのメッシュについて、ポイント数は同じです。
多次元の状態変数を持つ有限差分モデル用のメッシュは、FdmMesherクラスで抽象化されており、そのインターフェースを下記 Listing 8.19 に示します。このセクションの最初に示した価格エンジンのプログラムコードの中では、このクラスの派生クラスである FdmMesherCompositeクラスをインスタンス化して使っています (同様に下記 Listing に示しています)。このクラスは方程式中の状態変数ごとに1次元のメッシュ(Fdm1dMesher)を構築しています。上記価格エンジンの例は、対象資産価格のメッシュインスタンスをひとつだけ生成しています。
Listing 8.19:FdmMesherクラスとFdmMesherCompositeクラスのインターフェース
class FdmMesher {
public:
FdmMesher(const shared_ptr<FdmLinearOpLayout>&);
virtual ~FdmMesher() {}
virtual Real dplus(const FdmLinearOpIterator& iter,
Size direction) const = 0;
virtual Real dminus(const FdmLinearOpIterator& iter,
Size direction) const = 0;
virtual Real location(const FdmLinearOpIterator& iter,
Size direction) const = 0;
virtual Array locations(Size direction) const = 0;
const shared_ptr<FdmLinearOpLayout>& layout() const;
};
class FdmMesherComposite : public FdmMesher {
public:
explicit FdmMesherComposite(
const shared_ptr<Fdm1dMesher>& mesher);
FdmMesherComposite(
const shared_ptr<Fdm1dMesher>& m1,
const shared_ptr<Fdm1dMesher>& m2);
// ... constructors for up to 4 meshers ...
explicit FdmMesherComposite(
const std::vector<shared_ptr<Fdm1dMesher> >&);
Real dplus(const FdmLinearOpIterator& iter,
Size direction) const;
Real dminus(const FdmLinearOpIterator& iter,
Size direction) const;
Real location(const FdmLinearOpIterator& iter,
Size direction) const;
Array locations(Size direction) const;
}; 残念ながら、この多次元用のFdmMesherクラスのインターフェースについて十分に説明しようとすると、相当ややこしい内容にまで入り込まなければなりません。考え方だけを言えば、これらのメソッド群は、(何等かのIteratorによって特定される) 多次元のメッシュ上の特定のポイントにおいて、その location の値と、その点から指定された次元軸方向への差分 (dplusと dminus) を取りだす事ができます。しかし、より明確に理解するには、まず多次元の Operator(差分演算子)と配列をどう表現するかについて見てみる必要があります。
<ライセンス表示>
QuantLibのソースコードを使う場合は、ライセンス表示とDisclaimerの表示が義務付けられているので、添付します。 ライセンス