上級編 4. Short Rate Models
4.4 Hull-White モデル
4.4.5 Trinomial Tree : 3項ツリーの構築
4.4.5.3 3項ツリー構築のアルゴリズム(続き)
4.4.5.3.6 \(x\) の樹形構造から、瞬間短期金利 \(r\) の樹形構造へ変換
以上で、\(x(t)\) の樹形構造が完成したので、それを元の \(r(t)\) の樹形構造へ戻す必要があります。まず、\(r~~を~~x\) に変換した式を再記します。
\[ r(t)=x(t)+ϕ(t)~~~~~~ \\ x(0)=0,~~~~~~~r(0)=ϕ(0) \]Hull-White モデルにおける、中心回帰レベルのパラメータ \(θ(t)\) の役割を、上の式の \(\phi (t)\) が担います。すなわち、\(\phi (t)\) を使って、\(r\) の3項ツリーの構造が当初イールドカーブに完全にフィットするようにします。当初イールドカーブに完全にフィットするとは、以下に説明する通り、3項ツリーが近似する、瞬間短期金利の確率過程から導出されるゼロクーポン債価格が、当初イールドカーブと完全に一致する事を意味します。
もともとShort Rate Modelは、現在のゼロクーポン債価格(すなわち Discount Curve)と、瞬間短期金利の確率過程の関係が、リスク中立測度下で、下記のようになると仮定しています。
\[ P(0,T)=E^{Q_{RN}} \left( e^{-\int_0^T r(u)du} \right) \]3項ツリーは、\(r(t)\) の(連続な)確率過程を、離散的に近似したものなので、上式の関係を離散時間で書き直し、さらに \(r(t_i)=x(t_i)+ϕ(t_i)\) の関係式を代入すると
\[ \begin{align} P(0,T) & =E^{Q_{RN}} \left(e^{-\sum_{i=0}^{N-1} r(t_i)Δt_i} \right) \\ & =E^{Q_{RN}} \left( e^{-\sum_{i=0}^{N-1} (x(t_i )+ϕ(t_i))Δt_i} \right),~~~~t_N=T \tag{4.48} \end{align} \]の関係式が導けます。左辺の \(P(0,T)\) は現時点の T 満期のゼロクーポン債価格(すなわち現時点の Discount Curve)で、市場データから与えられます。一方、右辺の \(x(t_i)\) の値と、そこへ到達する確率は、3項ツリーの構造から既に求まっています。従って、未知数は \(\phi(t_i)\) のみになります。その \(\phi (t_i)\) の値は、\(\phi (0)\) から帰納的に、ツリー構造を前進しながら求める事ができます。では具体的にそのアルゴリズムを見てみます。
(i) \(t_0\) 時および \(t_1\) 時の Arrow Debreu 価格と、\(\phi (0)\) を市場データから求める
まず、最初に3項ツリーの各ノード座標 \((i,j)\) に到達した場合にだけ 1 を支払うゼロクーポン債価格の現在価値を \(Q_{i,j}\) と定義します。いわゆるArrow-Debreu 価格と呼ばれているものです。この \(Q_{i,j}\) は、言い換えると、利回りが、\((i,j)\) ノードに到達するまでの短期金利の累積運用リターン \( \sum_{i=0}^{n-1} r(t_i) Δt_i\) になるゼロクーポン債価格に、そのノードへの到達確率を掛けた値です。要は、4.48 式の右辺の括弧内の値に、各ノードへの到達確率をかけたものです。この \(Q_{i,j}\) を、特定の時間軸 \(t_i\) 上にあるすべてのノード \((j=-m,…0,…m)\) で合計すれば 4.48 式の右辺の期待値を求めた事になります。
まず、\(t_0=0\) 時では、\(P(0,0)=Q_{0,0}=1\) です。また、\(r(0)=r_0=x_0+ϕ(0)\) となります。しかし、まだ \(\phi(0)\) が特定されていないので、\(r(0)\) は特定できません。\(r(0)\) は、現時点のイールドカーブの一番手前(短期)の金利を使えば良さそうに見えますが違います。
(注: \(r(0)~は、t=0\) 時の瞬間短期金利ではありません。モデルを離散化したので、 \(r_{0,0}= r(0)\) は、\(Δt_0\) 間の \(r\) の平均を意味します。これは \(t_1\) 満期のゼロクーポン債の連続複利利回りに相当します。ツリー上の各 \(r_{i,j}\) も、そのノードでの瞬間短期金利ではなく、\(Δt_i\) 間の \(r\) の平均を意味します。ほとんどの文献でこの説明がないので、間違えてオーバーナイト金利を \(r(0)\) として使わないようにして下さい。)
ここで、\(t_1\) 時の各ノード上で満期となるゼロクーポン債価格は、\(r_{0,0}=r(0)\) を使って \(e^{-r_{0,0} Δt_0} \) で求まります。すると、\(t_1\) 軸上の各ノードの \(Q_{1,j}\) は、下記式で求まります。
\[ \begin{cases} & Q_{1,1}=p_{0,0,up}×e^{-r_{0,0}Δt_0} = p_{0,0,up}×e^{-\phi (0)Δt_0} \\ & Q_{1,0}=p_{0,0,mid}×e^{-r_{0,0}Δt_0}= p_{0,0,mid}×e^{-\phi (0) Δt_0} \\ & Q_{1,-1}=p_{0,0,down}×e^{-r_{0,0}Δt_0}= p_{0,0,down}×e^{-\phi (0) Δt_0} \tag{4.46} \end{cases} \]遷移確率は、xのツリーのそれを使います。さらに、右辺をすべて足し上げると、\(e^{-r_{0,0}Δt_0}\) の期待値になり、\(P(0,t_1)\) と一致します。
\[ \sum_{j=-1}^1 Q_{1,j}=E^{Q_{RN}} \left( e^{-r(0) Δt_0} \right) =E^{Q_{RN}} \left( e^{-\phi (0)Δt_0}\right) =P(0,t_1), ~~~~j=-1,0,1 \tag{4.50} \]この式は、\(\phi (0)\) を未知数とする 1 元の方程式であり、これを解けば、\(\phi (0)\) が求まります。さらに \(x(0)+φ(0)\) から r(0) も求まります。ただ、この段階では方程式を解くまでもなく、\(P(0,t_1)\) の利回りがそれです。
以上のロジックを図示したものを下記します。
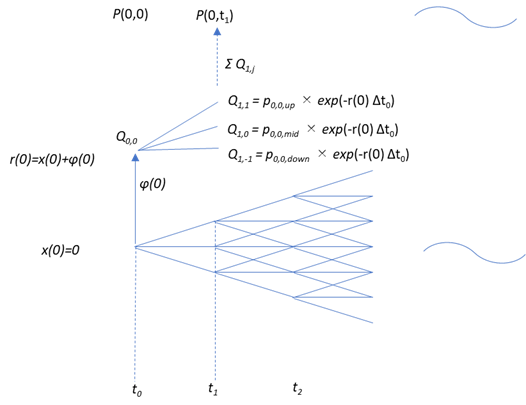
これで、\(t_0~~軸上の~~ r_{0,0},~~ϕ(0),~~Q_{0,0}~~ および~~ t_1~~軸上の Q_{1,1},~~Q_{1,0},~~Q_{1,-1}\) が求まりました。
(ii) \(t_2\) 時の Arrow Debreu 価格と、\(\phi(t_1)\) を求める
次に、\(t_1~軸上の~~r_{1,1},~~r_{1,0},~~r_{1,-1},~~\phi(t_1),~~および~~t_2~軸上の~~Q_{2,2},~~Q_{2,1},~~Q_{2,0},~~Q_{2,-1},~~Q_{2,-2}\) を求めます。(実質的に、求める未知数は \(\phi(t_1)~~のみで、他はすべて~~x_{1,j},~~\phi(t_1),~~p_{1,j,**}\) を使って簡単に計算できます。)
その為に、再度、4.48 式の関係式を使います。4.48 の \(\sum\) の計算を \(i=0,1\) で行うとして書き換えると
\[ P(0,t_2)=E^{Q_{RN}} \left(e^{-\sum_{i=0}^1 r(t_i)Δt_i}\right) = E^{Q_{RN}} \left(e^{-∑_{i=0}^1 (x(t_i)+\phi (t_i))Δt_i} \right), \]その様子を、下記の図を参考にしながら見ていきます。
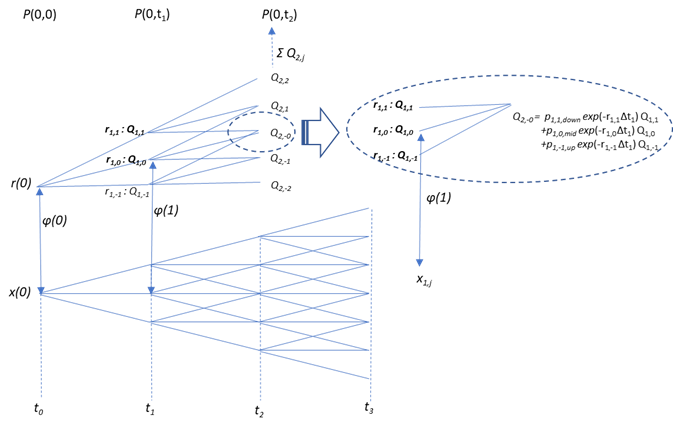
例えば、\(t_2\) の時間軸上の、(2,0) のノードを見てみます。図にある通り、\(t_1\) 軸上のノードから、このノードに到達するルートは3本あります。すなわち(1,1), (1,0), (1,-1) からです。ルートごとの短期金利はそれぞれ \(r_{1,1},~~r_{1,0},~~r_{1,-1}\) になります。すると、このノード上での、\(t_2\) 満期のゼロクーポン債価格は、到達ルートごとにそれぞれ、\(e^{-(r_{0,0}Δt_0~+~r_{1,1} Δt_1)},~~e^{-(r_{0,0} Δt_0~+~r_{1,0} Δt_1)},~~e^{-(r_{0,0} Δt_0~+~r_{1,-1} Δt_1)}\) となります。この値に、ルートごとの到達確率を掛けて合計すれば、\(Q_{2,0}\) の価格になります。式で表現すると下記のようになります。
\[ \begin{align} Q_{2,0}= ~& p_{0,0,up}× p_{1,1,down} × e^{-(r_{0,0}Δt_0~+~r_{1,1} Δt_1)} \\ + & p_{0,0,mid}×p_{1,0,mid}× e^{-(r_{0,0} Δt_0~+~r_{1,0}Δt_1)} \\ + & p_{0,0,down}×p_{1,-1,up}× e^{-(r_{0,0} Δt_0~+~r_{1,-1}Δt_1)} \end{align} \]この式の右辺の各項にある、\(p_{0,0,*} \times e^{-r_{0,0} Δt_0}\) の部分(式を注意深く見て下さい)は、すでに \(Q_{1,1},~~Q_{1,0},~~Q_{1,-1}\) として求まっているので、それを代入します。すると、
\[ \begin{align} Q_{2,0} = & Q_{1,1} × p_{1,1,down} e^{-(r_{1,1} Δt_1)} \\ + & Q_{1,0}×p_{1,0,mid} e^{-(r_{1,0}Δt_1)} \\ + & Q_{1,-1}×p_{1,-1,up} e^{-(r_{1,-1}Δt_1)} \\ ~\\ = & Q_{1,1}×p_{1,1,down} e^{-(x_{1,1}+\phi(t_1))Δt_0} \\ + & Q_{1,0}×p_{1,0,mid} e^{-(x_{1,0}+\phi (t_1))Δt_0} \\ + & Q_{1,-1}×p_{1,-1,up} e^{-(x_{1,-1}+\phi (t_1))Δt_0} \tag{4.51} \end{align} \]となります。
同様の方法で、\(t_2\) 軸上のすべての \(Q_{2,j}\) の式が導出できます。これを足しあげたものが、\(E^{Q_{RN}} \left(e^{-\sum_{i=0}^1 (x(t_i) + \phi (t_i))Δt_i} \right)\) に相当し、それが \(P(0,t_2)\) に一致します。 各 \(Q_{2,j} は \phi (t_1) \) を未知数とする関数と見做せます。それを \(Q_{2,j} (\phi (t_1))\) と表記し、足し上げると、下記の1元の方程式を立てる事ができます。
\[ P(0,t_2)=\sum_{j=-2}^2 Q_{2,j}(\phi(t_1)) \tag{4.52} \]この式は、1次元のSolverを使って、簡単に解く事ができます。これで \(\phi(t_1)\) が求まりました。\(t_1~軸上の~~r_{1,1},~~r_{1,0},~~r_{1,-1},~~および~~t_2~軸上の~~Q_{2,2},~~Q_{2,1},~~Q_{2,0},~~Q_{2,-1},~~Q_{2,-2}~~は~~\phi(t_1)~~から簡単に導出できます。\) 、
(iii) 同じアルゴリズムを使い \(t_3\) 以降の Arrow Debreu 価格と、\(t_2\) 以降の \(\phi(t_i)\) を求める。
以上のアルゴリズムを、時間軸を1つずつ前進させ、すべての時間軸で行えば、\(\phi(t_i),~~~i=0,~1,~…~,~N-1\) が求まり、\(x_{i,j}\) にそれを加える事で、\(r(t)\) の3項ツリーが完成します。同時にノード間の遷移確率もすべて求まります(\(x\) の樹形構造で求めた遷移確率が、そのまま当てはまります)。
完成した3項ツリーのイメージは、(大分省略していますが)下記のようなものになります。
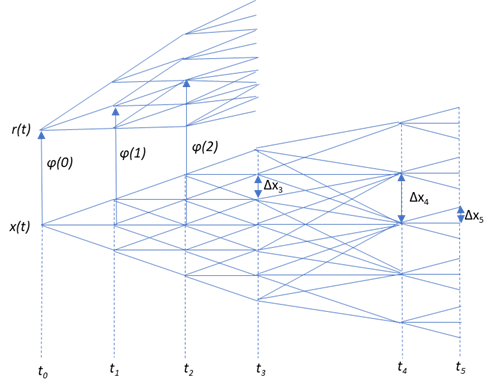
< \( Q_{i,j}~~ と~~ \phi(t_i)\) を求めるアルゴリズムについて >
私の知る限り(と言っても、大した事ないですが)、3項ツリー構築のアルゴリズムを解説している文献は、すべて Arrow Debreu 価格である \(Q_{i,j}\) を求める式を使って Fitting(調整)パラメータ \( \phi (t_i)\) を導出しています。そこでは、Arbitrage Freeの条件を満たす式である
\[ P(0,t_n)=E^{Q_{RN}} \left(e^{-\sum_{i=0}^{n-1} r(t_i)Δt_i} \right) =E^{Q_{RN}} \left(e^{-\sum_{i=0}^{n-1} (x(t_i)+\phi(t_i))Δt_i)} \right), \]を使って、\(\phi(t_i)\) の方程式を立て、Solver を使ってその解を求めています。上式の括弧内を、すべてのノードで計算し、それにそのノードへの到達確率を掛けた値が \(Q_{i,j}\) になります。
しかし、上記の式の左辺をゼロクーポン債価格ではなく、その連続複利利回り(ここでは年率 \(R(0,t_i)\) と表記します)を使っても \(\phi(t_i)\) の方程式を立てる事は可能です。すなわち
\[ R(0,t_n)t_n=E^{Q_{RN}} \left(\sum_{i=0}^{n-1} r(t_i)Δt_i \right) =E^{Q_RN} \left(\sum_{i=0}^{n-1} (x(t_i)+\phi(t_i))Δt_i \right), \tag{4.53} \]でもいいのではないかと思います。こうすれば、右辺の期待値演算の括弧内から指数関数の演算が消えます。指数関数は、コンピューターでも比較的時間のかかる演算であり、それをSolverの中で繰り返し演算すると、計算負荷は相当大きくなります。この式の意味も明瞭です。すなわち3項ツリー上の短期金利で運用を繰り返したリターンの、リスク中立測度下での期待値は、長期金利のリターンと一致するというものです。