上級編 6. Libor Market Model
6.3 古典的なLMMの拡散項係数(Volatility関数)
6.3.3 Volatilityの期間構造 (Term Structure of Volatility)
フォワード Libor の Volatility の期間構造は、基本的に Cap/Floor 価格に内包されています。Cap・Floor は、複数の、独立した、すべて同じストライクレートを持つ Caplet・Floorlet の集合です。Cap を構成する各 Caplet は、それぞれフォワード Libor を対象金利とする、Payer タイプのヨーロピアンオプションです。 (同様に Floor は Receiver タイプの金利オプションである Floorlet の集合) 同じストライクレートを持つ、期間の異なる Cap のシリーズから、Bootstrapping-Interpolation の要領で、個々の Caplet 価格が導出でき、そこから Implied (Black)Volatility も導出できます。それを、対象 Libor の期間の順番に並べたのが、Volatility の期間構造になります。
しかし注意する点は、Volatility の期間構造は、ストライクレート(At the moneyかOut of the MoneyかIn the Moneyか)の違いで変わってくるので、イールドカーブの期間構造のように一意に特定できるものではありません。また、At the money が、どのストライクレートになるかも、Cap 期間によって変わるので、これも一意で特定できません。ここでは、(At the Moneyに近いような)なんらかのストライクレートを決め、Cap 価格からBootstrapping によって導出された Caplet の Implied Volatility が導出されたものとして話を進めます。
Cap・Floor 価格から導出されたVolatilityの期間構造を、グラフにして視覚化すると、通常は下記のような形状になる事が多いようです。
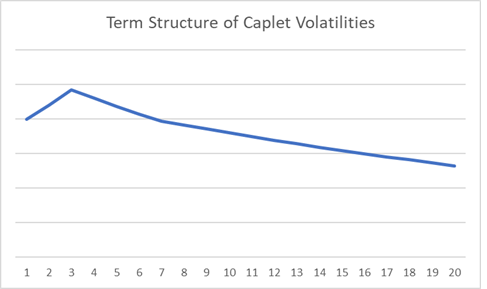
ここで、この (Black) Volatility の期間構造が、なぜ上記グラフのような形状をしているのか考察してみます。その形状は、短期ゾーンから 1~3 年の中期ゾーンに向かって、一旦 Volatility は増加し、そこでピークを付けたのち、長期ゾーンに向かって徐々に低下し、次第になだらかになっています。この形状は、市場環境によって変動しますが、通常の経済環境であれば、ドルやユーロなどの主要通貨で、共通してこのような形になる傾向があります。
通常、イールドカーブの短期ゾーンは、中央銀行の金融政策から影響を大きく受けます。理由は、中央銀行は、資金市場における流動性をコントロールする事で、オーバーナイト金利を中心とした短期金利に影響を与え、それを中央銀行が目標とするレンジに誘導するからです。その際、中央銀行は、その目標レンジを事前に公表し、短期金利がそこから大きくずれないようにコントロールします。さらにここ 20 ~ 30 年で、日米欧の中央銀行は、フォワードガイダンスと言って、金利の目標レンジをいつ頃まで続けるかを公表し、市場に無用のショックを与えないようにしています。これにより、金融市場の参加者は、現在の短期金利の水準が、いつ頃まで続くかについて、ある程度予想がしやすくなりました。その結果、短期ゾーンの金利の Volatility は低めになります。
フォワードガイダンスの期間は、向こう 6 か月から 2 年程度です。それ以降は、経済情勢の変化や、景気に大きなショックを与えるようなイベントが発生すると、金融政策が変更される可能性が出てきます。その結果、金利の不確実性が増し、イールドカーブの 1 年から 3 年のゾーンは、Volatility が高くなる傾向があります。
そこからさらに長期ゾーンに進むにつれ、今度は金利の中心回帰傾向により、Volatility は、低下していきます。Volatility の期間構造のカーブが、1 ~ 3 年の辺りでピークをつけた後、低下していくのは、そういった理由からだと推察されます。
クオンツモデルは、ブラウン運動という、無機的な不確実性を使って表現されるものの、実際に観測される不確実性は、人為的な要因で、かなり影響を受けるという事です。Capの市場価格は、こういった特性を織り込んで、上記のグラフの様な形になると考えられます。市場が、Volatility の期間構造をそのように予想しているのであれば、モデルも、その様子を、出来るだけ表現できた方がいいでしょう。クオンツモデルはそれを受け入れ、それに対応できる柔軟性を持つ必要があります。
さて、ここで注意する点は、Black Model では、 Volatility は現時点からオプション行使日まで一定と仮定しています。一方、LMM の拡散項の Volatility 関数は、t 時における瞬間 Volatility を表しており、これが時間の経過により変化すると仮定しています(関数形が、t の関数になっている)。さらに、LMM はマルチファクターモデルで、各フォワード Libor が相関を持ちながら、複数のブラウン運動により駆動されるので、オプション行使日までの平均 Volatility は、行使日までの Volatility の変化と、相関係数の、両方から影響を受けます。従って、Black Volatility と、LMM の Volatility関数の間には、次のような関係式が成立します。
\[ (BlackVol_{L_i})^2= \frac {1}{T_{i-1}} \int_0^{T_{i-1}} ‖ϕ_i~ψ(t,T_i)~∙ {\bf c_i}‖^2 dt \tag{6.39} \]左辺が、Cap/Floor の市場価格から得られる Black Volatility(の2乗)で、右辺の被積分関数が、LMM の拡散項係数にある Volatility 関数(のノルム)の 2 乗になります。右辺の \(ψ(t)\) を、定数で 1 と置き、相関の情報 \(\bf c_i\) も積分範囲内で一定としててしまえば、LMM の拡散項係数のノルム \(‖ϕ_i∙ \bf c_i ‖\) と Black Volatility は一致します。