上級編 6. Libor Market Model
6.6 モンテカルロシミュレーション
6.6.6 アメリカンタイプのオプションへの対応(続き)
6.6.6.4. Stochastic Mesh Method
6.6.6.4.1 はじめに
Random Tree Method では、オプションの継続保有価値を求める為に、シミュレーションされたひとつのサンプル経路から、さらに分岐するサンプル経路を生成して、シミュレーション内シミュレーションを行うのでした。この方法では、サンプル数が幾何級数的に増大するので、使える商品は限定的で、確率変数の次元数が低次元で、かつオプションの行使日の数が数回の場合にしか対応できませんでした。
Broadie-Glasserman(“Stochastic Mesh Method for Pricing high-dimensional American Options”)は、Random Tree Methodsのその重大な欠点を解消しながら、確率変数が多次元で、期限前行使回数が相当程度あるアメリカンタイプのオプションにも対応できるMCSの方法を提案しました。その方法は、継続保有価値を推定する為に、ひとつのサンプル経路から多くのサンプルを分岐させるのではなく、マルコフ過程を取る i.i.d.(independent and identical distribution 独立同一分布)な他のサンプル経路の情報を使って、継続保有価値を推定するものです。但し、この方法を使うには、ある確率変数の値から、次の行使日の確率変数への遷移確率密度関数が(解析的にあるいは数値的に)求まっている必要があります。Broadie-Glasserman はそのようなテクニックを Stochastic Mesh Method(以下”SMM” ) と名付けています。
6.6.6.4.2 アルゴリズム
まず、そのアルゴリズムを簡単に説明します。
- まず、通常のモンテカルロシミュレーションと同様に、マルコフ過程を取る確率変数のサンプル経路を m 個生成します(マルコフ過程を取る確率変数でなければなりません。従って経路依存型の確率変数を取り扱う場合は原則使えません。)。各サンプルは、通常の MCS と同様、モデルの想定する確率分布に従った、i.i.d.(独立同一分布)なサンプルとして生成されます。離散時間の時間軸には、オプションの期限前行使日と最終行使日を含めます。下のグラフは、そのように生成されたサンプル経路の様子をざっと示したものです。但し、\(T_i,~~i=1,…,M\) はオプションの行使日で、各行使日におけるサンプル値を \(x_i^{(j)},~i=1,…,M,~j=1,…,m\) で示しています。x の上付け文字 (j) はサンプル経路ごとのインデックスを示しています。下のグラフでは、\(T_M\)時における値の高い順に 1,2,…,m とインデックスを付していますが、これはサンプルの生成順ではなく、説明をわかりやすくする為に、一旦生成されたサンプル経路を、値の高いほうから順番に並べ替えたものです。(この図では経路は交差していませんが、当然交差するような経路もあります。)
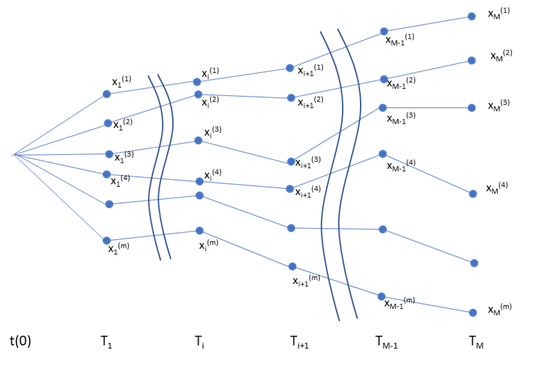
- 次に、各時間軸の確率変数値から、次の時間軸上の各確率変数値への"遷移確率密度関数"を使って、もともと独立であった両者を関連付けます。ここで、\(T_i\) 時における \(x_i^{(j)}\) から \(T_{i+1}\) 時における \(x_{i+1}^{(k)}\) への遷移確率密度関数を、\(f(x_i^{(j)},~x_{i+1}^{(k)})\) と表記します。また、t=0 からみた、各確率変数値(例えば \(x_{i+1}^{(k)}\) の確率密度関数は、\(g(x_{i+1}^{(k)})\) と表記します。この両者は、いずれか一方が特定できれば、もう一方はそこから解析的に求める事ができます。その様子を表したグラフを下記します。但し、見やすさの為に、一部のノードからの線だけ示しています。この繋がりの様子が網目のように見えることから、Stochastic Mesh Method と呼ばれています。
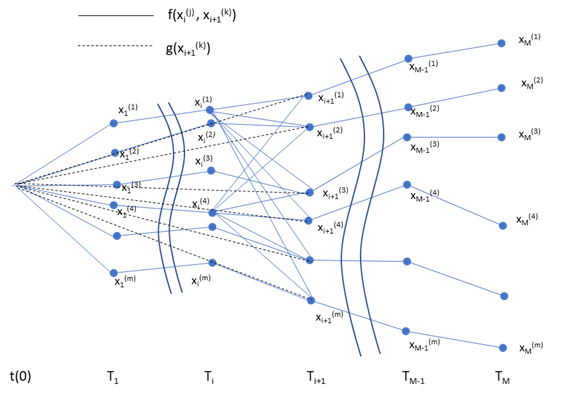
- そして、この2つの確率測度の比を、\(x_i^{(j)}\) からみた、 \(x_{i+1}^{(k)}\) に対応するオプション価値のサンプル平均を取る際のウェイトと看做します。
\[
W_i^{(jk)}=\frac {f(x_i^{(j)},x_{i+1}^{(k)}) }{g(x_{i+1}^{(k)})} \tag{6.138}
\]
このウェイトは、likelihood ratio(尤度比)と呼ばれ、離散的な確率変数の確率測度の測度変換に使われるもので、連続な確率変数におけるラドン・ニコディム微分に相当します。あるいは、\(x_i^{(j)}\) から \(x_{i+1}^{(k)}\)への条件付き確率を求める式と言ってもいいでしょう。このウェイトを使って、\(x_i^{(j)}\) に対応する継続保有価値 \(c_i(x_i^{(j)})\) を、次の行使日 \(T_{i+1}\) におけるオプション価値の加重平均で求めます。オプション価値が簡単に求まるのは、まず最終行使日なので、最初にそれを求め、他の行使日におけるオプション価値は、そこから時間軸を遡及しながら再帰的に求めていきます。
- 具体的には、まず最終行使日におけるオプション価値 \(V_M(x_M)\) を求めます。最終的行使日には継続保有価値がゼロになるので、オプション価値は行使価値 \(h_M(x_M)\) (Payoff関数/ニュメレール)に一致します。この情報と、3.で求めたウェイトの情報を使って、最終行使日の一期手前の \(T_{M-1}\) における各ノード \(x_{M-1}^{(j)},~~j=1,…,m\) における継続保有価値が、下記式で求まります。以下、\(V_i,~c_i,~h_i\) はすべてニュメレールとの相対価格を示します。また、\(V_i(x_i^{(j)}),~c_i(x_i^{(j)})\) は理論値を示し、\(\hat {V}_i(x_i^{(j)}),~\hat{c}_i(x_i^{(j)})\) はシミュレーションされた近似値を示します。
\[
c_{M-1}(x_{M-1}^{(j)}) ≈ \hat{c}_{M-1}(x_{M-1}^{(j)})
=\frac 1 m \sum_{k=1}^m W_{M-1}^{(jk)} \hat{V}_M(x_M^{(k)}).~~~j=1,…,m \tag{6.139}
\]
なぜそうなるかは、後ほど説明します。さらに、この継続保有価値と行使価値とを比べて、\(T_{M-1}\) 時におけるすべてのノードでのオプション価値が求まります。
\[ \begin{align}
\hat{V}_{M-1}(x_{M-1}^{(j)}) & = \max\left[ h_{M-1}(x_{M-1}^{(j)}),~\hat{c}_{M-1}(x_{M-1}^{(j)})\right] \\
& =\max\left[ h_{M-1}(x_{M-1}^{(j)}),~\frac 1 m \sum_{k=1}^m W_{M-1}^{(jk)} \hat{V}_M(x_M^{(k)}) \right],~~j=1,...,m
\tag{6.140}
\end{align}
\]
グラフで示すと下記のようなイメージになります。
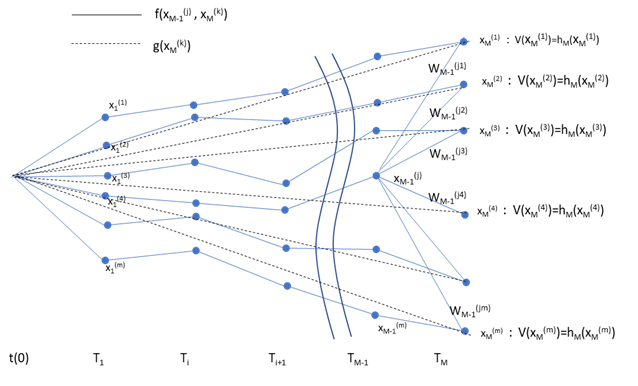
- 上の操作を、時間軸を遡りながら、すべての期限前行使日で行います。すなわち、\(T_{i+1}\) 時のオプション価値がすべてのノードで求まれば、\(T_i\) 時の各ノードにおけるオプション価値は、下記式で求まります。
\[ \begin{align}
\hat{V}_i(x_i^{(j)}) & = \max\left[ h_i(x_i^{(j)}),~\hat{c}_i(x_i^{(j)})\right] \\
& =\max\left[ h_i(x_i^{(j)}),~\frac 1 m \sum_{k=1}^m W_i^{(jk)} \hat{V}_{i+1}(x_{i+1}^{(k)}) \right],~~~j=1,2,...,m
\tag{6.141}
\end{align}
\]
最終的に \(T_1\) 時における、すべてのノード上のオプション価値が求まり、そのサンプル平均を取れば、現時点のオプション価値の近似値が求まります。すなわち、
\[
\hat{V}_0(x_0)= \frac 1 m \sum_{j=1}^m \hat{V}_1 (x_1^{(j)}), \tag{6.142}
\]
既に他のスキームでも説明しましたが、このアルゴリズムでは、価格に上方バイアスがかかります。理由は既に説明した通り(Section6.6.6.2.3)、数学的にはジェンセンの不等式から説明できますが、直観的には、継続保有価値を求めるにあたって、本来なら知る事ができない将来の情報を使っているからです。
6.6.6.4.3 Likelihood Ratio (尤度比)の役割
さて、前のセクションのステップ 4.で説明した、\(T_i\) 時における継続保有価値が、\(T_{i+1}\) 時におけるオプション価値の尤度比加重平均で導出できる点について説明します。それを示した 6.139式を少し修正した式を下記に示します。
\[ c_i(x_i^{(j)}) ≈ \hat{c}_i(x_i^{(j)}) =\frac 1 m \sum_{k=1}^m W_i^{(jk)} \hat{V}_{i+1}(x_{i+1}^{(k)}).~~~j=1,…,m \tag{6.143} \]右辺にあるウェイト \(W_i^{(jk)}\) は、6.138 式で示した通り、\(x_i^{(j)}~から~x_{i+1}^{(k)}\) への遷移確率密度関数 \(f()~と、x_{i+1}^{(k)}\) の確率密度関数 \(g()\) の比で、尤度比(Likelihood Ratio)と呼ばれています。以下に、この式の導出過程を示します。
- まず 継続保有価値 \(c_i(x_i^{(j)})~は、T_i\) 時において確率変数の値が \(x_i^{(j)}\) だった場合の、\(T_{i+1}\) 時のオプション価値の条件付期待値になるのでした。これを式で表すと、以下のようになります。
\[
c_i(x_i^{(j)})=E^{Q_f} \left[V_{i+1}(x_{i+1})~|~x_i^{(j)} \right]=\int f(x_i^{(j)},x_{i+1}) V_{i+1}(x_{i+1})dx_{i+1} \tag{6.144}
\]
但し、\(E^{Q_f} \left[~ ∙ ~|~x_i^{(j)}\right]~は、x_i^{(j)}\) を起点とした遷移確率密度(測度) \(f(x_i^{(j)},x_{i+1})\) による期待値演算。
しかし、右辺の被積分関数にある \(V_{i+1}(x_{i+1})\) は関数形としては求まっておらず、\(Q_g\) 測度下で生成された離散的なサンプル値しか存在しません。また、離散的なサンプル値に対応する遷移確率も求まっていません。(遷移確率密度関数は求まっていても、それは連続な点に対応する確率密度であり、離散的な点への遷移確率ではありません)従って、このままでは、右辺の積分をサンプル平均で近似する事が出来ません。
- そこで、右辺の積分を下記のように変形します。
\[ \begin{align}
\int f(x_i^{(j)},x_{i+1})V_{i+1}(x_{i+1})dx_(i+1)
& =\int \frac{f(x_i^{(j)},x_{i+1})}{g_{i+1}(x_{i+1})}V_{i+1}(x_{i+1})g_{i+1}(x_{i+1})dx_{i+1} \\
& =E^{Q_g} \left[\frac{f(x_i^{(j)},x_{i+1})}{g_{i+1}(x_{i+1})} V_{i+1}(x_{i+1})~|~ x_i^{(j)} \right] \\
& =E^{Q_g} \left[W_i^{(jk)} V_{i+1} (x_{i+1}^{(k)})~|~ x_i^{(j)} \right],
\tag{6.145}
\end{align}
\]
(但し、\(E^{Q_g}[~]\) は、密度関数 \(g(x_i)\) のベースとなる確率測度 \(Q_g\) で計算される条件付き期待値演算)
- すると、この期待値演算は、確率測度 \(Q_g\) で生成されたサンプル値を使って近似値が計算できます。そもそも当初生成されたサンプル \(x_{i+1}^{(j)},~~j=1,…,m\) は、確率密度関数 \(g(~)\) に従う i.i.d.なサンプルとして生成されたものなので、それをそのまま使えばいい訳です。すなわち、 \[ \begin{align} E^{Q_g} \left[ \frac{f(x_i^{(j)},x_{i+1})}{g_{i+1}(x_{i+1})} V_{i+1}(x_{i+1})~|~ x_i^{(j)} \right] & ≈ \frac 1 m \sum_{k=1}^m \frac{f(x_i^{(j)},x_{i+1}^{(k)})}{g_{i+1}(x_{i+1}^{(k)})} \hat{V}_{i+1}(x_{i+1}^{(k)}) \\ & =\frac 1 m \sum_{k=1}^m W_i^{(jk)} \hat{V}_{i+1} (x_{i+1}^{(k)}), \tag{6.146} \end{align} \]
という事で、6.143 式が導出されました。
式をよく見ると、もともと遷移確率密度関数 \(f(~)\) に従う確率測度を使った期待値演算を、当初を生成するのに使った確率密度関数 \(g(~)\) に従う測度に変換して期待値演算を行っている形になっています。尤度比がラドン・ニコディム微分に相当する事が分かります。あるいは、\(W_i^{(jk)}\)を、連続的な繊維確率密度関数を離散的な繊維確率に変換する式と看做せば、上の式は、\(x_i^{(j)}\) からの条件付き期待値を求めていると考える事もできます。
6.6.6.4.4 バイアス
上記のアルゴリズムで近似された現時点のオプション価値は、理論値よりも価格が上になるバイアスがかかっています。すなわち下記不等式が成立しています。
\[ E[V_0(x_0)] ≤ \hat{V}_0(x_0)= \frac 1 m \sum_{j=1}^m \hat{V}_1(x_1^{(j)}) \tag{6.147} \]価格の上方バイアスがかかる理由は、Random Tree Method での理屈と同じです。すなわち、いずれも、継続保有価値の推定を、次のオプション期日におけるオプション価値のサンプル平均で近似する為、本来は知らないはずの将来の情報を基に、オプション行使の判断が行われる為です。 バイアスや、シミュレーションによる誤差は、その他の理由からも発生し、それぞれバイアス・誤差の原因ごとに対応する必要があります。
ここでも、上方バイアスに対する対応方法は、価格に下方バイアスがかかったアルゴリズムでオプション価値を計算し、真の値は、その間にあるだろうという推察できるようにすることです。
下方バイアスのかかったサンプル近似値を導出する方法は、ウェイトを計算する為のサンプルと、実際にオプション価値を計算する為のサンプルを分ける事です。すなわち、最初に、すでに説明したアルゴリズムで、各ノードからのウェイトが求まりますが、それを線形補間などにより、任意の確率変数 \(x_i\) に対応する連続な関数形に変換します。すると、新たにオプション価値の計算用に i.i.d. なサンプル経路を生成しても、各ノード \(x_i^{(j)}\) に対するウェイトがすでに求まっているので、それを使ってオプション価値が計算できます。当初に求めたウェイト関数は、必ずしも最適行使戦略とは限らないので、このようにしてシミュレーションされたオプション価値には下方バイアスがかかります。
当初のアルゴリズムで、上方バイアスのかかった推定値を出し、次のアルゴリズムで下方バイアスのかかった推定値を導出すれば、真のオプション価格は、両者の信頼区間をオーバーラップさせた範囲内に、一定確率で含まれるであろうという推定が可能です。
< 遷移確率密度関数を近似式で求める方法 >
Stochastic Mesh Method を使う条件は、確率変数がガウス分布する場合のように、確率密度関数と遷移確率密度関数が解析的に求まっている必要があります。しかし、仮にそれが解析的に求まらなくとも、数値的に近似値が求まれば、それを使う事も可能です。遷移確率密度関数を数値的に導出する方法は、次のセクションの、最小2乗モンテカルロ法の説明の所で行います。