基礎編 2. 金利の期間構造
2.6 イールドカーブの構築方法(2) Bootstrapping + Interpolation法
2.6.7 データソースにFRAと金利先物を加える
期間が3か月から2~3年までをカバーするデータソースの選択肢として、FRAや金利先物のレート(価格)があります。ここでは、金利先物の価格を使ってBootstrappingを進めてみます。
直近限月の3か月金利先物の最終清算日と価格が下記のようであったとします。
直近限月(最終清算日は、翌月の第3月曜日): 98.62
この限月の対象金利は、翌月の第3月曜日にFixingされ、その2営業日後スタートの3か月物フォワード金利です。 また、価格が示すフォワード金利は、\( 100-98.62=1.38\% \) になります。まずPillarを、先物が対象としている3か月物金利のスタート日とエンド日に設定します。

既にLIBOR金利で \(T_5\) までPillarを設定しましたが、やり直しです。LIBORの所で、\(T_5\) を3か月+2営業日で決めていましたが、それを\(T_6\) に移し、\(T_5\) として金利先物の最終清算日+2営業日を設定し直します。本来なら、最初にデータソースをすべて決めた段階で、Pillarもすべて決めます。

また、今日から翌月の第3月曜日までの日数が38日であったとします。また対象期間となる3か月間の実日数が91日であったとします。すると\(T_5 =38+2=40days,\ T_7=38+2+91=131days\) になります。
キャッシュフローは、LIBOR金利の時と同じく、PV=1 は対象預金のスタート日\(T_5\) が基準になるので、それを今日まで、\(DF(T_5)\) を使ってさらに割引く必要があります。この\(DF(T_5)\) は、\(T_5\) を動かしたので、先ほど計算した\(DF(T_5)\)ではありません。この段階では未知数です。またエンド日\(T_7\) のキャッシュフローは \(1+0.0138×91÷365=1.00344\) になります。方程式を作ると、
\[ \begin{align} \ 0+0+PV_6\times DF(T_5) & -CF_6 (T_7)\times DF(T_7) ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\\ &=0+0+0+0+0+1\times DF(T_5)-0-1.00344\times DF(T_7) \\ &=0 \end{align} \]\(T_0 \) から \(T_4\) のPillarに対応する項は 0 ですが、行列にした時の列に合わせる為に残しています。行列による連立方程式の形で表現すると下記のようになります。前のセクションの連立方程式に対して、3か月LIBORのエンドのPillarを1つ右にずらし、最後の行に金利先物のキャッシュフローを追加しました。
\[ \small{ \left( \begin{array}{rrrrrrrr} 1 & -1.000028 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & -1.000028 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & -1.000194 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & -1.001076 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & -1.00345 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & -1.00344 \\ \end{array} \right) \left( \begin{array}{c} 1\\ DF(T_1)\\ DF(T_2)\\ DF(T_3)\\ DF(T_4)\\ DF(T_5)\\ DF(T_6)\\ DF(T_7)\\ \end{array} \right) = \left( \begin{array}{c} 0\\ 0\\ 0\\ 0\\ 0\\ 0\\ 0\\ 0\\ \end{array} \right) } \]見ての通り、未知数が7個あるのに対し、式が6個しか無く、このままでは解けません。ここで、\(DF(T_i)\) にInterpolationを使います。Interpolationの方法は様々ですが、ここでは簡単で、実務でも比較的よく使われる、\(DF(T_i)\) の対数を 線形補間する方法を使ってみます(Log-linear on Discount Factor)。この方法は、Zero Coupon Rateを期間加重した値を直線で結んでいるのと同じです。(∵\( \ln DF(T_i) = − r(T_i)\times T_i\) なので)
\(DF(T_4)\) と \(DF(T_6)\) は既に求まっているので、\(DF(T_5)\) は次の方程式を解けば求まります。
\[ \ln DF(T_5)=\ln DF(T_4)+(\ln DF(T_6)-\ln DF(T_4))\times \frac{(T_5-T_4)}{(T_6-T_4 )} \]これを解くと、\(DF(T_5)=0.9986\) となりました。これで未知数は\(DF(T_7)\) だけになったので、連立方程式の解が求まり、\(DF(T_7)=0.99517\) となりました。
\(DF(T_i)\) の配列が求まれば、Zero Coupon Rate とForward Rateも求まります。
FRA(Forward Rate Agreement)をデータソースとして使う場合も、日数計算方法など細部で異なる点はありますが、アルゴリズムとしては同じ手順です。
金利先物をデータソースとして使う場合、実はConvexity Adjustmentの調整が必要です。上の例では、それを行わずに原データをそのまま使いました。
<Convexity Adjustment >
金利先物をデータソースとして使う場合、いくつか注意点があります。ひとつは、先ほどCash Flow額を計算する際の日数計算方法は 実日数÷365(Actual/365)を使いました。先物の対象金利がLIBORなのに、Actual/360を使わなかったのは、取引所が決めた先物の清算価格の計算方法では、3か月を0.25年とみなしているからです。LIBOR金利の1bpと、金利先物の1bpでは、実際の値が微妙に異なるという事です。
さらに、金利先物については、Convexity Adjustmentが必要になります。 金利先物の価格変化(すなわち金利の変化)に対する損益変化は、価格1bpあたり0.25bpの直線になります。さらに先物の清算は毎日行われ、価格変動にあわせて変動証拠金(Variation Margin)が、通常、翌営業日に授受されます。これに対し、FRAでフォワード金利をヘッジした場合、清算はフォワード金利のスタート日に行われる為、大分先になります。その結果、金利変動による損益インパクトは、清算日からディスカウントされるので、インパクトが若干和らぎます。金利の上下に対する損益インパクトをグラフにすると
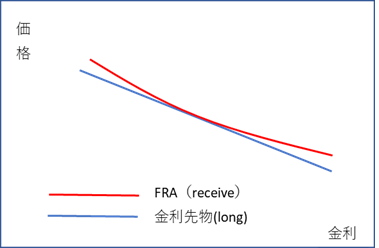
FRAの損益カーブは左下に凸になっており、このカーブの度合いをConvexityと呼びます。一方、金利先物の損益カーブは直線になります。そうすると、グラフから判る通り、金利先物を買った人(金利で言えば、金利低下に賭けた人)は、FRAでフォワード金利をヘッジした人よりも、不利になります(FRAでの利益>金利先物での利益)。 金利先物を売った人は、逆に有利になります。そのインパクトは、オプションと同じ様に、金利のVolatilityに依存するので、何等かの金利オプションモデルを使って計算する必要があります。その調整値をConvexity Adjustmentと呼びます。
そのインパクトは、今のような低金利環境では、限月の近いものでは僅かであり、無視していいかもしれません。しかし長い限月の金利先物では、金利が高いほど、無視できない大きさになります。
実は、FRAについても、僅かながら似たような修正が必要かも知れません。FRAの一般的な取引慣行では、FRAで合意した基準レートと、実際にFixingされたLIBORレートの差額決済は、そのLIBOR期間のスタート時に行われます。実際のLIBOR金利の支払いはLIBOR期間のエンド日に行われるので、差額決済分の再投資・再調達にかかる微妙な修正が必要になります。今のような低金利時代であれば、非常にわずかな調整なので無視していいかも知れません。
ここでは、具体的なConvexity Adjustmentの方法までは説明しませんが、そういう調整が必要だという事だけ紹介しました。