2.Implementing QuantLibの和訳
Chapter-II. Financial Instruments and Pricing Engines
2.2 Pricing Engines 価格計算アルゴリズムのオブジェクトモデル
このChapterの冒頭で申し上げた、Model Libraryに要求される2つの要請の内、2つ目について説明します。ある具体的な金融商品について、価格計算の方法は、1つとは限らない事、さらにユーザーは様々な理由で複数の計算方法を使う場合がある、という事です。ひとつ典型的な例として、 株のヨーロピアンオプションで考えてみましょう。ある人は、Black-Scholesの公式を使って、オプションの市場価格からImplied Volatility(オプション価格に内包されているVolatility)を計算したいと考えます。あるいは、そこから、Stochastic Volatility Modelのカリブレーション(パラメータの調整)を行って、より複雑なオプションの価格計算に使ったりします。さらに、Black-Scholesの公式とFinite-difference scheme(有限差分法)を使ったアルゴリズムの計算結果を比べて、有限差分モデルの検証に使ったりします。さらには、モンテカルロシミュレーション法による複雑なオプション価格の計算において、ヨーロピアンオプションの解析解を、control variate(訳注:モンテカルロシミュレーションによる解の収束速度をアップさせる為の制御変量)として使ったりします。
従って、ひとつの金融商品について、複数の方法で価格計算ができるような仕組みにしたい訳です。その場合、当然ながらperfromCalculations( )メソッドを複数個実装するという方法は、望ましくありません。なぜなら、そうする為には、ひとつの金融商品について、複数のクラスを作らなければならなくなるからです。(訳注:Template Method Patternを使っているので、performCalculations( )メソッドは、派生クラス毎に、ひとつだけ実装する事を想定している為。) そうする為には例えば、EuropeanOptionクラスから、AnalyticEuropeanOptionクラスとMcEuropeanOptionクラスを派生させる事になりますが、この方法だと、2つの点で問題があります。まず概念的に考えて、ひとつの商品の為にふたつの箱を用意するようなものです。Gertrude Steinの言い回しを使えば、「ヨーロピアンオプションがヨーロピアンオプションであると言っているのは、ヨーロピアンオプションはヨーロピアンオプションであるという意味である。」という事です(訳注:Steinのオリジナルの表現は、“Rose is a Rose is a Rose is a Rose.”) また、使用上の問題として、run-time(プログラム実行時)に価格計算方法の変更ができないという点です。
この問題の解決方法は、Strategy Patternを使う事です。すなわち、その商品のオブジェクトに、価格計算方法をカプセル化した他のオブジェクトを持たせる事です。そのようなオブジェクトをPricing Engineと呼ぶことにします。ある特定の商品オブジェクトが、その商品に対応したPricing Engineを選択できるようにし、その選択したPricing Engineに、計算に必要な引数を渡し、そのEngineが価格計算を行い、そのEngineから計算結果を返させるような仕組みが想定されます。そうすると、InstrumentオブジェクトのインターフェースであるperformCalculations( )の実装は、おおむね下記のようなプログラムコードになると推察されます。
void SomeInstrument::performCalculations() const {
NPV_ = engine_->calculate(arg1, arg2, ... , argN);
} ここでは、(performCalculations( )の中で呼び出される)Pricing Engineのcalculate( )メソッドを、ベースクラスで仮想関数としてインターフェースを定義し、具体的な計算方法は、派生クラスとなるPricing Engineで実装する事が想定されます。
残念ながら、この方法によるアプローチは、想定通りに機能しません。問題は、calculate( )を呼び出すプログラムコード(訳注:performCalculations( )の実装部分)を、ベースクラスの中で1回の実装で済ませたいのに、それが出来ないという事です。なぜならベースクラスは、個別の商品毎に必要な、Pricing Engineの引数を知る余地がありません。それらはInstrumentの派生クラス毎に、数も型も千差万別です。同じ事は、Pricing Engineが返す計算結果についても言えます。例えば、金利スワップであれば、固定金利と変動金利スプレッドのFair Value(市場レートにフィットした固定金利の水準)を計算して返す事が想定されますが、一般的なヨーロピアンオプションでは、価格以外に様々なGreeks(訳注:ギリシャ文字、転じて様々なリスク感応度のこと。)を返す事も想定されます。
上記のサンプルコードように、Pricing Engineに渡す引数を明示して列挙するようなインターフェースは、望ましくない結果をもたらします。異なる金融商品に対応する、異なるPricing Engineは、当然ながら異なったインターフェースを持つはずであり、それを一本のベースクラスで表現する事はできません。そうすると、InstrumentからPricing Engineのcalculate()を呼び出すメソッドは、Instrumentの派生クラス毎に作り直さなければならなくなります。そこに大変な困難が存在します。
我々が選択した解決策は、Pricing Engineの引数や返値を、arguments とresultsという柔軟な構造体でやりとりする方法でした。この2つの構造体を派生させて、個別の金融商品(のPricing Engine)ごとに必要な“引数”と“返し値”の構造体を作り、Pricing Engineオブジェクトに保持させます。またInstrument(の派生クラスの)オブジェクトは、Pricing Engineの持つ引数と返し値の情報を、書き込んだり読み込んだりできるようにします。
Listing 2.5に、このような構造を組みこんだPricing Engineクラスの定義と、その内部クラスとして定義されたargumentsクラスと resultsクラス、さらに、補助的役割を持つGenericEngineクラス・テンプレートのコードを示します。この最後のクラスは、Pricing Engineのインターフェースの大半を実装しており、QuantLibを利用したい開発者は、個別のPricing Engineのcalculate( )メソッドのみを実装すれば良いだけです。argumentsとresultsクラスには、使いやすいように(入力データの)ドロップBoxを使えるメソッドが備え付けられています。すなわちarguments::validate( )メソッドは、入力データとして受け取った引数が、有効なデータ範囲の中に納まっているかどうかチェックする機能をもっています。また、results::reset( )メソッドは、Pricing Engineが価格計算を開始する前に、前回計算した結果を消去します。
Listing 2.5: Interface of PricingEngine and of related classes.
class PricingEngine : public Observable {
public:
class arguments;
class results;
virtual ~PricingEngine() {}
virtual arguments* getArguments() const = 0;
virtual const results* getResults() const = 0;
virtual void reset() const = 0;
virtual void calculate() const = 0;
};
class PricingEngine::arguments {
public:
virtual ~arguments() {}
virtual void validate() const = 0;
};
class PricingEngine::results {
public:
virtual ~results() {}
virtual void reset() = 0;
};
// ArgumentsType must inherit from arguments;
// ResultType from results.
template <class ArgumentsType, class ResultsType>
class GenericEngine : public PricingEngine {
public:
PricingEngine::arguments* getArguments() const {
return &arguments_;
}
const PricingEngine::results* getResults() const {
return &results_;
}
void reset() const { results_.reset(); }
protected:
mutable ArgumentsType arguments_;
mutable ResultsType results_;
}; この考え方をベースに作られた新しいクラスを使って、汎用的なperformCalculations( )の実装例を示すことができます。すでに述べたStrategy パターンに加え、ここではTemplate Methodパターンも使って、Instrumentの派生クラスで足りない機能を書き加えられるようにしています。そのプログラムコードをListing 2.6に示します。インナークラスのInstrument::resultsクラスが定義されている所に注意して下さい。このクラスは、Pricing Engine::resultsクラスから派生しており、個別のInstrument用の計算結果を保持します。(Instrument;;resultsクラスは、std;;mapオブジェクトをメンバー変数として保持しており、そこに追加の計算結果を保持できるようになっています。但し、それを記述したコードは下記では省略されています。)
Listing 2.6: Excerpt of the Instrument class.
class Instrument : public LazyObject {
public:
class results;
virtual void performCalculations() const {
QL_REQUIRE(engine_, "null pricing engine");
engine_->reset();
setupArguments(engine_->getArguments());
engine_->getArguments()->validate();
engine_->calculate();
fetchResults(engine_->getResults());
}
virtual void setupArguments(
PricingEngine::arguments*) const {
QL_FAIL("setupArguments() not implemented");
}
virtual void fetchResults(
const PricingEngine::results* r) const {
const Instrument::results* results =
dynamic_cast<const Value*>(r);
QL_ENSURE(results != 0, "no results returned");
NPV_ = results->value;
errorEstimate_ = results->errorEstimate;
}
template <class T> T result(const string& tag) const;
protected:
boost::shared_ptr<PricingEngine> engine_;
};
class Instrument::results
: public virtual PricingEngine::results {
public:
Value() { reset(); }
void reset() {
value = errorEstimate = Null<Real>();
}
Real value;
Real errorEstimate;
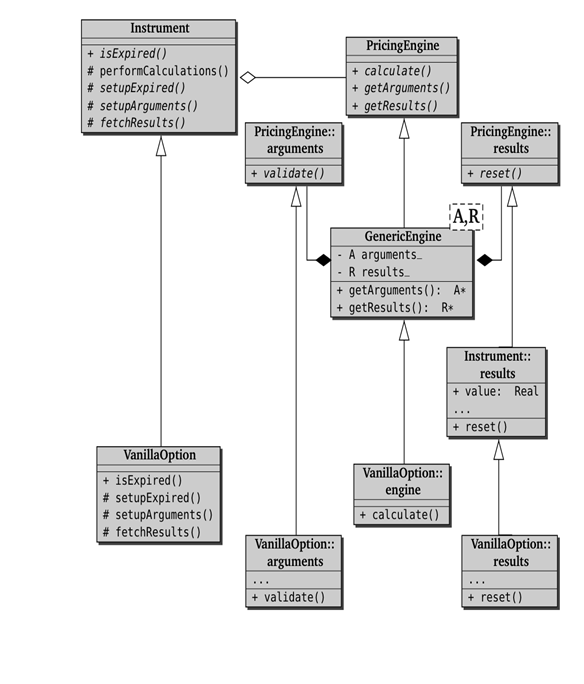
}; performCalculations( )メソッドの実際の動作は、それを補助する複数のクラス(すなわち、Instrument, Pricing Engine、arguments およびresultsの各クラス)に作業分担されています。そのような補助の動作(次の段落で説明)を理解するには、下記のFigure 2.2:UMLシーケンス図(Unified Model Language Sequence)をよく見て下さい。さらに、各クラス間の静的な関係はFigure 2.3を参照下さい。
Figure 2.2: Sequence diagram of the interplay between instruments and pricing engines
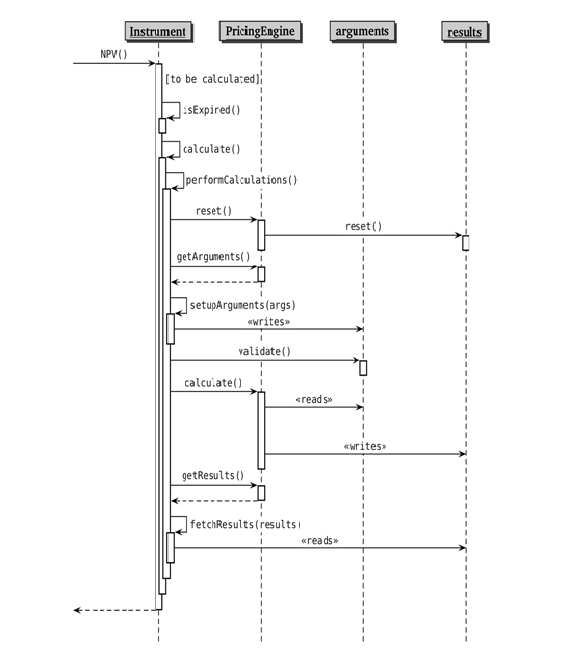
Figure 2.3: Class diagram of Instrument, PricingEngine, and related classes
InstrumentクラスのNPV( )メソッドを呼び出すと(もしその商品が満期を迎えていなくて、価格やリスク量を計算する必要がある状態にあるのなら)、そこからさらにperformCalculations( )を呼び出します。そこからInstrumentオブジェクトとPricing Engineとの間の連携が始まります。まず最初に、Instrumentは、Pricing Engineそのものが存在しているかどうかチェックし、もしそうでないなら計算をそこでストップします。もしPricing Engineが見つかったなら、Instrumentは、Pricing Engineに対し、データのリセットを指令します。その指令は、reset( )メソッドを使って、そのInstrument固有のresults構造体に伝達され、その構造体の中の古いデータを消去し、新しい計算結果を保持できる状態にします。
ここで、Template Methodパターンが登場します。Instrumentオブジェクトは、Pricing Engineオブジェクトに対し、arguments構造体を渡すよう要求し、Pricing Engineは、その構造体のポインターを返します。そのポインターはInstrumentのsetupArguments( )メソッドに渡されますが、このメソッドがTemplate Methodパターンにおける可変部分の役割を果たします。このメソッドは、まず渡された引数(arguments構造体)がその商品に適合するものかどうかチェックし、もしそうなら、そのarguments構造体に、自分のメンバー変数を代入していきます。最後に、arguments構造体は、入力されたデータが有効範囲内のものかどうかをvalidate( )メソッドを使って行います。
この段階で、Strategy Patternの用意ができました。引数が準備できたので、Pricing Engineオブジェクトは、その商品の価格計算を、(そのPricing Engine独自のアルゴリズムを実装した)calculate( )メソッドを使って実行するよう要求されます。Pricing Engineは、argumentsから受け取った入力データを使って計算を実行し、計算結果をresults構造体へ書き込みます。
Pricing Engineが以上の動作を完了した後、実行手順はInstrumentオブジェクトに戻り、Template Methodパターンが引き続き読み解かれます。すなわちfetchResults( )メソッドが呼び出され、Pricing Engineに対しresults構造体を渡すよう要求し、そのオブジェクトがDowncastされ、そのメンバー変数へのアクセスを可能にし、その内容を自らのメンバー変数にコピーします。Instrumentベースクラスは、すべての商品に共通のresults構造体をデフォールトで定義しており、各派生クラスで、さらに追加の計算結果を保有するよう拡張できます。
< 純粋でない仮想関数 >
Listing 2.6を見て、setupArguments( )メソッドが、純粋仮想関数として宣言されず、例外処理を行うよう実装されているのを、不思議に思われるかもしれません。(訳注:setupArguments( )は実装されていませんというエラー処理しか行わないメソッドを作る意味があるのか、純粋仮想関数にして、派生クラスで実質な内容を実装すればいいのではないか、という疑問) その理由は、開発者が、派生クラスにおいてperformCalculations( )をOverrideして実装するだけの場合は、意味のないメソッドをその派生クラスの為に実装するのを強制しないようにするためです。
<ライセンス表示>
QuantLibのソースコードを使う場合は、ライセンス表示とDisclaimerの表示が義務付けられているので、添付します。 ライセンス