実務で使える金融工学　上級編

上級編　１．　イールドカーブ

1.1 Interpolation

1.1.2 Linear Interpolation （線形補間）

1.1.2.1 Discount Factorの対数の線形補間（Linear on Log of Discount Factor）

Pillar間を一次式で補間したものをLinear Interpolationと呼びます。補間される値を何にするかについては、すでに述べた通り、Par RateやDiscount Factorを補間する方法は、欠点が多く、実務ではあまり使われていません。さらにZero Rateをそのまま線形補間する方法も、あまり一般的ではないと思います。従って、これらの解説は省略したいと思います。 

線形補間法で、よく紹介されている方法として、各Pillarにおける“Discount Factorの対数”を取って、それを線形補間する方法があります。２点のPillarでのDiscount Factorが判れば、次の式を使ってDiscount Factorを線形補間できます。 

\[ \ln DF(t)=\ln DF_{i+1} \frac{t-t_i}{t_{i+1}-t_i}+\ln DF_i \frac{t_{i+1}-t}{t_{i+1}-t_i} \tag{1.1.1} \] \[ =-r_{i+1} t_{i+1} \frac{t-t_i}{t_{i+1}-t_i}- r_i t_i \frac{t_{i+1}-t}{t_{i+1}-t_i} \tag{1.1.2} \]

但し 

\[ DF_i,\ DF_{i+1} ∶\ Discount\ Factor\ on\ t_i\ and\ t_{i+1},\ \ t_i\lt t\lt t_{i+1} \] \[ r_i,\ r_{i+1} ∶\ Zero Rate\ on\ t_i\ and\ t_{i+1},\ \ t_i\lt t \lt t_{i+1} \]

Discount Factorの対数が補間できれば、その指数を取ればDiscount Factorそのものが導出でき、さらにそこからZero RateとPillar間の区間フォワード金利も導出できます。Discount Factorの対数は　\( \ln DF(t)=\ln e^{-r(t)t} =-r(t)t　\) なので、この方法は、各PillarにおけるZero Rateに期間を掛けた値を線形補間しているともいえます（1.1.2式）。 

この方法を使うと、Pillar間の瞬間フォワード金利が一定になり、区間フォワード金利と一致する事になります。その為、この方法はPiecewise Constant Forward法とも呼ばれています。区間毎の瞬間フォワード金利が一定の為、Pillarを跨ぐと瞬間フォワード金利がジャンプします。この方法による瞬間フォワード金利のカーブは、階段関数のような形状になります。 

"1.1.2.2 Linear on Log of Zero Rate （ゼロクーポンレートの対数を線形補間）

２つのPillarにおけるZero Coupon Rateの対数を線形補間する方法で、対数を取ることによって、Zero Coupon Rateがカーブの右方向に行くほど緩やかになる傾向を表現できます。関数形で表現すると、 

\[ \ln r(t)=\ln⁡r_{i+1} \frac{t-t_i}{t_{i+1}-t_i}+\ln⁡r_i \frac{t_{i+1}-t}{t_{i+1}-t_i}\ \ \tag{1.1.3} \]

但し、\(r_i,\ r_{i+1}∶\ Zero\ Rate\ on\ t_i\ and\ t_{i+1},\ \ t_i\lt t\lt t_{i+1}\) 

この式から瞬間フォワード金利を導出すると 

\[ f(t)=r(t)\left( \frac{t}{t_{i+1}-t_i} \ln \frac{r_{i+1}}{r_i}+1\right)\ \tag{1.1.4} \]

となります。この式から、　\( r_i \gg r_{i+1} \) の場合、たとえ　\( r_i \gt 0,\ r_{i+1} \gt 0 \) であっても、瞬間フォワード金利が\( t_{i+1}\) 近くでマイナスになります。 

1.1.2.3 Piecewise Linear Continuous (Instantaneous) Forward
     (瞬間フォワード金利の連続な線形補間)

上記の2方法は、いずれも瞬間フォワード金利のカーブがPillarにおいてジャンプし非連続となります。瞬間フォワード金利のカーブは、瞬間短期金利の将来の変化を予想していると見做せるので、それがPillarに到達する度にジャンプするのは、経済現象としていかにも不自然です。 

瞬間短期金利が非連続となるのが、問題であるのなら、それが連続になるように線形補間するとどうなるでしょうか？　結論から言えば、もっと問題が大きくなり、とても使えないカーブになります。 

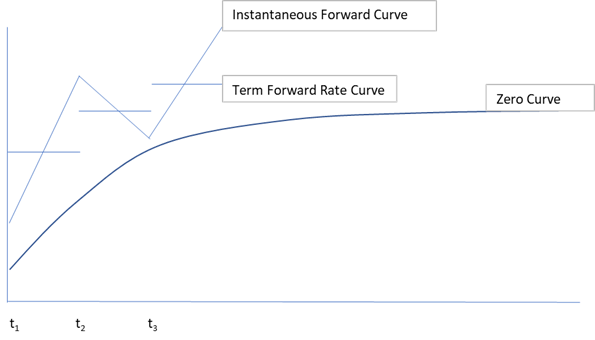
この方法は、各Pillarにおける瞬間フォワード金利を線形補間する方法と考えられますが、そもそも各Pillarにおける瞬間フォワード金利は一意に決まりません。Pillar間の区間フォワード金利は一意に決まりますが、その区間の瞬間フォワード金利は、その平均が区間フォワード金利と一致しさえすればよく、区間の両端の瞬間フォワード金利は任意に決められます。このInterpolation法では、左端のPillarの瞬間フォワード金利を無理やり何等かの値に設定すると、そこから、区間フォワード金利の中点を通る直線上に、次のPillarの瞬間フォワード金利が決まります。そこから、次の区間の区間フォワード金利の中点を通る直線を引き、その延長線上に、次のPillarにおける瞬間フォワード金利が決まります。そうすると、瞬間フォワード金利のカーブは、区間フォワード金利の中点を通る、ジグザグの直線になります。グラフで見ると明白です。瞬間フォワード金利が非連続なのは、不自然ですが、連続にしても、この形状はやはり不自然です。