基礎編 5. リスク量の計測
5.2 Sensitivities(感応度)の計測
5.2.3 非線形リスク つづき
5.2.3.3 やっかいな非線形リスク
前のセクションで説明した通り、シンプルなオプションであれば、ガンマリスクはそれ程気にする必要はなく、ベガリスクをコントロールしておけば、ガンマリスクも概ねコントロールされると言いました。
ところが、デジタルオプションや一部のバリアオプションでは、とんでも無いガンマリスクが発生する可能性があり、ベガのコントロールだけでは到底コントロールできない恐れがあります。これらのオプションのPayoff関数は、バリアをヒットするとジャンプします。Payoff関数が、バリアにおいて微分不可能で、かつ非連続になっているという事です。日本で、比較的ポピュラーであった日経リンク債に内在しているオプションは、ノックイン型のプットオプションですが、その典型的なものです。
その辺の様子を視覚的に理解する為に、日経リンク債に内包しているオプションの価格をグラフで示します。このグラフは、プットオプションを提供している証券会社側(オプションの買い手)からみたもので、インデックスが下落すると価格が上昇する様子を示しています。グラフは、オプション満期日までが、3カ月、1カ月、1日の3パターンと、比較のために、シンプルなヨーロピアンプットの価格も示しています。
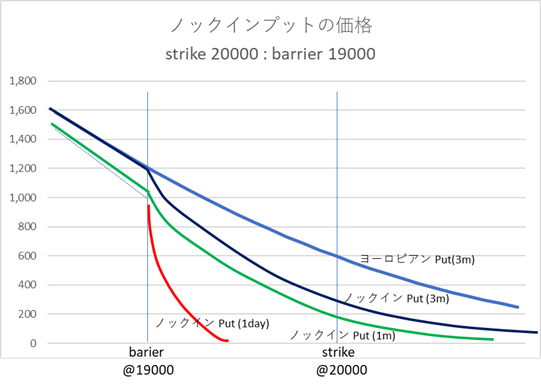
バリアの19000から左上の伸びている直線が、Payoffになります。ストライクは20000ですが、バリアにヒットするまでは行使ができず、Payoffはゼロです。ところがバリアをヒットした途端に1000ポイントIn the Moneyのプットオプションが実現し、Payoffがジャンプします。
ノックインオプションの価格を見ると、インデックスが下落しバリアに接近するにつれ、価格が急上昇します。オプションのデルタは、この価格曲線の傾きですが、グラフを見て判る通り、バリアに近づくにつれて傾きがかなりきつくなっていきます。この傾きは、右下下がりで45度の時、マイナス1(−100%)となり、対象資産の価格変化率とプットの価格変化率が同じになります。通常のヨーロピアンプットであれば、デルタはDeep in the Moneyになるに従い−100%に近づきますが、決して−100%を超える事はありません。しかし、ノックインプットの場合は、傾きはマイナス1より急こう配になり、オプション期日に近づき、かつバリアに近づくにつれ−∞に発散していきます。そして、バリアをヒットした瞬間、デルタは約−100%に戻ります。
その様子をグラフにしたものを示します。

デルタは確率変数による1階微分なので、このデルタ曲線の傾きが2階微分すなわちガンマに相当します。ガンマはデルタと共に、バリアに近づくにつれて傾きが急になっています。すなわちガンマがどんどん大きくなります。この時のガンマはオプションの買い手にとってはポジティブガンマです。
特異点を跨ぐと、すなわちバリアをヒットすると、巨額のマイナスのガンマ(negative gammaあるいはガンマショートとも言います)が発生します。すなわち、それまで行ってきたデルタヘッジを一気処分する必要があります。オプショントレーダーは、このガンマショートを非常に嫌います。
このタイプのオプションでは、オプション期日直前に対象資産の価格がバリアの直前に位置する場合、バリアをヒットするか否かで、損益は天地ほどの差がつきます。ヒットすれば、巨額のプレミアムが手に入りますが、ヒットしなければオプションはExpireし、価値がゼロになります。すなわち、オプションの時間価値が、通常のオプションと比べて極端に大きくなります。先ほど、オプションの時間価値(シータ)とガンマリスクが均衡すると述べましたが、この極端に大きくなった時間価値の対価として、非常に大きなガンマリスクが発生することになります。さすがにこのガンマリスクは放置できません。ところがヘッジしたくても、ヘッジもままならないのです。
このリスクは、ベガのヘッジでは対応しきれません。ベガはオプションの残存期間が小さくなるにつれ0に収束していくので、オプション期日直前では非常に小さな値になっています。それをヘッジしても殆ど意味がないからです。デルタヘッジを理論通りに行う事もできません。無限大とは言わなくても、バリア直前でデルタが巨額になり、しかも、価格が少し動くだけで激しく変化するので、理論通りのヘッジは実務上不可能です。しかし、実際に、日経リンク債にからむオプションは大量に取引されてきました。実務では、このリスクにどう対応していたのでしょうか。
5.2.3.4 やっかいな非線形リスクのコントロール
実際の所、対応方法は、証券会社やトレーダーによってまちまちであったと思います。
放置するのもひとつの手です。対象資産の価格がバリアに近づくと、オプション価格は急激に変動しますが、デルタヘッジを理論通りに行わず、市場の動きに対し為すがままにし、損益変動を甘んじて受け入れるというものです。バリアをヒットしなくても、損益の振れの最大幅は、デジタルオプションのプレミアムの範囲内なので、下手に巨額のデルタヘッジをする方が、損失が大きくなるかもしれません。
もう少しスマートに見えるリスク管理方法は、Strike Shiftと呼ばれる手法で、バリアの水準を、契約で取り決めた水準よりも離れた所にあると見做してヘッジ比率を決め、デルタヘッジを行うというものです。バリアの水準を遠くにする事によって、オプションの価値を低く保守的に評価し、デルタやガンマがあまり大きくならない領域でデルタヘッジを行うものです。仮に、契約上のバリアをヒットした場合、幸運にも予定外の収益が発生したとして喜んでそれ頂くという事になります。但し、この方法は、オプションを、本来の契約と異なる条件で評価する事になるので、会計上や税務上、その保守的な価格評価が認められない可能性があります。あくまでトレーディングデスクのポジションリスク管理として行うもので、会計上・税務上の損益と、トレーディングデスクが認識する損益の誤差は、トレーディングデスクが甘んじて受け入れる事になります。
あるいは、市場価格がバリアから遠い時に、バリア近辺のStrike Spreadのポジションを事前に仕込んでおく方法もあります。バリアと同じストライクのオプションをバリアオプションの元本より大きめに売り、少し離れたストライクのオプションを買ってストライクスプレッドから発生するロスを確定させておきます。但しその額は、バリアヒットで得られる利益の範囲内にします。市場価格がバリアに近づくと、バリアオプションのガンマが急激に大きくなりますが、事前に仕込んだオプションのガンマショートである程度は相殺されます。シンプルなオプションから発生するガンマは、バリアオプションのガンマより、Strike近辺ではどうしても小さくなり、完全なガンマヘッジにはなりませんが、デルタヘッジの負担を少しでも緩和できます。
いずれも、不完全な方法で、かつコストもかかりますが、若干でもリスクを軽減できます。という事は、トレーダーは、こういったコストも勘案して取引き価格を決めるはずです。Fundamental Theory of Asset Pricingの前提が崩れているので、オプションモデルでの理論価格では、もはや取引きできないという事です。
5.2.3.5 さらにやっかいな非線形リスク
確率変数が複数のオプションモデル(Multi-Factor Model)を使う場合は、すなわち、オプションの対象資産の価格を動かすリスクファクターが複数存在する場合は、話はさらに複雑になります。
仮に、あるオプション価格C(・)が、2つの確率変数X(t)とY(t)に依存して決まるとします。また、この2つの確率変数は、相関係数ρを持つ2つのブラウン運動Wx、Wyに従う、次の様な確率過程を取ると仮定します。
\[ dX(t)=\alpha X(t)dt+\sigma_X X(t) dW_X (t)\\ dY(t)=\beta Y(t)dt+\sigma_Y Y(t) dW_Y (t)\\ dW_X (t) dW_Y (t)=\rho dt \]伊藤のレンマを使ってオプション価格の確率過程の式は、下記のように導出されます。
\[ dC(t,X(t),Y(t))=\frac{\partial C( )}{\partial t}dt+\frac{\partial C( )}{\partial X(t)} dX(t)+\frac{\partial C( )}{\partial Y(t)} dY(t) \hspace{80mm}\\ +\frac{1}{2}\sigma_X^2 X(t)^2 \frac{\partial^2 C( )}{\partial X(t)^2} dt +\frac{1}{2}\sigma_Y^2 Y(t)^2 \frac{\partial^2 C( )}{\partial Y(t)^2} dt +\frac{1}{2} \rho \sigma_X \sigma_Y X(t) Y(t) \frac{\partial^2 C( )}{\partial X(t)\partial Y(t)} dt \]この式にある通り、第4項、第5項、第6項は、2階微分の項になり、オプション価格のSensitivitiesは、非線形のリスクまで勘案する必要がある事を示しています。第4項は、Xに対するガンマ、第5項はYに対するガンマ、第6項は、XとYに対するCross Gammaと呼ばれています。このCross Gammaは、第6項の係数を見れば判る通り、相関係数ρ の影響を受けます。このρ が非常にやっかいです。
価格計算を行う場合、このρ の値を、何等かの仮定をおいて一定に決めます。しかし、実際に観測される市場リスクファクター間の相関係数は、極めて不安定です。場合によっては、観測期間によって正負が逆転する事さえあります。また、ρ を対象とした金融商品は(私の知る限り)存在しないので、ヘッジもできません。同じX とY と相関係数の影響を受ける、別のオプションで反対売買をする方法もありますが、通常こういった商品は流動性が低く、ヘッジコストがかかりすぎる問題があります。
こういったオプションでデルタヘッジ戦略を取った場合、仮にスムーズにデルタヘッジが出来て、X とY の実現Volatilityが予想Volatilityと一致したとしても、実現した相関係数がモデルの相関係数と異なった場合は、ネット損益はゼロに収まりません。そして、その相関は、予想が難しく、不安定で、ヘッジもできないのです。ここでもFundamental Theory of Asset Pricingの大前提が崩れています。
このリスクを、トレーダーはどのようにコントロールしているのでしょうか。少なくとも、私のいたある会社のトレーダーは、一切コントロールせず、リスクをそのまま受け入れていました。別の会社では、一定のリザーブ(引当金)を積んで、相関係数がモデルの想定外の動きをして発生する損失の備えをしていました。いずれにしても、私の知る限り有効なコントロール方法は無いという事です。