上級編 1. イールドカーブ
1.1 Interpolation
1.1.1 Interpolation法の種類と特徴
Bootstrapping法では、Par CurveからPillar時点に対応するZero RateやDiscount Factorは特定できますが、Pillar間の値については、何等かのInterpolator(補間関数)を使って推定するしかありません。どのようなInterpolation法を使っても、あくまで推定なので、どの方法が正しく、どれが間違っているという議論にはなりません。しかし、価格計算で使われるイールドカーブの場合、それを使ってベンチマーク商品の価格計算をした場合、必ず市場価格と一致しなければなりません。デリバティブズ評価に使うイールドカーブ構築では、それが絶対条件です。
Interpolation法で、絶対的な方法が無いのであれば、様々な方法からどのような基準でInterpolationの方法を選択すればよいのでしょうか? カーブの形状が滑らかで、それらしく見えれば十分かと言うと、そういう訳でもありません。Hagan-Westの論文では、Interpolation法を選択する際に、望ましい性質として次の様な点をあげています。
- Forward Curveの形状が自然か? Forward Rateは通常、1カ月や3カ月のForward Libor形状が大事だが、実質的には、瞬間Forward Curveの形状を見れば良い。 瞬間Forward Curveについては、“連続性”と“マイナス金利にならない事”が大事。(注:マイナス金利自体は、それが当たり前になっている今では問題になりません。しかし、区間フォワード金利がすべての区間でプラスの領域にあるにも関わらず、瞬間フォワード金利が、一部の区間でマイナスになるようであれば問題があります。Interpolationの方法によっては、そういう事が起こり得
- Interpolation法のLocality(局所性)。原データのレートが動いた時に、その影響が、局所的に留まるか、カーブ全体に影響を及ぼすのか?
- Forward Curveが、連続であるだけでなく、安定的か? 原データのレートの微小な変化が、Forward Rateに対し、最大でどの程度影響を与えるのか? あるPillarのZero Rateを少しだけ動かすと、その前後のForward Rateが、増幅されて変化し、さらに波になってカーブの後ろの方に波及していきます。それ自体は止むを得ませんが、その程度を把握しておく必要があります。単純なInterpolation法であれば、影響度を正確に計算できますが、複雑な方法では、推定値を求める必要があります。
- ヘッジ商品の価格変化が与える影響のLocality(局所性)。 金利デリバティブズのヘッジ商品は、通常カーブ構築に使ったベンチマーク商品を使います。あるポジションのヘッジ比率を計算する際、ヘッジ対象の満期に近いヘッジ商品だけでヘッジが可能か、それともカーブの広範囲にわたってヘッジ商品が必要になるのか?
こうやってみると、Forward Curveの形状と、局所性が問題になりそうです。これらについて、様々なInterpolation法で、それぞれどうなっているのか検証し、選択の際の判断基準とする必要があります。
様々なInterpolation法を分類する場合、(i) 各Pillarにおける“何を”繫ぐのか? (ii) どのような“関数形”で繫ぐのか? でカテゴリー分けが出来ます。 (i)については、次の様な値が考えられます。
- Par Rate
- Discount Factor
- Zero Coupon Rate
- Discount Factorの対数
- Zero Coupon Rateの対数
- 瞬間フォワード金利
この内、Par RateやDiscount Factorについては、どのように補間しても、そこから導出されるForward Rate Curveが非常に不自然な形になるので、実務で使われる事はまずありません。その他の選択肢については、次の、Interpolatorの関数形との関連で考える必要があります。 (ii)については、Interpolatorの関数形で分類できます
- 1次式(Linear Interpolation)
- 2次の多項式(Quadratic Splines)
- 3次の多項式(Cubic Splines)
- 4次より高次の多項式
- B-splines
この内、4次より高次の関数は、実務で使われることは殆どないと推察しています。カーブを滑らかにし過ぎると、Pillar間で不自然な波が発生したり、局所的な最小値、最大値が、Pillarの値から大きく離れてしまい、おおきな“たわみ”が発生したりするからです。
実務では、3次のスプライン関数(Cubic Spline)を使うのが多数派かと思いますが、一次式の方法も、シンプルさと局所性が優れている事から、捨て去られている訳ではありません。2次の多項式や、B-Splineの方法も、非常に技巧的な修正を加えて使う方法が紹介されています。
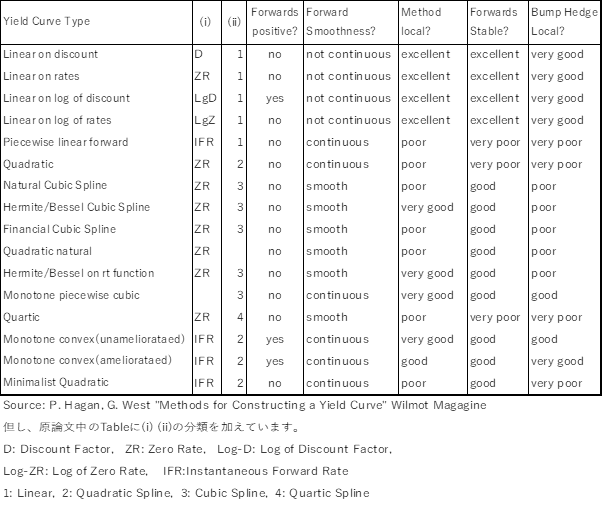
(i),(ii) の選択肢の組合せと、上記の望ましい性質との対応関係を表にしたものが、Hagan-Westの2007年の論文(”Methods for Constructing a Yield Curve” P. Hagan, G. West, 2007, Wilmot Magazine)に掲載されています。様々なInterpolation法と、その性質が俯瞰できるので、参考になると思います。