実務で使える金融工学　実践編

２.　"Implementing QuantLib"の和訳

Chapter-VII The Tree Framework: Tree　を使った価格モデルのフレームワーク

7.1 The Lattice and Discretized Asset classes： 格子クラス および 離散化資産クラス

Tree フレームワークにおける主要な２つのクラスは、Latticeクラス および Discretized Assetクラス です。このクラスの内容を下記 Lisint7.1 に示します。 

Listing 7.1：Latticeクラス と DiscretizedAssetクラス の実装 

class Lattice {
      public:
        Lattice(const TimeGrid& timeGrid) : t_(timeGrid) {}
        virtual ~Lattice() {}

        const TimeGrid& timeGrid() const { return t_; }

        virtual void initialize(DiscretizedAsset&, Time time) const = 0;
        virtual void rollback(DiscretizedAsset&, Time to) const = 0;
        virtual void partialRollback(DiscretizedAsset&, Time to) const = 0;
        virtual Real presentValue(DiscretizedAsset&) const = 0;

        virtual Disposable<Array> grid(Time) const = 0;
      protected:
        TimeGrid t_;
    };
class DiscretizedAsset {
      public:
        DiscretizedAsset()
        : latestPreAdjustment_(QL_MAX_REAL),
          latestPostAdjustment_(QL_MAX_REAL) {}
        virtual ~DiscretizedAsset() {}

        Time time() const { return time_; }
        Time& time() { return time_; }
        const Array& values() const { return values_; }
        Array& values() { return values_; }
        const shared_ptr<Lattice>& method() const {
            return method_;
        }

        void initialize(const shared_ptr<Lattice>& method, Time t) {
            method_ = method;
            method_->initialize(*this, t);
        }
        void rollback(Time to) {
            method_->rollback(*this, to);
        }
        void partialRollback(Time to)  {
            method_->partialRollback(*this, to);
        }
        Real presentValue() {
            return method_->presentValue(*this);
        }

        virtual void reset(Size size) = 0;
        void preAdjustValues() {
            if (!close_enough(time(),latestPreAdjustment_)) {
                preAdjustValuesImpl();
                latestPreAdjustment_ = time();
            }
        }
        void postAdjustValues() {
            if (!close_enough(time(),latestPostAdjustment_)) {
                postAdjustValuesImpl();
                latestPostAdjustment_ = time();
            }
        }
        void adjustValues() {
            preAdjustValues();
            postAdjustValues();
        }

        virtual std::vector<Time> mandatoryTimes() const = 0;

      protected:
        bool isOnTime(Time t) const {
            const TimeGrid& grid = method()->timeGrid();
            return close_enough(grid[grid.index(t)],time());
        }
        virtual void preAdjustValuesImpl() {}
        virtual void postAdjustValuesImpl() {}

        Time time_;
        Time latestPreAdjustment_, latestPostAdjustment_;
        Array values_;

      private:
        shared_ptr<Lattice> method_;
    };

void DiscretizedAsset::initialize(const shared_ptr<Lattice>& method,Time t) {
	method_ = method;
	method_->initialize(*this, t);
}

void DiscretizedAsset::rollback(Time to) {
	method_->rollback(*this, to);
}

void DiscretizedAsset :: partialRollback (Time to) {
	method_->partialRollback(*this, to);
}

Real DiscretizedAsset :: presentValue() {
	return method_->presentValue(*this);
}

void DiscretizedAsset :: preAdjustValues() {
	if (!close_enough(time(),latestPreAdjustment_)) {
		preAdjustValuesImpl();
		latestPreAdjustment_ = time();
	}
}

void DiscretizedAsset :: postAdjustValues() {
	if (!close_enough(time(),latestPostAdjustment_)) {
		postAdjustValuesImpl();
		latestPostAdjustment_ = time();
	}
}

void DiscretizedAsset :: adjustValues() {
	preAdjustValues();
	postAdjustValues();
}

bool DiscretizedAsset :: isOnTime(Time t) const {
	const TimeGrid& grid = method()->timeGrid();
	return close_enough(grid[grid.index(t)],time());
} 

我々の当初の意図は、Latticeクラスを、離散的な格子構造の概念をより広範にモデル化したものとして、Treeモデルでも Finite Differenceモデル（有限差分法）でも使えるようにしたいというものでした。しかし、実際にはそのようになりませんでした。Finite Difference法のフレームワークは独自の方法で構築されて行き、Latticeクラスに統合されていく事は当面無いと思われます。しかし、当初そのようにデザインしようとしたおかげで、Latticeクラスの構造は明瞭です。今の所、この（抽象）クラスに、派生クラスで行うべき実装は含まれておらず、また Treeクラスに対する依存もありません。 

Latticeクラスのコンストラクターは、TimeGridクラスのインスタンスを引数として取り、それをメンバー変数に保存します（これは、TimeGridを返すインスペクター関数 とともに、唯一の「実装は継承クラスで（行うべき）」に対する例外です）。　それ以外のメソッドはすべて純粋仮想関数です。initialize( )メソッドは、引数で与えららた時間を使って、Lattice上に Discretized Assetを設定します。（注：この段階では、（各メソッドが抽象的なので）ほとんど身振り手振りで説明しているようなものと認識しています。具体的なLatticeインスタンスの説明にまで進めば、もう少し明確になってくると思います。）　rollback( ) と partialRollback( )メソッドは、対象資産（の価格）を Lattice に沿って指定された時間まで遡って行きます（２つのメソッドの違いは後で説明します）。presentValue( )メソッドは、関数名が示す通りの値を返します。 

最後に grid( )メソッドは、Lattice上の離散化した対象資産の価格を返します。このメソッド（の宣言の仕方）は、若干問題を含んでいます。この情報は、Libraryの中の他の所で必要でしたが、開発当時、この方法より良い解決策は浮かびませんでした。その結果、このメソッドは明らかな弱点を持っています。まず、このメソッドは戻り値の型を指定していますが （訳注：Disposable＜Array＞）、これにより実装の漏れが発生するか、あるいは型変換を強制する事になります。また、Latticeが ２ファクター以上の確率変数を取り扱う場合は、このメソッドは全く意味を成しません。なぜなら、そのようなケースでは、Latticeの格子構造は、行列あるいは立方行列の形にしなければなりません。実際の所、２ファクターの Lattice を取り扱う場合、このメソッドは例外処理に飛ぶように実装されています（訳注：すなわち使えないようにしている）。という事で、このメソッドは将来 Library のバージョンアップの際、大幅な見直しが必要です。 

DiscretizedAssetクラスは、Treeフレームワークにおける、Latticeクラスの重要な相方になります。Latticeがアボットとすれば、これはコステロになります。（訳注：アボットとコステロは、米国のコメディアンのペア）　このクラスは、Lattice上で価格を計算される資産 （訳注：その離散的な価格分布） をモデル化したものです。このクラスは、Latticeクラスと協働しながら、汎用的な動作を提供するとともに、派生クラスにおいて、個別の商品に特有な動作を実装するための接続ポイントをいくつか用意しています。 

上記Listingを見て分かる通り、このクラスは Latticeクラスほど抽象的ではありません。殆どのメソッドは具体的に実装されていますが、いくつかの仮想関数はTemplate Methodパターンを使って、（派生クラスで）動作を加える事が出来るようになっています。 

コンストラクターは、引数を取りませんが、２つの内部変数の初期化を行います。インスペクター関数は、Lattice上のデータを返します。すなわち、Lattice上のある Node における時間 t と、その時点 t における資産価格（訳注：離散的な資産価格の配列）です。いずれのインスペクター関数とも、データに対する読込み用と（訳注：const宣言されている方）、書込み用が用意されており、後者を使えばLatticeの実装の際に、データ内容を修正できます。時間軸に沿って資産価格の計算を行う Latticeインスタンスを返すインスペクター関数は、読込み専用です。 

その次のメソッド群は、どの派生クラスでも使える共通の動作を実装しており、ユーザーが自身のプログラムの中で利用する際のインターフェースを提供しています。Treeを使った Pricing Engine の中身は、Tree と Discretized Assetクラスのインスタンスを生成した後に、通常、次のようなコードを含むものになると想定されます。 

    asset.initialize(lattice, T);
    asset.rollback(t0);
    results_.value = asset.presentValue();

initialize( )メソッドは、価格計算で使われる Lattice インスタンスを引数で取ってきて （その前に、Latticeが持つTimeGrid(時間軸)の情報には、mandatoryTimes( )メソッドを使って、必ず含めるべき時点の情報を加えておく必要があります）、（離散的な）資産価格の初期値をその上に設定します（むしろ、最後の価格と言った方がいいかもしれません。引数で渡される T はオプション期日を意味しているので）。rollback( )メソッドは、Lattice上で、（離散的な）資産価格を t=0 （現時点）まで遡って計算していきます。そして presentValue( )メソッドは、その資産価格を、単一の値として取りだします。 

上記 3種類のメソッドは、一見単純そうにみえますが、実装内容は Discretized Assetクラスでも Latticeクラスでも相当な量の動作が記述されており、かつ両方のクラスが用意する他の殆どのメソッドが関与します。この２つのクラスの相互に協働する様子は、Who’s on First （訳注：AbbotとCostelloのコメディーでファーストの守備をしている選手の名前が Who というので、会話のやりとりがコミカルに進展していくもの） ほど滑稽ではありませんが、大変複雑で、それをトレースしていくのは相当大変です。少しでも理解しやすくするため、以下のチャートをご覧ください。 

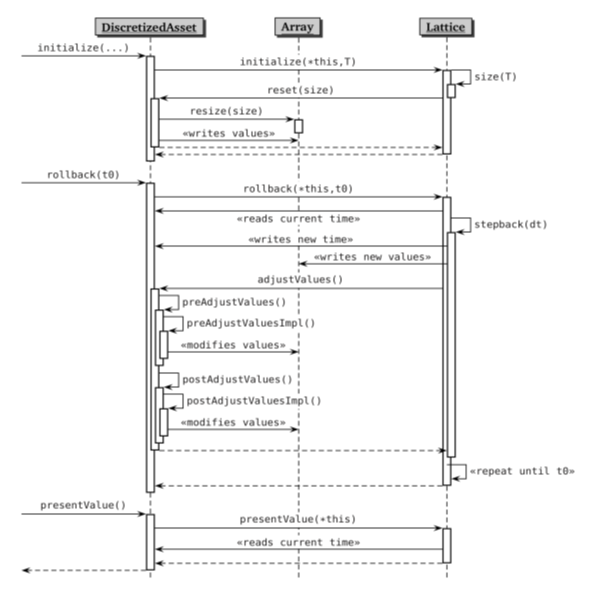
initialize( )メソッドは、まず Lattice 上の最終期日に資産価格（の配列）をセットし、そこから Lattice を遡って計算できるように準備を整えます （'Lattice上の最終期日'とは、'資産の最終期日'の意味です）。この意味は、まず資産価格を保持する Lattice 上の Node 配列 は、正確に dimension されなければなりません（訳注：資産価格の配列の‘要素数’と‘正しい間隔’の設定）。かつ、そこに正しい資産価格を設定しなければなりません。initialize( )メソッドは、DiscretizedAssetクラス内のメソッドの大半がそうであるように、実際の動作の一部を Latticeクラスに委託しています。つまり、このメソッドの動作内容は、Latticeインスタンスをメンバー変数に代入した後、Latticeの initialize( )メソッドに、最終期日と自分自身のポインターを引数にして、呼びだすのみです。 

Latticeベースクラスでは initialize( )メソッドは純粋仮想関数として宣言されており、実装されていません。しかし、きちんと作動するメソッドを派生クラスで実装するには、上記のフローチャートにある通り、プロセスの複雑なやりとりを記述する必要があります。このチャートには示していませんが、まず、いくつかの事前準備を整える必要があるでしょう。そのひとつは、最終期日における Lattice のサイズ （すなわち離散的な資産価格の配列数）を決める事です。その為には、おそらく、対応するメソッドを呼び出す事になるでしょう。次に、DiscretizedAssetインスタンスに、その最終期日をコピーし （注：このクラスは読込みと書込みができるメソッドを用意していた事を思い出して下さい）、そのサイズを（すなわち離散価格の配列数を） DiscretizedAssetクラスの reset( )メソッドに渡します。派生クラスで実装される reset( )メソッドは、そのサイズに従って対象資産価格の配列を調整し、その資産に特有の値を設定します（例えば債券であれば、償還価格と最終クーポン）。 

次に、rollback( )メソッドです。同じように、このメソッドも Latticeクラスの同じ名前のメソッドを呼び出し、それが Latticeの時間軸を順番に遡って計算していく重たい作業を実行していきます。このメソッドは、まず DiscretizedAssetクラスが持つ'時点'の情報を読み、それによってLattice上のどの時点の Nodeを計算しているかを確認し、そこから密接な協働がスタートします。 

ここで重要なポイントは、Latticeが時間軸を遡るにあたって、クーポンの支払いやオプションの期限前行使など、様々なイベントが発生することがあり、単純に資産価格遡って計算するだけではすまないという事です。従って、まずTreeを一段階ずつ遡り、そこで資産価格を修正し（修正にはNodeが縮合していく操作と現在価値への割引の操作も含まれます）、さらに DiscretizedAssetインスタンスに対して、何等か追加の修正が必要無いか確認します。確認の方法は DiscretizedAssetクラスの adjustValues( )メソッドを呼び出して行われます。 

その修正の操作は、preAdjustValues( )メソッド呼び出しと postAdjustValues( )メソッド呼び出しの、２段階で行われます。２段階で行う理由は、その間に、他の資産の価格修正を行う機会を与える為です。この動作については例を使って後程説明します。この２つのメソッドはそれぞれ若干の事前準備の操作を行った後、商品の特性に合わせて実装されている仮想関数 （preAdjustValuesImpl( )とpostAdjustValueImpl( )） を呼び出します。（注：事前準備とは、まず直近の修正を行った時点の情報を保持し、同じ時点で修正を２回行わないようにする事です。対象資産が複数になった場合、こういった事が起こり得るので、そうなると計算結果をめちゃくちゃにしてしまいます） 

この操作が終了すると、ボールは Lattice側に返ってきます。Latticeはさらに１段階、時間を遡り、同じ動作を何度も繰り返し、最終的に目標とした時点まで遡ります。 

最後に、presentValue( )メソッドは、もちろん、（対象）資産の現在価値を返します。このメソッドは、ユーザーのプログラムコードから呼び出される事を想定して設計されています。呼び出されるタイミングは、資産価格を遡って計算する動作が、特殊な修正をもはや必要としない時点に到達した時です。特殊な修正を必要としないとは、そこから先の修正は現在価値への割引のみであるという意味です。例えば、一番最初に来るオプション行使期日とか、債券であれば最初のクーポン日です。これまでと同様に、DiscretizedAssetクラスは、その動作を Latticeクラスの presentValue( )メソッドに委託しています。具体的な Latticeの派生クラスでは、モデルによって、Lattice を単純に現時点まで遡って Node のスタート時点の資産価格の値を読み込むか、あるいは近道を通って現時点の（訳注：先ほどの資産価格を遡る動作が、特殊な修正をもはや必要としない時点のこと） Node の資産価格をもとに現在価値を計算する関数を使う事もあります。 

以上のフレームワークには、当然、修正の余地があります。一部の動作は、その必要性が黙示的にしか示されていません。例えば、Latticeクラスの initialize( )メソッドは、DiscretizedAssetクラスの reset( )を呼び出さなければならないとか、reset( )メソッドは DiscretizedAssetクラスが保持している （資産価格の） 配列のサイズを修正しなければならないといった点です。しかし、現時点では、これが Library が提供しているものの実態です（訳注：従って、そのように使って頂くしかありません）。では、次に進んで、いくつかの DiscretizedAssetインスタンスを構築してみましょう 

 

 

<ライセンス表示>

QuantLibのソースコードを使う場合は、ライセンス表示とDisclaimerの表示が義務付けられているので、添付します。   ライセンス