1. QuantLibを使ってみる
1.2 Example を試す
1.2.6 : BermudanSwaption : 3種類のShort Rate Modelを使ったバーミューダン・スワップションの価格評価
1.2.6.1 はじめに
このExampleは、3種類の Short Rate Model (G2++、Hull-White、Black-Karasinski) を使って、バーミューダン・スワップションの価格評価を行っています。
前のExample"CallableBond"でも、バーミューダンタイプの Call Option 付き債券の価格を、Hull-Whiteモデルによる3項Tree を使った価格エンジンを使って導出しました。しかしそこでは、モデルのVolatilityパラメータについて、Calibrationで求めるのではなく、適当な値を外生的に与えていました。
ここでは、3種類の Short Rate Model それぞれについて、モデルパラメータを、市場データに Calibration してから、価格評価を行っています。Calibration する事により、バーミューダン・スワップションを始めとするエキゾチック商品のリスク量を、Swaption や Cap/Floor といったプレーンな商品と相対化して計測する事ができ、エキゾチック商品のリスクを、プレーンな商品で(ある程度まで)ヘッジする事が可能になります。そういう意味で、実務でパラメトリックなモデルを使う場合、パラメータの Calibration は必須です。
Short Rate ModelのパラメータCalibrationは、2つの別々のアルゴリズムからなります。ひとつは、イールドカーブに、中心回帰レベルをフィットさせるアルゴリズムで、もうひとつは、ベンチマーク金利オプションの市場価格(またはImplied Volatility)に、中心回帰強度とVolatilityパラメータをフィットさせる事です。このExampleで例示されているのは、後者の方のアルゴリズムです。前者のイールドカーブへのフィットは、価格エンジンの中に組み込まれており、価格エンジンを起動するたびに、自動的に行われています。
Short Rate Model のパラメータの Calibration については、上級編“Hull-Whiteモデル:モデルパラメータのCalibration”で解説しているので、そちらもご覧ください。
Short Rate Model のファミリーは、瞬間短期金利の確率過程を記述するもので、1ファクターモデルの場合、基本的に下記のような確率微分方程式で記述されます。
\[ dr(t)=k(t)(θ(t)-r(t))dt+σ(r,t)dW(t) \]但し
\(r(t)\) : 瞬間短期金利
\(k(t)\) : 中心回帰強度
\(θ(t)\) : 中心回帰レベル
\(σ(r,t)\) : 拡散係数(Volatility)
\(dW(t)\) : ウィーナー過程
上の式は、Short Rate Model を一般化した表記方法で、各パラメータ係数の違いが、個別の Short Rate Model を特徴付けます。
Hull-White モデル(拡張 Vasicek モデルとも呼ばれています)は、中心回帰強度 \(k(t)\)、拡散係数 \(σ(r,t)\) をそれぞれ定数 \(k,~~σ\) と仮定したモデルです。すると、\(r(t)\) はガウス分布するので、Gaussian Short Rate Model のグループに属します。Hull-White モデルは、Short Rate Model の中でも比較的シンプルで、将来のゼロクーポン債価格や、ヨーロピアン・オプション価格が解析解で求まり、使い易いのが特徴です。但し、瞬間短期金利 \(r(t)\) がマイナスになる可能性があり、それが欠点とされていました。(マイナス金利が日常化した現在では、もはや欠点とは言えませんが。)
Black-Karasinski モデルは、中心回帰強度 \(k(t)~を定数~k~ と見做し、拡散係数~σ(r,t)~を、σr(t)\) と仮定したモデルです。すると、\(r(t)\) は、対数正規分布する事になります。このモデルでは、\(r(t)\) がマイナスになる事が無いので、当初はそれが Hull-White モデル対する優位点とされていました。但し、このモデルからは、ゼロクーポン債価格や、オプション価格が解析的に求まらず、価格計算には3項Tree などを使って、数値的に(近似値を)求める必要があります。90 年代に、実務でも使われていたようですが、主要国で超低金利、あるいはマイナス金利が状態化した今、このモデルをそのままの形で使っている所は無いと思います。
G2++モデルは、確率変数が2ファクターの Short Rate Model で、瞬間短期金利 \(r(t)~が2つの確率変数~x(t),~y(t)~とイールドカーブへのフィッティングパラメータ~φ(t)\) の和として、下記のような確率微分方程式で表現されるモデルです。
\[ \begin{align} & r(t)=x(t)+y(t)+φ(t), \\ & dx(t)=-a x(t)dt+σ dW_1 (t),~~~~~~ x(0)=0 \\ & dy(t)=-b y(t)dt+η dW_1 (t),~~~~~~ y(0)=0 \\ & Corelation(dW_1 (t),~dW_2 (t))=ρ dt \end{align} \]\(dx~と~dy~\)はいずれも 0 に中心回帰するドリフト項と、それぞれ\(σ,~η\) の Volatility 係数を持つ拡散項で記述されています。このモデルのパラメータは、\(φ(t),~a,~b,~σ,~η,~ρ\) で、\(φ(t)\) はイールドカーブにフィットするように Calibration され、\(a,~b,~σ,~η,~ρ~\) は、市場の Volatility データに Calibration されます。この Example では、後者の Calibration を行っています。
Short Rate Model については、すでにある程度理解されているという前提で話を進めるので、ここでは、これ以上詳しく解説しません。Hull-White モデルについては上級編“Hull-Whiteモデル”を参考にして下さい、また G2++ については、Brigo-Mercurio “Interest Rate Models”(2006, Springer)に詳しく解説されています。
この Example では、いずれのモデルのパラメータも、時間に依存せず、定数と仮定されています。パラメータを時間の関数(通常は、Piecewise Constant な関数と仮定される)とすれば、市場データへのフィットは良くなりますが、デメリットも多くあります。実務では、定数と仮定して使う事の方が多いように思います。時間に依存する関数と仮定して Calibration する方法は、Gaussian1DModel の Example で解説する予定です。
1.2.6.2 ソースコードのコンパイルと実行
これまで通り、ソースコードのビルドの方法から説明します。QuantLib のインストール方法を解説したセクションですでにビルドしていれば、再ビルドは必要ありません。もし、ビルドが済んでいない場合は、次の手順で、Debug モードでビルドし、試しに実行してみて下さい。
- QuantLibのファイルFolder の Examples ディレクトリから、BermudanSwaption のディレクトリを探し、そこにあるプロジェクトファイル(BermudanSwaption.vcxproj)をダブルクリックして開けます。Visual Studio が起動され、このプロジェクトファイルが開かれる。
- ソリューションエクスプローラーに表示されているプロジェクトファイルのディレクトリを展開し、SourceFiles のフォルダーにある CallableBonds.cpp をクリックします。すると約 420 行あるソースコードが開かれます。
- きちんと動作するか、まず確認してみる。メニューバーから ビルド → ソリューションのビルド を選択。ビルド が開始されます。既にビルド済みであれば、この操作は必要ありません。(当初、複数のプロジェクトをまとめている QuantLib.sln をビルドした場合、個別のプロジェクトにおける main() 関数を走らせる必要があります。その場合は、ソリューションエクスプローラーwindow から、該当のプロジェクト(ここではBermudanSwaption.)をクリックした上で、メニューバーから プロジェクト → スタートアッププロジェクトに設定 を選択して下さい。)
- エラー無くビルドが正常終了すれば、試しにプログラムを走らせてみます。メニューバーの デバック → デバックの開始 を選択。下記の コンソール画面が出力されれば成功です。 (但し、プログラムが終了すると同時に コンソール画面も消えてしまうようであれば、メニューバーから、 ツール → オプション → デバック → 全般 を選択し、「デバックの停止時に自動的にコンソールを閉じる」のチェックボックスをはずします。)
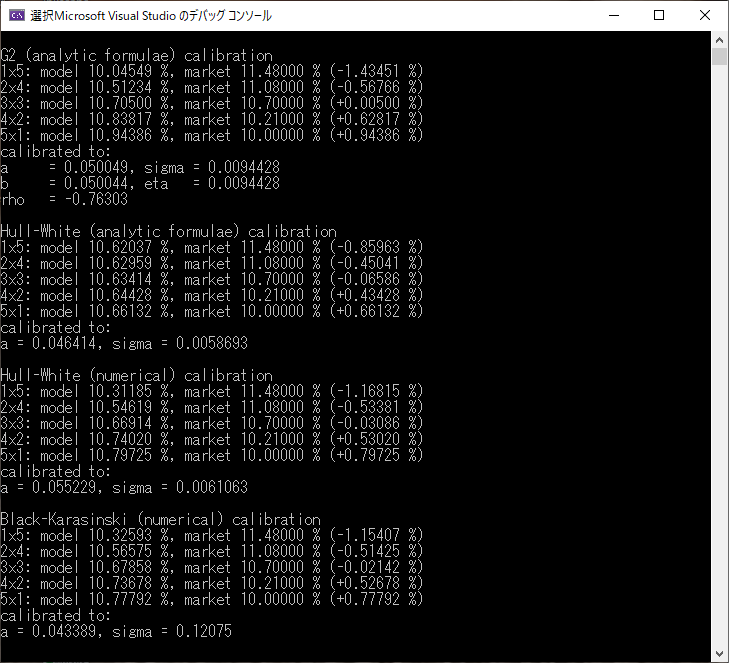
- 下記の コンソール画面にある通り、この例では、まず3種類の Short Rate Model を、(市場の)Black VolatilityデータにCalibration します。Calibration の結果、導出された各モデルのパラメータと、Black Volatility との誤差は画面出力の通りです。
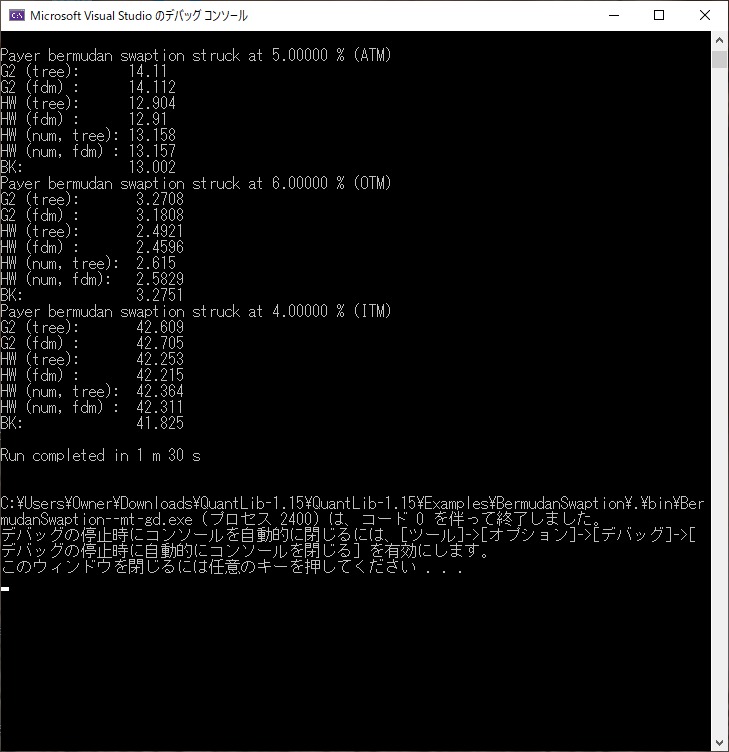
- Calibration 後、各モデルを組みこんだ価格エンジンを使って、3種類のバーミューダン・スワップションの価格計算をしています。G2++ モデル、及び Hull-White モデルでは、3項Tree を使ったアルゴリズムと、有限差分法を使ったアルゴリズムの、2種類の価格エンジンを使っています。Black-Karasinski モデルでは、3項Tree の価格エンジンのみを使っています。
- 計算時間は、1分30秒かかっています。おそらく、計算時間の多くは、G2++ モデルの価格エンジンのアルゴリズムによるものと推察されます。2ファクターモデルになるので、有限差分法や3項Tree のアルゴリズムでは、1ファクターモデルと比べて、Nを時間軸のステップ数とすると、\(O(N^2)\) のオーダーで計算時間がかかります。
1.2.6.3 ソースコードの解析
では、ここからソースコードを解析していきます。BermudanSwaption.cpp のファイルを、Visual Studio で開くか、面倒であれば、こちら“BermudanSwaptionCpp.html”を開いてください。
< プログラムコードの全体像 >
ますソースコードの全体像を俯瞰します。
全体で420行弱ありますが、main() 関数は 100 行目からで、その前に Calibration 用のローカル変数とローカルメソッドを定義しています。あくまで、この Example だけの為に用意されたもので、他では使えません。ローカル変数は、Calibration の対象となる、ヨーロピアン・スワップションの Black Volatility データを(行使期日×対象スワップ期間の2次元データとして)ハードコードで用意しています。ローカルメソッド calibrateModel( ) は、それを使って、 Model オブジェクトから calibrate() を呼び出し、結果をコンソール画面に出力するように定義されています。
main( )関数では、最初の 60 行程度を使って、価格計算対象となる商品オブジェクトと、価格エンジンの「部品」を生成しています。
次に、モデルの Calibration を行っています。まず 169~207 行目で、Calibration の準備をし、212~259 行目で、3種類の Short Rate Model それぞれについて、Calibration の実行と、結果のコンソール画面出力を行っています。
最後に、264 行目から、Calibration されたモデルを使って バーミューダン・スワップションの価格計算を行っています。
Calibration のアルゴリズムは、
-ベンチマーク商品(ここではヨーロピアン・スワップション)の価格を、
-ベンチマークモデル(ここではBlack、モデル) と
-Calibration 対象となるモデル(ここでは3種類のShort Rate Model)で計算し、
-その差が最小となるようなパラメータを求めます。
いわゆる最小値問題で、それを Solver のアルゴリズムを使って求めます。2つのモデルでの価格計算機能を担っているのが、CalibrationHelper オブジェクトで、さらにこのオブジェクトは、最小値問題における目的関数を提供する役割を負っています。この例では、Calibration の対象がヨーロピアン・スワップションなので、その派生クラスである SwaptionHelperオブジェクトを使っています。
モデルパラメータの Calibration が終われば、それぞれのモデルを使って、バーミューダン・スワップションの価格エンジンを生成し、価格評価を行います。このステップは、これまでの Example と同様、価格評価の対象となる商品オブジェクトと、計算アルゴリズムを担う価格エンジンオブジェクトを、それぞれその部品から生成し、組み立てていきます。
バーミューダン・スワップションの価格計算は、解析解では求まらず、有限差分法や3項Tree といった数値解を求めるアルゴリズムが必要になります。この Example では、G2++ と Hull-White モデルについては、有限差分法を使ったアルゴリズムと3項Tree を使ったアルゴリズムの2種類の価格エンジンをテストしています。Black-Karasinski モデルについては、3項Treeを使った価格エンジンのみをテストしています。
モデルオブジェクトと価格エンジンオブジェクトの関係について、念のため再確認しておきます。(オプション)モデルは、株価や金利といった確率変数が、ランダムに拡散していく様子を、確率微分方程式の形で表現したものを意味します。そのモデルから、確率変数の将来の分布が導出できます。その確率分布を使ってキャッシュフローやPayoffの期待値を計算するアルゴリズムが価格エンジンになります。期待値の計算方法は、幾通りもあり、ひとつのモデルで、複数の価格エンジンが存在します。様々な文献で、(あるいは自分も含めて)モデルを価格計算アルゴリズムと同義で使う表現をしばしばみかけますが、混乱しないようにして下さい。以下の説明でも、モデルオブジェクトと価格エンジンオブジェクトを、それぞれの役割を持つオブジェクトモデルとして解説します。
< ステップ毎のコード解析 >
では、ソースコードをステップ毎に説明します。
① 事前準備 1
main() 関数の前に、ローカル変数とローカルメソッドを定義しています。
まず 66~71 行目で、ヨーロピアン・スワップションの Black Volatility データをハードコードで用意しています。(コードではBlack Volと表記していませんが、後々のコードを見ればそれが分かります) ここでは、行使日が1年~5年、対象スワップ期間も1年~5年で、5×5のデータが用意されています。
73~98 行目で、calibrateModel() というローカルメソッドを定義しています。このメソッドは、引数として (i) Calibrationの対象となる“モデルオブジェクト” と、 (ii) Calibrationの目的関数を提供する“CalibrationHelperオブジェクト(の配列)” を取ります。このメソッドは、まず最初に、多次元ソルバーを生成します。77 行目の LevenbergMarquardt オブジェクトがそれです。この行にあるように、このクラスのインスタンスを生成するだけで、QuantLib が用意した、Levenberg-Marquardtタイプの多次元 Solver が簡単に使えます。(QuantLibでは、これ以外にもいくつか多次元Solverを用意しています)
78 行目で、モデルオブジェクトから、calibrate( ) メソッドを呼び出し、それに渡す引数として、(i) 目的関数(CalibrationHelperオブジェクト)、(ii)Solverと、(iii)Solverの終了条件(End Criteria)、 を指定します。後は、このメソッドが Calibration のアルゴリズムを実行してくれます。中で、相当複雑なアルゴリズムが走っていますが、ユーザーはその内容を知らなくても、これだけで Calibration が実行出来ます。
後は、Calibration の結果をコンソール画面に出力する為の操作になります。出力内容は、上記のコンソール画面出力をご覧下さい。
② 事前準備 2
100 行目からmain()関数が始まりますが、これまでの Example 同様、全体を try{ } でかこみ、{ } 内でエラーが発生すれば、408 行目以降の例外処理に飛ぶようになっています。
また、104 行目でboost::timerを起動しています。計算時間は、私のPCで1分30秒かかりました。
③ Evaluation Dateの設定
107~110 行目で、本日の日付けと、時価評価日を設定しています。2002 年 2 月と、ずいぶん古い日付けですが、この Example が作成された頃なのでしょう。決済日は、市場慣行に則り、2営業日後になっています。しかし時価評価日は本日に設定しています。イールドカーブの形状によっては、この差が微妙な価格差になるので、注意が必要です。
④ イールドカーブの生成
113~117 行目で、イールドカーブオブジェクトを生成しています。ここは、イールドカーブ構築のテストが目的では無いので、テストデータとしてシンプルな FlatForward オブジェクトを生成しています。113 行目で、4.875825% の値を外生的に与えていますが、これは、連続複利での表記であり、年1回払いのレートに換算すれば、5% p.a.に相当します。このイールドカーブは、金利スワップの部品になると同時に、価格エンジンにも組み込まれます。金利が期間構造の全期間に渡り一定なので、Interpolation や Bootstrapping などの操作を使って組み立てる必要はありません。
⑤ バーミューダン・スワップションの対象スワップの生成
バーミューダン・スワップションオブジェクトを生成する前に、まず 120~166 行目で、その対象スワップを生成しています。MulticurveBootstrapping の所で既に説明した通り、商品オブジェクト(ここではVanillaSwap)を作る為に、まずその部品から作ります。120~139 行目がそれです。部品は見ての通り、スワップの Cash Flow の日付けと金額を特定する為に必要な情報です。
141 行目で生成している VanillaSwap オブジェクトは、ダミーです。対象スワップは、フォワードスタートになるので、そのスタート時点で At the Money になるようなスワップレートをイールドカーブから計算するためのものです。FlatForwardのイールドカーブを使っているので、無駄な手順のようにも思えます。しかし、実際のフラットでないカーブの市場データを使う場合、At the Moneyの、先日付スタートのスワップレートを導出するには、必須の手順です。
152行目から、バーミューダン・スワップションの対象となる3種類(At the Money、Out of the Money、In the Money)の Vanilla Swap オブジェクトを生成しています。
⑥ Calibration Helper オブジェクトの生成
169行目から、この Example の肝である、CalibrationHelper オブジェクトを、部品から生成し、組み立てています。Calibration は、市場価格が観測可能なベンチマーク商品の集合に対して、
- 対象となるオプションモデル(をベースにした価格計算アルゴリズム)での価格と、
- ベンチマークモデル(通常はBlackモデル)をベースにしたオプション価格公式を使った価格
との差が、最小になるようなモデルパラメータを探すアルゴリズムです。そのアルゴリズムの中で、CalibrationHelper は下記の様な、最小値問題の目的関数を提供します。
\[ f(a,b,…)= \sum_{i=1}^N \left[ BlackPrice_i (S,σ,K,r,..)~-~ModelPrice_i (S,σ,K.r;a,b,…)\right]^2 \](上記式の右辺で、オプションの価格差ではなく、Black Implied Volatilityの差を使ってCalibrationする方法もあります。むしろ、実務ではそちらの方が一般的です。)
従って、CalibrationHelper は、価格評価対象となるベンチマーク商品の商品オブジェクト(ここではヨーロピアン・スワップション)と、その価格を計算する 2 種類の価格エンジンを合体させたようなオブジェクトになります。これを、部品から作り、組み立てていきます。
まず、169~174 行目で、Calibrationの対象となるヨーロピアン・スワップションの行使日の配列を生成しています。
次に、176 行目で、CalibrationHelper オブジェクト(ここではその派生クラスであるSwaptionHelperオブジェクト)の配列を格納するローカル変数を生成します。そして 182~196 行目で、SwaptionHelper オブジェクトを生成し、その配列に格納しています。ここで生成されたヨーロピアン・スワップションは、行使日×対象スワップ期間が1年×5年、2×4、3×3、4×2、5×1の5個です。
SwaptionHelper オブジェクト生成する For ループの中で、各行使日(を年数換算したデータ)の配列も生成しています。その配列を使って、199行目で TimeGrid オブジェクトを生成しています。そこでは、行使日の配列と30という引数が渡されていますが、TimeGrid は、3項Tree の時間軸を格納するオブジェクトで、この後生成される価格エンジンの部品となります。
203~207 行目で、3種類の Short Rate Model のオブジェクトを生成しています。Hull-White モデルだけは、2つ生成していますが、その理由は、CalibrationHelper で使うヨーロピアン・スワップションの価格計算アルゴリズムで、2通りの方法(解析解の方法と、3項Treeの方法)を試す為です。いずれのモデルも、(114行目で生成した)イールドカーブオブジェクトを引数として渡されています。このイールドカーブに、モデルの中心回帰レベル \( θ(t) \) パラメータをフィットさせます。そのアルゴリズムは、モデルオブジェクトの中に内包されており、価格エンジンを呼び出す度に Calibration されますが、この Example からは見えません。
これで、VolatilityパラメータのCalibrationの準備が出来ました。
⑦ Calibrationの実行
CalibrationHelper(ここではSwaptionHelper)の準備が出来たので、いよいよ Calibration の実行です。212 ~ 259行目で、3種類の Short Rate Model それぞれについて(Hull-Whiteモデルについては、さらに2つに分けて)Calibration を実行し、結果をコンソール画面に出力しています。
最初に 212 行目で、G2++ モデルのパラメータの Calibration を実行しています。まず SwaptionHelper オブジェクトの配列に、それぞれ G2SwaptionEngine を設定します。215 行目で G2SwaptionEngine のコンストラクターに G2++ モデルオブジェクトと、2つの引数 6.0 と 16 を渡しています。この価格エンジンは、G2++ モデルから、数値積分のアルゴリズムを使ってヨーロピアン・スワップションの価格計算を行います。(212行目で G2(analytic formulae) という表記がありますが、若干誤解を招く表現です。) 217行目で、この Example の最初の方で定義したローカルメソッド calibrateModel( )を呼び出して、Calibrationが実行されます。実際のアルゴリズムは、78 行目にある通り、モデルオブジェクトから呼び出される calibrate(CalibrationHelpers, Optimizer, Endcriteria)メソッドで、実行されます。Calibration が無事に終われば、結果をコンソール画面に出力します。
次に、228 行目で、Hull-White モデルから導出される、Swaption の解析解を使った価格エンジンで Calibration を行います。価格エンジンの名前が、JamishidianSwaptionEngine となっていますが、これは、解析解が、Jamishidianトリックと呼ばれるテクニックを使って導出されたものだからでしょう。
さらに239 行目で、同じ Hull-White モデルでも、3項Tree を使う方法でヨーロピアン・スワップションの価格計算を行う価格エンジンで Calibration を行っています。
最後に、250 行目で Black-Karasinski モデルから、3項Tree によるアルゴリズムを使った価格エンジンで Calibration を行っています。
ここでは、各価格エンジンのアルゴリズムの中身については、解説しません。先ほど紹介した Brigo-Mercurio の文献などを参考にして下さい。QuantLib を使う場合、そういったアルゴリズムの内容を知らなくても、モデルと価格エンジンを、どうやって組み立てるかを理解すれば、QuantLib が提供している様々なオプションモデルと価格エンジンを使って、様々な商品の価格計算ができます。
⑧ バーミューダン・スワップションの価格計算
モデルパラメータの Calibration が終わったので、それを使ってバーミューダン・スワップションの価格計算を行います。
まず、バーミューダン・スワップションの商品オブジェクトを生成します。対象スワップは、3種類用意されていました。すなわち、対象スワップのストライクレートが、5%(At the Money)、6%(Out of the Money)、4%(In the Money)の3種類です。この情報に、さらにオプション行使日の情報(オブジェクト)などの部品を作ります。そして、280行目の
Swaption bermudanSwaption (atmSwap, BermudanExercise);で、商品オブジェクトが完成しました。
さらに、価格エンジンを生成し、この商品オブジェクトに設定します。
バーミューダン・スワップションの価格計算は、3項Tree や、有限差分法を使った数値解を導出するアルゴリズムが必要なので、Calibration で使った、ヨーロピアン・スワップション用の価格エンジンがそのまま使えません。この例でも、285~308 行目で、各モデルについて、有限差分法と3項Tree を使ったアルゴリズムを使った価格エンジンを設定しています。(Black-Karasinskiモデルだけは、3項Treeのみです。) そして、商品オブジェクトから NPV() メソッドを呼び出せば、価格が返ってきます。
同様の操作を、OTMとITMのバーミューダン・スワップションでも行っており、それぞれ計算結果をコンソール画面に出力しています。
以上のように、ここでも、QuantLibを使うには、商品オブジェクトと価格エンジンオブジェクトを部品から組み立ててしまえば、あとはQuantLibが用意している様々な価格計算アルゴリズムを、簡単に使えます。但し、このExampleにある様に、モデルのパラメータのCalibrationが必要な場合、その手続きは、この単純なExampleであっても相当複雑になります。
この例では、限られた数のヨーロピアン・スワップション(Co-terminal Swaptionとよばれるグループ)でCalibrationを行いました。しかし、実際にモデルのCalibrationを行う場合、そのモデルのパラメータの意味・役割を十分理解し、かつ価格評価の対象となる商品の特性も理解した上で、Calibrationのターゲットとなるベンチマーク商品を選ぶ必要があります。これは、モデルに対する深い知識と、市場データに対する深い理解があって初めて可能になるプロセスです。
<ライセンス表示>
QuantLibのソースコードを使う場合は、ライセンス表示とDisclaimerの表示が義務付けられているので、添付します。 ライセンス