上級編 4. Short Rate Models
4.4 Hull-White モデル
4.4.5 Trinomial Tree : 3項ツリーの構築
4.4.5.3 3項ツリー構築のアルゴリズム
では、具体的に、3項Tree構築のアルゴリズムについて説明します。
4.4.5.3.1 パラメータの特定
Hull-Whiteモデルにおける、3種類のモデルパラメータの内、\(θ(t)\) については、既に述べた通り、特定する必要はありません。モデルから導出されるイールドカーブが Arbitrage Free の条件を満たすようにする役割は、\(θ(t)\) から、\(x\) の調整パラメータ \( \phi (t) \) (4.37式の第2項)に移ります。\(\phi (t)\) は、ツリー構築の途中で導出します。
\(a(t),~と~ σ_r (t)\) は一旦仮りの数字を置いて、樹形構造が完成してから市場データに Calibration して求めます。実務では、3項ツリー構築のアルゴリズムをプログラムコードにする際、変数として定義しておき、それを使って樹形構造を作ります。後で、その値を自由に動かす事で、樹形構造の形状を伸縮させ、市場データへ Calibration 出来るように、プログラミングしておきます。
ちなみに、\(a(t),~と~ σ_r (t)\) の関数形は、階段関数のような形状の、Piecewise Constant 関数とするのが一般的です。さらに言えば、この内 \(a(t)\) の方は、全期間で一定の定数にする事も多いようです。式で表現すると、次の様な形になります。(\(I_{~}\) は Indicator function(指示関数)で、{ }内の条件が満たされた場合のみ 1 を返し、それ以外は 0 になる関数です。 )
\[ a(t)=\sum_{i=0}^{n-1} a_i~ I_{\{t_i< t < t_{i+1}\} },~~~~~~~~~ \sigma_r (t)=\sum_{i=0}^{n-1} σ_{r,i} I_{\{t_i< t< t_{i+1}\}} \tag{4.39} \]こうする事で、ツリーの時間軸の間では、一定の値 \(a_i,~~σ_{r,i}\) を取り、その間の確率変数の期待値(あるいはその近似値)や分散の計算が容易になります。
4.4.5.3.2 時間軸の設定
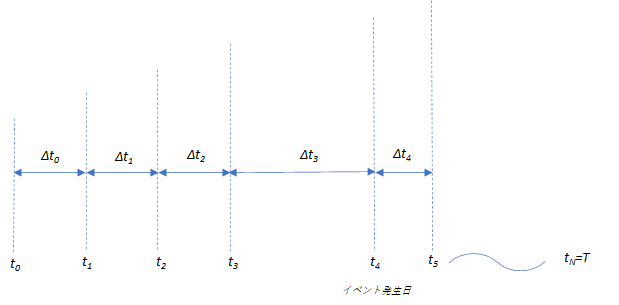
ツリーの時間軸を、現時点 \(t_0\) から最終期日 T まで、いくつかのポイントで分割します。最終期日は、オプションの最終行使日か、あるいは、対象資産の最終キャッシュフロー日になります(ゼロクーポン債価格の解析解が求まらないケースは後者になります)。 設定した時間軸と、その時間間隔を下記のように表記します。
\[ t(0)=t_0 < t_1 < t_2,…, < t_N =T,~~~~~~~~~~~~~~~Δt_i=t_{i+1}-t_i \]3項Treeでは、時間間隔は必ずしも同一間隔にする必要はなく、時間軸を柔軟に設定できます。また、最終期日Tまでに、対象商品のキャッシュフローが発生する日、オプション行使が可能な日、さらに、Calibration対象のベンチマーク商品の期日があれば、それらを時間軸に加えます。そういったイベント日のキャッシュフローをきちんと評価し、オプション行使の判断を適切に行えるようにする為です。
こうやって決まった時間軸の様子を図示します。
4.4.5.3.3 状態変数軸(\(x\) 軸)の離散化
時間軸が決まれば、各 \(t_i\) ごとに、\(x\) 軸の離散化を行います。すなわち、\(t_i\) 時において、各 \(x\) の間隔 \(Δx_i\)、及び \(x\) の取り得る値の最大値と最小値を決めます。この幅も、3項ツリーの場合は、柔軟に設定できます。広めに設定する方が、拡散の様子を、より少ないステップ数で表現できます。しかし、広くしすぎると、後ほど計算する遷移確率のいずれかがマイナスになるケースが発生します。Hull-White の論文(およびその他多くの文献)では、\(Δt_{i-1}=t_i-t_{i-1}\) 間の Volatility の \(\sqrt{3}\) 倍で設定する事を推奨しています。すなわち、
\[ Δx_i=σ_r (t_{i-1}) \sqrt{3 Δt_{i-1}} \tag{4.40} \]とします。
4.38の \(dx(t)\) の式を見ればわかる通り、0 が中心回帰レベルになっているので、\(x\) はプラスマイナス対称に拡散していきます。従って、すべての時間軸において中心となる \(x\) の値を 0 とし、そこからプラスマイナス対称に \(Δx_i\) ずつ離れた値を設定します。\(t_i\) 時における状態変数 \(x\) の座標インデックスを j とします。すると、3項ツリー上のすべてのノードの座標が t軸 のインデックス i と \(x\) 軸のインデックス j の組合せで表示できます。それをノード(座標) \((i,j)\) と表記し、そのノード上にある \(x\) の値を、\(x_{i,j}\) と表記します。
\[ x_{i,j}~~~~~~i=0,1,2,…,n~~~~~~j=0,±1,±2,…,±m \]すると、\(x_{i,0}\) が中心ノードとなり、すべての時間軸で、\(x_{i,0}=0\) となります。そこを中心として、\(t_i\) 時の \(x\) 座標の値がすべて特定できます。
\[ x_{i,1}=x_{i,0}+Δx_i,~~x_{i,2}=x_{i,0}+2Δx_i,~…~,x_{i,m}=x_{i,0}+mΔx_i,~~~~~~\\ x_{i,-1}=x_{i,0}-Δx_i,~~x_{i,-2}=x_{i,0}-2Δx_i,~…~,x_{i,-m}=x_{i,0}-mΔx_i, \]\(Δx_i\) の値に従って、状態変数軸の座標が特定される様子を下記の図に示します。
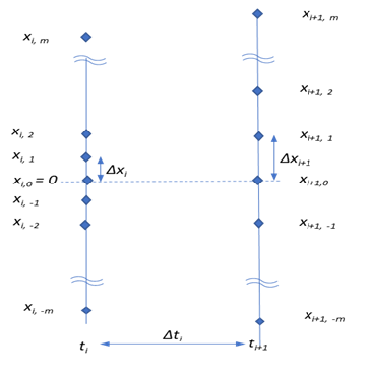
各時間軸での最大値と最小値、すなわち、\(x_{i,m}~と~x_{i,-m}\) は、次に説明する、ツリーの分岐方法を決める中で求まります。
4.4.5.3.4 3項Treeの分岐先インデックスの特定
時間軸と状態変数軸の座標が決まったので、次にそれをどのように繫いでいくかを決めます。
3項ツリーでは、ある時間軸 \(t_i\) 上のノード(座標) \(x_{i,j}\) から、次の時間軸 \(t_{i+1}\) 上の3個のノード \(x_{i+1,k},~~x_{i+1,k+1},~~x_{i+1,k-1}\) へ分岐させます。その分岐先は、分岐先での条件付き期待値と分散が、モデルで想定したものと一致するように決めていきます。一部の遷移確率がマイナスになっても構わないなら、どのノードに分岐しても期待値と分散を一致させる事は可能です。しかしマイナスの確率は概念としてあり得ないので、当然ながら、3項の遷移確率がすべて正にならなければなりません。その分岐先の中心ノードを、条件付き期待値に一番近くなる様に選択すれば、3ノードへの遷移確率がすべてプラスになるように出来ます。(とHull-Whiteなどの文献は述べていますが、その証明は見当たりませんでした。)
その様子を下記の図にすると下記のようになります。
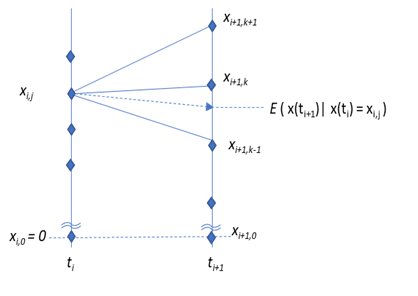
今、ノード \(x_{i,j}\) にいた場合、\(x~の~Δt_i\) 後の条件付き期待値は、下記式を(\(x_{i,j}\) を初期値として)\(t_i~~から~~t_{i+1}\) まで積分すれば求まります(積分後、\(dW\) による伊藤積分の項を除いた項がそれになります)。
\[ dx(t)=-a(t)x(t)dt+σ_r (t)dW, \]また条件付き分散は、Volatility 関数の 2乗を \(t_i~~から~~ t_{i+1}\) まで積分すれば求まります。
それぞれ、求めてみましょう。\(Δt\) 間のパラメータが定数(Piecewise Constant)であれば、下記のようになります。
\[ E \left( x(t_{i+1}) \vert x(t_i)=x_{i,j} \right) = x_{i,j} e^{-a_i Δt_i} =: M_{i,j} \tag{4.41} \] \[ Var \left( x(t_(i+1) )\vert x(t_i)=x_{i,j} \right) =\frac{σ^2}{2a}(1-e^{-2aΔt_i}) =:V_i^2 \tag{4.42} \]もし積分がうまく求まらない場合は、\(dx\) の式のドリフト項と拡散項の係数をそのまま使って、\(Δt\) 間の変化を線形で近似する方法もあります。Hull-Whiteの2000年の論文では、そうようにして、平均と分散を求めています。
\[ E \left( x(t_{i+1}) \vert x(t_i)=x_{i,j} \right) \approx x_{i,j}-x_{i,j}a(t_i)Δt_i =: M_{i,j} \tag{4.43} \] \[ Var \left( x(t_{i+1}) \vert x(t_i)=x_{i,j}\right) \approx σ_r(t_i)^2 Δt_i =:V_i^2 \tag{4.44} \](注 : 同論文では、\(x(t_{i+1})\) の条件付き期待値ではなく、\(dx\) (変化幅)の期待値を計算しています)
上の図では、\(x_{i,j}~~の~~Δt_i\) 後の条件付き期待値 \(M_{i,j}\) に最も近いノードが \(x_{i+1,k}\) であり、3項ツリーの分岐先は、それと、その上下のノードになります。
この考え方を使えば、分岐先の中心ノード \(x_{i+1,k}\) の x軸インデクス k を求める具体的な式は、下記の通りになります。
\[ k=round\left(\frac{M_{i,j}}{Δx_{i+1}}\right) \tag{4.45} \]上式中の round() は、括弧内を四捨五入する関数で、括弧内の値に最も近い整数を返します。それが求めるインデックスです。
各時間軸の上限値と下限値、すなわち \(x_{i,m}~~と~~ x_{i,-m}\) は、ひとつ前の時間軸における \(x_{i-1,m}~~と~~ x_{i-1,-m}\) から、上の式を使って、分岐先インデックスを求めれば、自ずと決まります。
以上のロジックから、すべてのノードからの分岐先のノード(座標)が特定でき、各時間軸の最大値、最小値も確定できます。
4.4.5.3.5 遷移確率を変数とする3元連立方程式の特定と、解法
\(x\) の3項ツリーの接続関係が決まったので、次にそれぞれの分岐先への遷移確率を、すべてのノードで求めます。ノード \(x_{i,j}\) から、中心ノードへの遷移確率を \(p_{i,j,mid}\) 上のノードへの遷移確率を \(p_{i,j,up}\) 下のノードへの遷移確率を \(p_{i,j,down}\) と置きます。3項ツリーが、Hull-Whiteモデルを数値的に近似していると言える為には、下記の条件を満たす必要があります。これらの条件を使って、\(p_{i,j, mid},~~p_{i,j, up},~~p_{i,j, down},\) を未知数とする方程式を立て、それを解けば、遷移確率が求まります。すなわち、
- 3項の分岐先への期待値が、Hull-Whiteモデルによる微小時間後の \(M_{i,j}\) と一致する。
- 3項の分岐先への分散が 、Hull-Whiteモデルによる微小時間後の \(Var_{i,j}\) と一致する。
- 3項の分岐先への分岐確率の合計は 1
この様子を図示すると、下記のようになります。
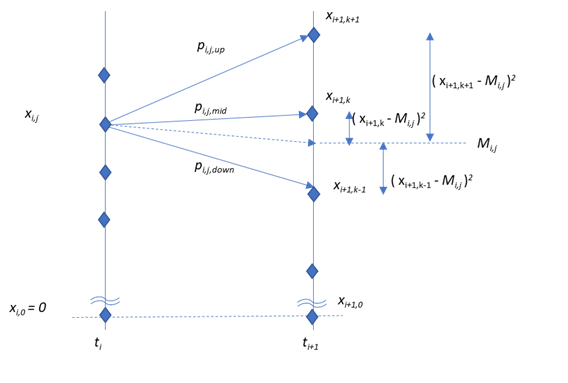
ノード \(x_{i,j}\) から、次のノードへの条件付き期待値 \(M_{i,j}\) と分散 \(Var_{i,j}\) は 4.41, と 4.42 式、あるいは 4.43,と 4.44 式で、すでに求めています。これらを使って、\(p_{i,j,mid},~~p_{i,j,up},~~p_{i,j,down},\) を未知数とする、次の様な3元の連立方程式が立てられます。
\[ \begin{cases} & p_{i,j, mid}+p_{i,j, up}+p_{i,j, down}=1 \\ & p_{i,j, mid}\times x_{i+1,k}+p_{i,j, up}\times x_{i+1,k+1} + p_{i,j, down}\times x_{i+1,k-1} = M_{i,j} \\ & p_{i,j, mid}\times (x_{i+1,k}-M_{i,j})^2+p_{i,j, up}\times (x_{i+1,k+1}-M_{i,j})^2 +p_{i,j, down}\times (x_{i+1,k-1}-M_{i,j})^2=Var_{i,j} \tag{4.46} \end{cases} \]これを解けば、遷移確率が求まります。連立方程式を、\(p_{i,j, mid},~~p_{i,j, up},~~p_{i,j, down},\)について整理すると、下記のようになります。
\[ \begin{cases} & p_{i,j, mid}=\frac 2 3 -\frac{(M_{i,j}~-~x_{i+1,k})^2}{3Var_{i,j}} \\ & p_{i,j, up}=\frac 1 6 +\frac{(M_{i,j}~-~x_{i+1,k})^2}{6Var_{i,j}} +\frac{(M_{i,j}~-~x_{i+1,k})}{2\sqrt 3 Var_{i,j}} \\ & p_{i,j, down}=\frac 1 6 +\frac{(M_{i,j}~-~x_{i+1,k})^2}{6Var_{i,j}}-\frac{(M_{i,j}~-~x_{i+1,k})}{2\sqrt 3 Var_{i,j}} \tag{4.47} \end{cases} \]これをすべてのノードで求めれば、\(x\) の3項ツリーの構造がすべて完成します。\(x_0=0\) をスタート点として、その樹形構造のイメージ図を下記します。
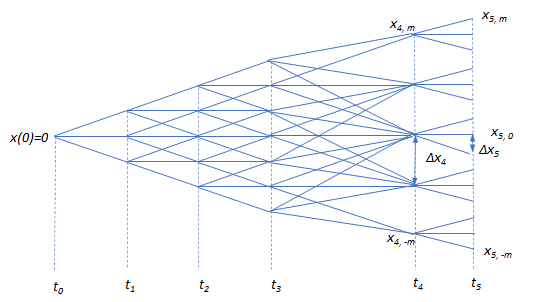
\(t_3~~から~~t_4\) の時間幅が、大きくなっており、その結果 \(t_4\) 軸上の \(Δx_4\) が大きくなっています。時間軸間隔をそのように設定すると、\(t_4\) 軸上の \(x\) のノード数が減り、\(t_3\) からの分岐が集中している様子が見て取れます。また \(t_4~~から~~t_5\) の時間幅は狭くなっており、その結果 \(Δx_5\) は小さくなり、分岐先がきめ細かくなっています。この性格を使って、数値解の収束を良くする為、イベント日の前の時間軸を狭くして、イベント時の分布をより詳細に近似するようなテクニックがあります。