1. QuantLibを使ってみる
1.2 Example を試す
1.2.7 Gaussian1dModels : Gaussian Short Rate Model と Markov Functional Model
1.2.7.1 Gaussian1dModels パート1
1.2.7.1.1 はじめに
既に解説済の、 “CallableBonds” と “BermudanSwaption” の Example コードでは、Short Rate Models の中で、比較的ポピュラーなモデルをいくつか使ってバーミューダ・スワップションの価格評価を行っていました。この Example コードでは、Guassian Short Rate Model(ガウス Short Rate Model、以下“GSR”)と、Markov Functional Model(マルコフ汎関数モデル、以下“MFM”)を使って、通常の金利スワップを対象とするバーミューダ・スワップション、及び CMS スワップを対象とするバーミューダ・スワップションの価格評価を行っています。
また、イールドカーブについては、将来の LIBOR の期待値を導出する為に使われる Forecasting Curve (Forwarding Curve, Index Curve とも呼ばれています)と、それを現在価値に割引く為の Discounting Curve を別にする、マルチカーブ対応にしています。
この Example コードや、ここで使われているクラス群は、最近になって(とは言っても 2014 年頃)開発されたものです。QuantLib では、プロジェクトの開始当初(2000年代前半)に、Short Rate Model クラスのクラス階層が、ほぼ出来上がっていましたが、この Example コードでは、その一部しか使っていません。おそらく、この間に起こった市場の変化(マルチカーブ対応)や、モデルの進化(価格を計算するアルゴリズムについては、新しい方法が色々と発表されています)に合わせる為、当初の骨格では対応しきれなかった為かと思われます。
これまでの Example コードと比べると、ここでテストされている QuantLib の機能は、相当多岐に渡っています。また、クラスの構造もこれまで説明した Short Rate Model とは異なっています。従って、それを全部まとめて解説すると消化不良を起こしそうなので、解説は、3部に分けて行います。
まず、パート1では通常の金利スワップを対象としたバーミューダ・スワップションを、GSR を使った価格エンジンを使って価格評価します。価格評価の前に、GSR モデルのパラメータを、ベンチマークとなるヨーロピアンオプション価格データに Calibration する必要がありますが、ここで使われている Calibration の手順は、"CallableBonds" や "BermudanSwaption" でのCalibrationの手順とは、異なっています。前のセクションでは、 “CalibrationHelperオブジェクト”(ベンチマーク商品の価格計算を行い、SolverにおけるCost関数の役割を果たすオブジェクト)を外生的に生成していました。一方、ここで使われている CalibrationHelper は、価格エンジンに内包している CalibrationHelper の自動生成機能を使って生成されています。
パート2でも、GSR を使って、通常のバーミューダ・スワップションの価格評価を行いますが、ここでは、モデルパラメータを、Out of the Money のヨーロピアンオプション価格に Calibration して価格評価を行います。ここでも、価格エンジンに備わった、CalibrationHelper の自動生成機能を使っています。その自動生成機能のスイッチを変えると、バーミューダ・スワップションのストライクに合わせた CalibrationHelper を自動的に生成してくれます。また、スワップのみなし元本が逓減していく形のバーミューダ・スワップションの Calibration と価格評価も行っています。
パート3では、CMS(Constant Maturity Swap)を対象とするバーミューダ・スワップションを、GSR と MFM を使った価格エンジンを使って価格評価します。CMS は、仮にオプションが付いてなくても価格評価が難しいエキゾチックな商品です。それにオプションが付されると、価格評価はかなり困難です。完全では無いものの、とりあえず GSR と MFM の2種類のモデルで価格評価を試みています。
1.2.7.1.2 Gaussian Short Rate ModelとMarkov Functional Modelについて
コードの解説に入る前に、この Example コードでテストされている、Gaussian Short Rate Model(Hull-Whiteモデル)と Markov Functional Model について簡単に解説したいと思います。いずれも、上級編で、やや詳しく解説しているので、そちらの方もご覧下さい。(Hull White モデル、Markov Functional Model)
Gaussian Short Rate Model(“GSR”)とは、瞬間短期金利の確率過程が、ガウス分布すると仮定した Short Rate Model の総称です。そのようなモデルとしては、1ファクターの Vasicek モデルや、Hull-White モデル、あるいはマルチファクターの Hull-White モデルなどがあります。QuantLib でオブジェクトモデル化された GSR は、1ファクターで、モデルの Volatility パラメータと中心回帰強度パラメータを、それぞれ時間の関数とした Hull-White モデルの事を指しています。数式で表現すると、下記のようになります。
\[ dr(t)=k(t)[θ(t)-r(t)]dt+σ_r (t)dW(t) \tag{1} \]Hull-White は、この確率微分方程式を解いて、ゼロクーポン債価格の解析解と、それを対象としたヨーロピアンオプションの解析解を導出しました。 しかし、QuantLib で実装されている GSR は、ゼロクーポン債価格の解析解を、Hull-White のオリジナルの論文とは異なった方法で求めています。また、Hull-White はバーミューダタイプのオプション価格計算の為に3項Tree アルゴリズムを使いましたが、QuantLib で実装されている数値計算アルゴリズムは、それとは異なります。
GSR では、まず、新たに初期値が 0 でガウス分布する状態変数(確率変数) x(t) とおき、瞬間短期金利 r(t)を、この x(t)と t 時における瞬間フォワード金利の和で表現できると定義します。
\[ r(t)=x(t)+f(t) \tag{2} \]すると、この x(t) の確率過程は、下記式のような確率微分方程式で表現でます。(解析のプロセスは省略しますが、HJM フレームワークを使って解析するとこうなります)
\[ \begin{align} & dx(t) =(y(t)-k(t)x(t))dt+σ_r (t)dW(t),~~~~~ x(0)=0 \\ & ~~where~~~ y(t)=\int_0^t e^{-2\int_u^t k(s)ds} σ_r (u)^2 du \tag{3} \end{align} \]ここからさらに解析を進めていくと(やはり解析のプロセスは省略し結果だけ示します)、将来のゼロクーポン債価格(すなわちイールドカーブ)が、Tフォワード測度の下で、下記式のように求まります。
\[ \begin{align} & P(t,T)=\frac{P(0,T)}{P(0,t)} exp \left[-x(t)G(t,T)-\frac 1 2 y(t)G(t,T)^2 \right] \\ & ~ where~~~ G(t,T)=\int_t^T e^{-∫_t^u a(s)ds}du \tag{4} \end{align} \]注目点は、このゼロクーポン債価格式は、ガウス分布する x(t) の汎関数となっている所です。
さらに、時点 ω における x の値が x(ω) であった場合の、 t 時(但し ω < t )における x(t) の条件付き期待値と条件付き分散も下記式のように求まります。(これも、解析のプロセスは省略し、結果のみ示します。)
\[ E \left[ x(t) | x(ω)\right] = A(ω,t)~x(ω)+\int_ω^t A(s,t)\left(y(s)-σ_r (s)^2 G(s,t)\right) ds \tag{5} \] \[ \begin{align} & Var \left[x(t)|x(ω)\right]=\int_ω^t A(s,t)^2 σ_r (s)^2 ds ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ \\ & ~where~~~ A(s,t)=e^{∫_s^t -k(u)du} \tag{6} \end{align} \]以上の (4),(5),(6)式により、将来のゼロクーポン債価格が拡散していく様子、すなわち特定の時点のゼロクーポン債価格(イールドカーブ)を、ガウス分布する状態変数 x(t) から直接求める事ができます。Hull-White のオリジナルの論文では、r(t) の拡散する様子を表現し、そこからゼロクーポン債価格を求めていました。また、3項 Tree を構築する際、ガウス分布する x(t) の Tree をまず構築し、それを r(t) の Tree に換算して、r(t) の拡散過程を Tree で表現していました。しかし、上記のようにゼロクーポン債価格を x(t) の関数として直接導出しておけば、3項 Tree よりも計算効率の良いアルゴリズムで、ゼロクーポン債価格が導出できます。
解析の詳細なプロセスや、アルゴリズムについては、この Example コードの開発者である P. Caspers 氏の論文“One Factor GSR あるいは、Andersen-Piterbargの"Interest Rate Modeling" の Volume II Section 10.1.2.2 をご覧ください。
そして、Markov Functional Model(MFM) と GSR は、モデルの発想は全く異なるものの、ガウス分布する状態変数 x(t) の汎関数としてゼロクーポン債価格を求めている点では一致しています。但し MFM では、その関数形は GSR のように、モデルを解析して求めるのではなく、ベンチマークとなるヨーロピアンオプションの市場価格から、Bootstrapping-Interpolation 法と似たようなアルゴリズムで求めています。また GSR でも MFM でも、x(t) がガウス分布すると仮定しているので、その遷移確率が解析的に求まり、その遷移確率を使ってゼロクーポン債価格の期待値が比較的簡単に計算できます。その結果、GSR と MFM は、ゼロクーポン債価格の汎関数を求めるアプローチは大きく異なるものの、最終的に同じアルゴリズム(正規分布の遷移確率密度関数を使った、ガウス・エルミート求積法)で、ゼロクーポン債価格の期待値を求めています。QuantLib では、GSR も MFM も、同じベースクラスとなる Gaussian1dModel クラスから派生して定義・実装されているのは、その為かと思われます。
1.2.7.1.3 プロジェクトのビルドと実行
これまで通り、ソースコードのビルドの方法から説明します。QuantLib のインストール方法を解説したセクションですでにビルドしていれば、再ビルドは必要ありません。もし、ビルドが済んでいない場合は、次の手順で、Debug モードでビルドし、試しに実行してみて下さい。
- QuantLib のファイル Folder の Example ディレクトリから、Gaussian1DModels のディレクトリを探し、そこにあるプロジェクトファイル Gaussian1DModels.vcxproj をダブルクリックし開ける。Visual Studio が起動され、このプロジェクトファイルが開かれる。
- ソリューションエクスプローラーに表示されているプロジェクトファイルのディレクトリを展開し、SourceFiles のフォルダーにある Gaussian1DModels.cpp をクリックする。約 680 行あるソースコードが開かれる。
- きちんと動作するか、まず確認してみる。メニューバーからビルド→ソリューションのビルドを選択。ビルドが開始される。
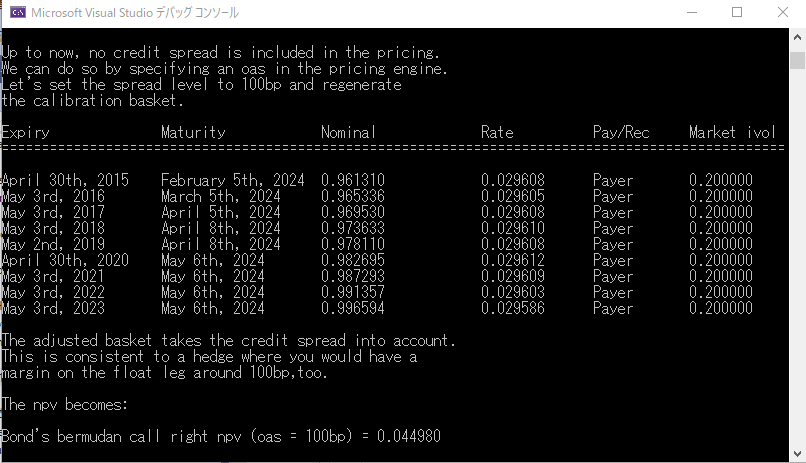
- ビルドが正常終了すれば、試しにプログラムを走らせてみる。メニューバーから “デバック” → “デバックの開始” を選択。下記のコンソール画面が出力されれば成功。(但し、プログラムが終了すると同時に Console 画面も消えてしまうようであれば、メニューバーから、“ツール” → “オプション” → “デバック” → “全般” を選択し、「デバックの停止時に自動的にコンソールを閉じる」のチェックボックスをはずします。)
1.2.7.1.4 Gaussian1DModelsのソースコードの解析:全体の概要
では、ここからソースコードを解析していきます。Gaussian1dModels.cpp のファイルを、Visual Studio で開くか、面倒であれば、こちら"Gaussian1DModelsCpp.html"を開いてください。
この Example コードは、全体で、約 680 行ありますが、これまでの Example コードと同様、価格評価の対象となる商品オブジェクトと、価格計算のアルゴリズムを持つ価格エンジンオブジェクトを、それぞれ部品から作成し、組み立て、価格計算を行っています。但し、価格計算の前に、いくつかの方法で、モデルパラメータの Calibration を行っています。 この Example では、これまでの Example に比べ、コンソール画面の出力に、比較的丁寧な解説が出力されているので、まずコンソール画面の出力をよくご覧下さい。この Example で何をテストしようとしているかが、分かると思います。
ここでは
- Guassian Short Rate Mode(ガウスShort Rate Model ”GSR”;具体的には1ファクターの Hull-White モデルで、モデルパラメータを時間の関数としたもの)と、
- Markov Functional Model(1ファクターのマルコフ汎関数モデル”MFM”)
を使って、金利スワップ対象のバーミューダ・スワップションと、CMS(Constant Maturity Swap)対象のバーミューダ・スワップションの価格評価を行っています。
また、価格評価の前にモデルパラメータの Calibration が必要になりますが、この Example コードで使われている価格エンジンは、CalibrationHelper を、何通りかの方法で、自動生成する機能を持っており、それぞれの方法をテストしています。具体的には、
- At the Money のヨーロピアンスワップションに Calibration する方法、
- 対象となるバーミューダ・スワップションのストライクに合わせて Calibration する方法。
- 変則的なキャッシュフローを持つスワップションに対応する Calibration 方法、をテストしています。
また、Example コードの後半部分では、CMSを対象とするバーミューダ・スワップションの価格評価を、GSR とMFM を使った価格エンジンで行っています。
1.2.7.1.5 Gaussian1DModelsのソースコードの解析:詳細
(1) 事前準備①: ローカルメソッド
main()関数は 131 行目からスタートしますが、その前に、この Example 専用のメソッドが2つ用意されています。
ひとつめは、61 行目の printBasket() です。このメソッドは、引数として取った CalibrationHelper の配列から、Calibration 対象となったヨーロピアンスワップションの内容(行使日、対象スワップの満期日、みなし元本、ATM ストライクレート、Black Implied Volatilityなど)を取り出し、それをコンソール画面に出力する関数です(上記のコンソール画面出力で確認して下さい)。配列の要素である CalibrationHelper オブジェクトは、モデルパラメータを Calibration する目的で作られたオブジェクトで、
・ ヨーロピアンスワップションの商品属性を保持する事と、
・ それの価格計算機能(Blackの公式を使った場合と、Short Rate Model を使った場合)
を提供しています。すなわち Instrument オブジェクトと PricingEngine オブジェクトを合体させた機能を持っています。CalibrationHelper については、既に BermudanSwaption の Example の所で、簡単に説明しました。
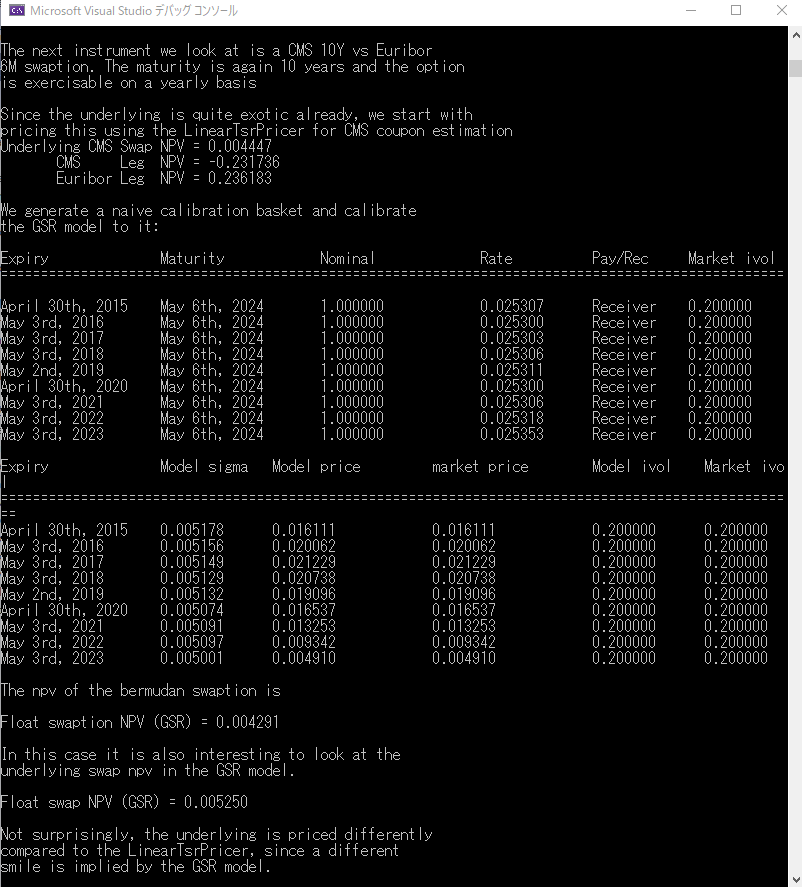
ふたつめは、95 行目にある printModelCalibration()です。このメソッドは、Calibration の結果をコンソール画面に出力するメソッドです。出力内容は、Calibration された
・ モデルの Volatility パラメータ σ(t) の値、
・ モデルによるヨーロピアンスワップションの価格、
・ Black の公式で計算されたヨーロピアンスワップション価格、
・ モデル価格によるBlack Implied Volatility、
・ 市場データのBlack Implied Volatility
です。
では、main()の本体に進みます。
(2) 事前準備② : 例外処理
main( ) 関数全体を try{ } で囲み、関数内でエラーが発生した場合、677 行目の例外処理に飛びます。これまでの Example は、標準ライブラリーで準備した例外処理だけでしたが、ここでは、QuantLib が用意した例外処理にも飛ぶようになっています。677 行目に
catch (const QuantLib::Error & e) { … } とあり、QuantLib が定義した例外処理にひっかかった場合、ここに飛ぶようになっています。QuantLib では、独自の例外処理(Error Handling)を定義しており、ライブラリーの至る所で使われています。
QuantLibにある例外処理機能は、Luigi Ballabio 氏の “Implementing QuantLib” の Appendix をご覧下さい。このサイトにもその訳 Appendix A.6.2 を載せています。
事前準備③:価格評価基準日の設定
141 行目で時価評価日を 2014 年 4月30日 に設定しています。おそらくこの Example が作成された頃の日付けだと思いますが、これまでの Example と比べると、比較的新しいです。実際に、ここで使われている Guassian Short Rate モデルや価格エンジンは、QuantLibライブラリーの中では比較的最近作られたクラスのようです。
(3) 商品オブジェクトの生成
まず価格評価の対象となる商品オブジェクトを生成します。ここでは、金利スワップを対象としたバーミューダ・スワップションです。これまで通り、その部品から作っていきます。
(3)-1 イールドカーブオブジェクトの生成
部品の中でも最も重要な部品であるイールドカーブを生成します。147~167 行目にある通り、その生成手順もこれまでと、ほぼ同じです。まず、金利の市場データから、Quote オブジェクトを作成し、次にそれを Handle オブジェクトに保持させ、さらにそれを使ってイールドカーブ(TermStructure クラスのインスタンス)の Handle オブジェクトを生成しています。ここでは、マルチカーブ対応する為に、forecasting curve(154行目の yts6m)と discounting curve(156 行目の ytsOis)の2種類生成しています。(但しテスト用なので、シンプルに全期間一定と置いたフラットイールドカーブです。) イールドカーブが出来たので、159 行目で、これを使って、6カ月 Euribor インデックスを生成しています。
(3)-2 スワップション Volatility Cube データを生成
次に 169~173 行目で SwaptionVolatilityStructure オブジェクトを生成しています。この Volatility の期間構造は、市場で取引されている Swaption の Black Volatility キューブ(オプション期間 × 対象スワップ期間 × ストライクの 3 次元のデータ)に相当し、このデータに対し、モデルの Volatility パラメータが Calibration されます。従って、このデータは商品オブジェクトの部品ではなく、CalibrationHelper の部品になります。SwaptionVolatilityStructure クラスは、その 3次元データをオブジェクトモデル化したものですが、ここでは対象スワップ期間やストライクに関係なく、すべてのオプション行使期間軸、対象スワップ期間軸、ストライク軸で 20%(Black Volatility です)のフラットなキューブを想定しています。ここでもイールドカーブと同様、原データを Quote オブジェクトに持たせ、それをさらに Handle オブジェクトに持たせ、さらにそれを SwaptionVolatilityStructure オブジェクトの Handle に持たせるという手順で作成されています。このようなデータ構造を取る理由は、既に他の Example コードで既に説明しました。
(3)-3 バーミューダ・スワップションの生成
179~208行目で、バーミューダ・スワップションを生成しています。
その為に、ます対象スワップから生成します。ここでは、固定金利 4% の Payer スワップで、1 年後スタートの 9 年物スワップ(即ち、時価評価日からスワップの満期まで 10 年)を生成しています。これも、部品から順番に組み立てています。スワップ(商品)オブジェクトの生成方法については、MulticurveBootstrapping の所で説明したので、そちらをご覧下さい。ここでは、商品オブジェクトとして、NonStandardSwap クラスのオブジェクトを生成しています。これは、みなし元本を逓減させていく商品など、キャッシュフローがやや複雑なスワップにも対応出来るクラスで、後ほど、価格評価の例で登場します。
次に、この対象スワップを使って、バーミューダ・スワップションのオブジェクトを生成します。その部品として、200~206 行目でバーミューダ・スワップションの行使日の配列を生成しています。BermudanExercise へのスマートポインターがそれです。この行使日の配列と、対象スワップを組み合わせて、バーミューダ・スワップションのオブジェクトを生成しています。207 行目にある通り、NonStandardSwaption クラスのコンストラクターに、対象スワップと行使日を渡し、完成です。
(4) モデルと価格エンジンの生成、およびモデルパラメータの Calibration (1)
(4-1) GSR モデルの生成
商品オブジェクトが完成したので、次は、価格エンジンの生成です。ここでは GSR モデルを使った価格エンジンを生成するので、まず GSR モデルオブジェクトを生成し、それを価格エンジンに組み込みます。但し、価格エンジンを使う前に、まずモデルのパラメータを市場データに Calibration する必要があります。この Example では何通りかの方法で Calibration を行っており、それぞれ順番に説明しますが、とりあえずここでは最初のCalibration方法を Calibration(1) とします。
Calibration の対象となるパラメータは、(1)式にある Volatility パラメータ σ(t) と中心回帰強度パラメータ k(t) です。まず、Volatility パラメータ σ(t) ですが、階段関数の形をした(Piecewise Constantな)関数と仮定しています。214~217 行目で、σ(t) の時間軸となる配列と、そこに入る σ(t) の値(初期値としてすべて1%に設定)の配列を生成しています。一方、中心回帰強度パラメータ k(t) については定数と仮定し、無理やり外生的に与えています(217行目で0.01に設定)。このパラメータの Calibration は相当ややこしく、場合によっては、別のハイスペックなモデルでの価格計算が必要になります。手間をかけた割に、中心回帰強度パラメータの役割の一部は、Piecewise Constantな σ(t) でも果たせるので、実務でも適当な値を外生的に与えるのが一般的だと思います。
そして、それらを引数として、230 行目で GSR モデルを生成しています。コンストラクターに、σ(t)、k(t) 以外に、6カ月 Euribor の Forecasting Curve(インデックスカーブ)を渡していますが、これを使って、モデルオブジェクト内で、中心回帰レベルパラメータ θ(t) が自動的に Calibration されます。これで、GSR モデルが作成されました。
(4)-2 価格エンジンの組み立て
モデルが出来たので、これを使って価格エンジンを組み立てます。233 と 236 行目で、このモデルをベースにした2種類の価格エンジンを作っています。一つ目の Gaussian1dSwaptionEngine は、ヨーロピアンスワップション用の価格エンジンで、もう 1 つの nonstandardSwaptionEngine は、バーミューダ・スワップション用の価格エンジンです。いずれも、前の “BermudanSwaption” の Example コードで価格計算に使われた Hull-White モデル用の価格エンジンとは異なります。これらのエンジンは、QuantLib の中でも比較的最近になって加えられたもので、これまでの Short Rate Model 用のエンジンとは異なった機能を持っています。その機能については、後ほど説明します。
また、ゼロクーポン債価格を計算するアルゴリズムも、従来の Hull-White モデルベースの価格エンジンとは異なります。GSR をベースにしたこの価格エンジンは、冒頭で述べた通り、瞬間短期金利 r(t) からではなく、ガウス分布する状態変数 x(t) から直接ゼロクーポン債価格を求めます。その方法は、まず (4)式の通り、ゼロクーポン債価格が x(t) の汎関数で求まっています。また(5)式から x(t) の条件付き期待値と分散も分っています。さらに、 x はガウス分布するマルコフ過程という前提なので、遷移密度関数が解析的に求まっています。これらの式から、ガウス・エルミート求積法を使って、ゼロクーポン債価格の期待値を数値的に求める事が出来ます。234 行目にある価格エンジンのコンストラクターに渡している引数で、64 は、数値積分で使われる求積ポイントの数で、7.0 は、x(t)の範囲を、±7.0標準偏差の範囲内で状態変数軸を設定する事を意味しています。この方法は、Hull-White が提示した3項Tree による数値計算よりも高速です。
価格エンジンの部品となるイールドカーブは、discounting curve として使われる OIS カーブになっている事に注意して下さい。GSR モデルが想定する金利の確率過程は、6カ月 Euribor カーブ(から導出される瞬間フォワード金利のカーブ)に中心回帰すると想定され、それを基にフォワード金利が計算されるのに対し、それを現在価値に割引くには、OIS カーブを使うという事です。
(4)-3 Calibration (1)
価格エンジンが完成したので、240 行目で、それを作成済みの swaption オブジェクトに設定しています。そして、その直後のコメントをご覧下さい。その内容は上記のコンソール画面にも出力されています。
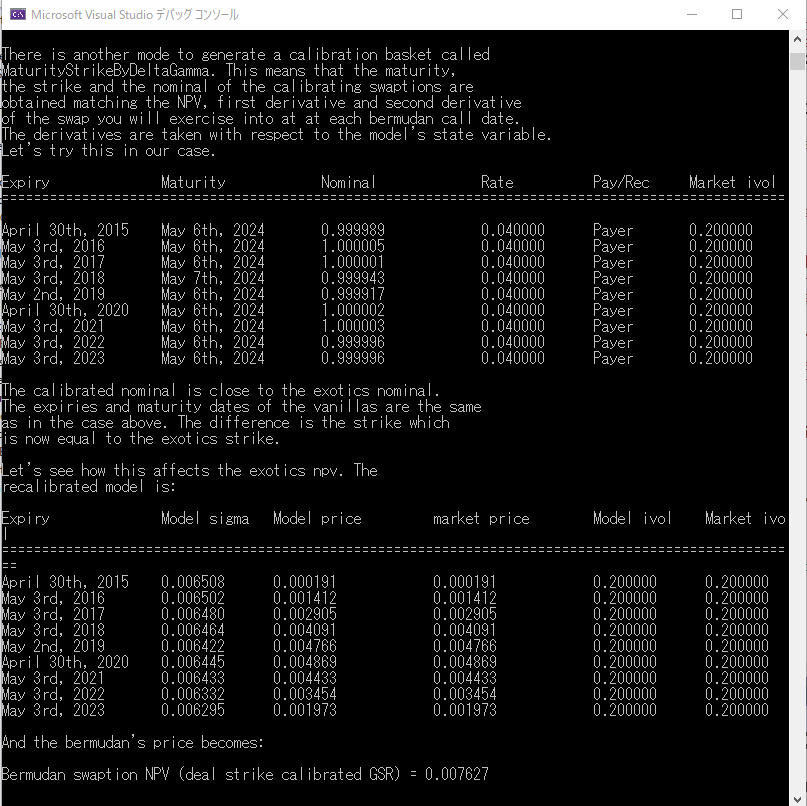
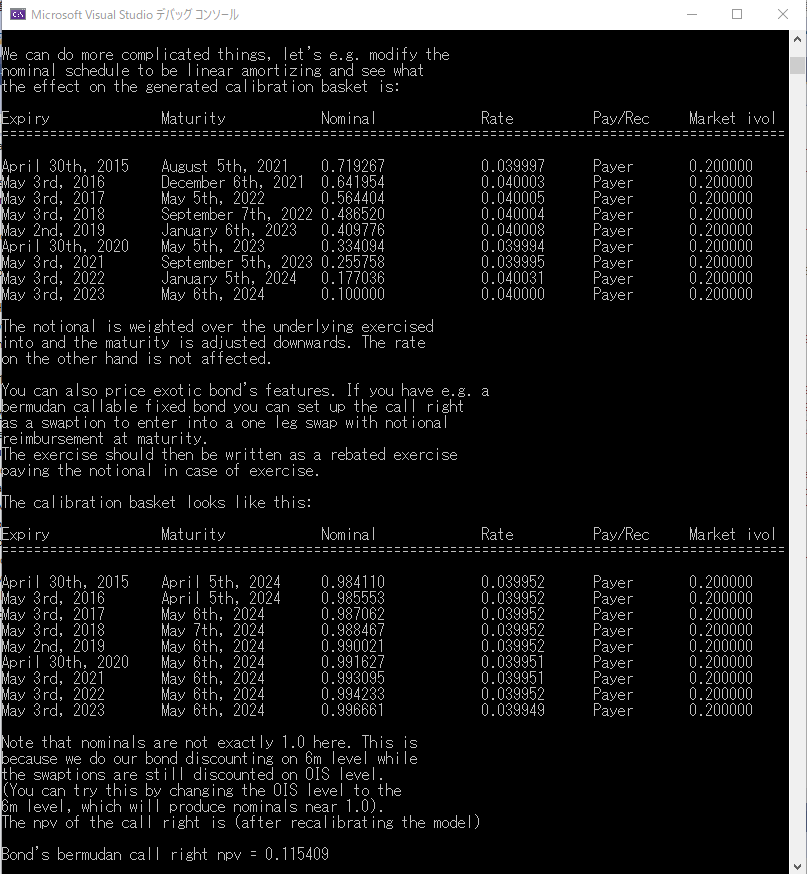
“The engine can generate a calibration basket in two modes. The first one is called Naive and generates ATM swaptions adapted to the exercise dates of the swaption and its maturity date."
「この価格エンジンは、内部で、CalibrationHelper のバスケットを、2通りの方法で生成する事が出来ます。ひとつは、Naïve と呼ばれる方法で、各行使日と対象スワップ期間において、At the Money となるスワップション用です。」
先ほど述べた、価格エンジンの新たな機能のひとつがこれです。 前の“BermudanSwaption”の Example コードでは、CalibrationHelper を、モデルの外で構築していました。ところが、この価格エンジンは、それを自動的にエンジン内部で行ってくれるというものです。この機能を使って、255 行目で、CalibrationHelperオブジェクトの配列が生成されました。
(注: コメントでは、価格エンジンによって CalibrationHelper オブジェクトが生成されると述べていますが、この後の 255~256 行目をみると、swaption(商品インスタンス)から calibrationBasket( )メソッドが呼び出され、CalibrationHelper が生成されています。一見すると、商品オブジェクトが CalibrationHelper のバスケットを生成しているように見えます。しかし、このメソッドは、背後で、さらに価格エンジン(Gaussian1DNonstandardSwaptionEngine)が持つ calibrationBasket()メソッドを呼び出しており、実際のアルゴリズムは、このエンジンのベースクラスである BasketGeneratingEngine で実装されています。しかし、QuantLib の Reference Manual の中では BasketGeneratingEngine について、何の説明もされていません。もしかしたら、まだ開発途上かもしれません)
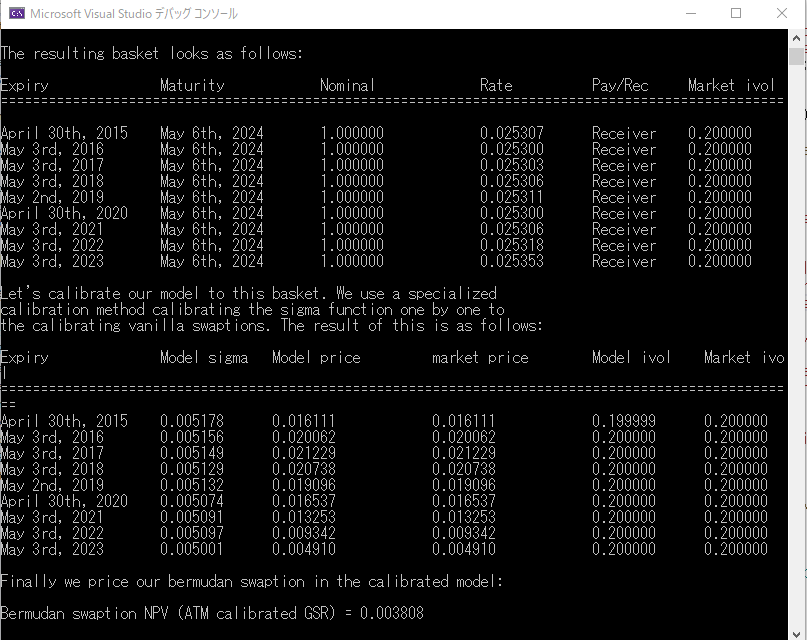
258 行目で、この Example コード用のローカル関数 printBasket() を使って、その内容をコンソール画面に出力しています。出力されているのは、Calibration 対象となる、At the Money のヨーロピアン・スワップションのリストです。行使日は、それぞれバーミューダン・スワップションの行使日に対応しており、対象スワップの満期日は、すべて同じ May 6th 2024 となっています。いわゆる Co-terminal Swaption の集合です。
CalibrationHelper が生成されたので、いよいよ Volatility パラメータの Calibration を行います。まず 269 行目で、たった今生成された CalibrationHelper に、ヨーロピアンスワップション用の価格エンジンを設定します。先ほど生成した2つの価格エンジンの内、Gaussian1dSwaptionEngine クラスのインスタンスである swaptionEngine がそれです。次に、272 と 273 行目で、多変数用の Solver と、Solver の収束条件を設定します。Solver は QuantLib が用意している Levenberg-Marqaurdt 法を使ったオブジェクトを生成しています。そして、277 行目で、モデルオブジェクト(gsr)から calibrateVolatilitiesIterative( )メソッドを呼び出せば、Calibration アルゴリズムが実行されます。
(注意: 初期の Short Rate Model クラスでは、Calibration のアルゴリズムを、ベースクラスである CalibratedModel クラスで calibrate( )メソッドを実装し、すべての Short Rate Model 派生クラスで使う事を想定していたと思われます。前の BermudanSwaption の例ではそうでした。しかしこの GSR モデルでは、独自の Calibration のアルゴリズムを実装しており、この Example コードでもそれが使われています。Short Rate Model のオブジェクトライブラリーは、QuantLib プロジェクトの初期段階(2000年代前半)で、ある程度出来上がっており、その後、そのライブラリーでは対応できない Calibration の方法を、このクラスで新たに付け足したものと思われます。)
これで、GSR モデルのパラメータが市場データに Calibration されました。結果は、上記のコンソール画面の出力の通りです。GSR モデルによる計算結果と市場価格が完全に一致しています。従って、当然ながら GSR モデルで計算された価格に内容する Implied Black Volatility も、市場の Implied Black Volatility と完全に一致しています。ここでは、フィットさせる対象のヨーロピアン・スワップションの数と、Calibration される Volatility パラメータの数が同じになっているので、こういう結果になります。こういうのは、個人的には、モデルがオーバーフィットされ、パラメータが不安定になるので、必ずしも好ましいとは思いませんが。
(5) バーミューダン・スワップションの価格計算
モデルのパラメータが求まったので、本来の目的であるバーミューダン・スワップションの価格計算を行います。既にバーミューダン・スワップションの商品オブジェクトと価格エンジンは設定済です。後は、287 行目の swaption -> NPV( ) を呼び出すだけです。
290 行目で、計算結果をコンソール画面に出力しています。上記のコンソール画面の出力をご覧下さい。価格は 0.003808(38.08bp) でした。QuantLib の古いバージョンでの Example コードでは、計算時間も出力するようになっていましたが、最新のバージョンでは取り除かれたようです。ちなみに計算時間は 約 5秒かかっていました。使った価格エンジンは、数値解を求めるアルゴリズムを使っているので、一瞬で計算という訳にはいきません。
長くなったので、一旦ここでストップします。ここまでを簡単に振り返ると、これまでの Example コード同様、QuantLib を使って金融商品の価格を計算するには、
- 価格評価の対象となる金融商品オブジェクト(Instrumentクラスのオブジェクト)と、
- 価格計算アルゴリズムをカプセル化した価格エンジンオブジェクト(PricingEngineクラスのオブジェクト)を、
それぞれ部品から組み立て、 - 最後に、商品オブジェクトに価格エンジンを設定し、NPV()メソッドを呼び出すだけです。
ただ、部品の組み立てが結構複雑で解りにくにので、それを様々な Example で慣れていくようにすればいいでしょう。特に、この Example では価格エンジンの根幹部品であるモデルオブジェクトの、Volatility パラメータの Calibration 方法のテストに重点が置かれています。この Example では、別のパラメータ Calibration 方法もテストしていますので、次回はそこから解説をします。
<ライセンス表示>
QuantLibのソースコードを使う場合は、ライセンス表示とDisclaimerの表示が義務付けられているので、添付します。 ライセンス