上級編 6. Libor Market Model
6.6 モンテカルロシミュレーション
6.6.3 乱数の生成方法
6.6.3.3.4 ソボル列
冒頭で述べた通り、超立方体内で一様分布(に近い)点列を生成する場合、ベクトルの各要素を、すべて同じ基底を使った van del Corput 数列で生成してしまうと、各次元軸に平行な格子状の点列が生成される事になります。すると、各次元への射影された点の多くが重なってしまい、解像度が低くなってしまいます。その解決方法のひとつは、各次元で使う基底 b を、それぞれ別個の素数にする事です。すると次元ごとの点の間隔がそれぞれ異なり、各次元への射影が殆ど重ならず、解像度が上がります。実際、そのようにして生成される高次元の点列は、Halton によって示されており、その点列は ハルトン列(Halton sequence)と呼ばれています。その説明は省略しますが、ハルトン列は、b を大きく取った次元の点が偏ってしまうという欠点があり、次元があまり大きくない場合でしか使えません。(偏りを無くすには、次元ごとに決めた基底の最小公倍数の、さらにそのべき乗のサンプル数が必要になり、その総数は巨大になってしまいます。)
射影が重ならないようにする為の別の工夫として、点ベクトルの座標を、次元ごとにずらして生成する方法があります。ある整数 k を、基底 b を使って冪級数展開し、その係数を次元の高い順番に並べれば、k の b 進数表記になります。それをベクトルと看做して、それに行列を作用させると(ベクトルを回転かつ伸縮させる操作に相当)、別の b 進数表記された数になります。それを d 個用意すれば、d次元の点ベクトルが生成できます。この時、基底となる b を d よりも大きい素数を使って点ベクトルを生成するアルゴリズムが Faure によって提示されており、その点列をフォーレ列(Faure sequence)と呼びます。並び替えの際、工夫が必要ですが、詳細の説明は省略します。
また、別の方法として、整数 k を 2 で冪級数展開し、その係数ベクトルに、特定の条件を満たす行列 V を作用させて別の 2進数を生成する方法があります。V を d 個用意すれば、整数 k に対応する 2進数が d 個生成でき、それを d 次元点ベクトルの各要素とする方法が、Sobol によって提示されています。そのようにして生成された点列をソボル列(Sobol Sequence)と呼びます。ソボル列は、比較的高次元でも偏りが少ない点列が生成でき、かつ b=2 とすることでコンピューターのビット演算が高速に行えることから、QMCS では広く使われています。以下にその生成方法を簡単に解説します。
6.6.3.3.5 ソボル列の生成方法
ソボル列は、基底 b を 2 としたファンデルコルプト数列をもとにして生成される、d次元の点列になります。ファンデルコルプト数列は、非負の整数 k を b のべき乗で展開しますが、b=2 として各項の係数を高次の項から順番に並べると、k の 2進数表記になるのでした。Sobolは、その係数ベクトルに、特別な方法で求めたGenerator Matrix(生成行列)と呼ばれる行列 V を作用させる事で、新たな係数ベクトル、すなわち 2進数表記の数を生成します。さらに、その 2進数をファンデルコルプト数列で使った変換関数 \(\psi_2(・)\) で、\([0,1)\) 間の少数に変換します。d次元の点ベクトルを生成するには、生成行列 V を d個用意すれば、整数 k に対応する d個の要素が生成でき、点ベクトルの座標になります。そうやって k=1,2,...,と順番に生成された d次元の点列は、\([0,1)^d \) の超立方体の内部で、Low Discrepancy な点列となります。この方法のポイントは、生成行列 V をどうやって決めるかですが、Sobol は、特定の条件を満たす原始多項式の係数ベクトルを使って V 決める方法を提示しています。
もう少し具体的に説明します。まず非負の整数 k を、2 のべき乗の線形結合で表現します。この時、r-1 をべき乗の最大次数とします。すなわち、
\[ k=\sum_{j=0}^{r-1} a_j(k)~b^j=a_0(k)×2^0+a_1(k)×2^1+⋯a_{r-1}(k)2^{r-1} \]この式の右辺の係数ベクトルを a(k)=\(\{ a_0(k),a_1(k),…,a_{r-1}(k)\} \) と置きます。項数は r 個あるので、r 次のベクトルになります。
ここで、\(r \times r\) 次の Generator Matrix(生成行列) \(\bf {V^{(i)}},~~i=1,2,…,d\) を d個用意し、これを係数ベクトル a(k) に作用させます。但し、最後に mod 2の操作を入れます。(生成行列 \(\bf V^{(i)}\) は上三角行列で、対角成分はすべて 1 になります。\(\bf V^{(i)}\) の決め方は、後で説明します)
\[ \mathbf {V^{(i)}∙a(k)} = \begin{bmatrix} v_1 & ⋯ & v_{1,r} \\ ⋮&⋱&⋮ \\ v_{r,1}&⋯& v_{r,r} \end{bmatrix} \cdot \begin{bmatrix} a_0(k) \\⋮ \\ a_{r-1}(k) \end{bmatrix}~ mod~2 =\begin{bmatrix} y_1^{(i)}(k) \\⋮ \\ y_r^{(i)}(k) \end{bmatrix}=y^{(i)} (k),~~~~~i=1,…,d \]mod 2 の操作は、2 で割った時の余りを返す演算になります。従って、行列演算中のすべての和は 2進数のビット和を行う操作になります。ビット和演算子を ⊕ と表記すると、下記のような値を返す演算になります。これは、コンピューターの論理回路における XOR の操作と同じです。
\[ 0⊕0=0,~~~0⊕1=1,~~~1⊕0=1,~~~1⊕1=0, \]このようにして生成された新たな d 個のベクトル \(y^{(i)}(k),~~~i=1,…,d\) を \([0,1)\) 間の小数点に変換する関数 \(\psi_2(k) \) に代入します。
\[ \psi_2(\mathbf {y^{(i)}(k)})=\sum_{j=1}^r \frac {y_j^{(i)}(k)}{2^j},~~~~~ i=1,…,d \]これで、整数kに対応する d 次元の点ベクトルが生成できました。これを、\(k=0,1,…,2^r\) で行えば、\(2^r\) 個の d次元点ベクトルとなるソボル列が生成されます。
さて、生成行列 \(\mathbf V^{(i)}\) の決め方です。以下に、そのアルゴリズムを説明しますが、なぜそのアルゴリズムでうまくいくのか、私に説明できる能力はありません。数論の深い理解が必要だと思われますが、理解を深めたいと思われる方は、Sobol の論文
“Distribution of points in a cube and approximate evaluation of integrals”(1967)
“Uniformly distributed sequences with an additional uniform property”(1976)
などにあたって下さい。ここでの説明は、実務で使う側にとっての必要最低限の説明に留めます。
生成行列 \(\mathbf V^{(i)}\) は、対角成分がすべて 1 の上三角行列で、その他の上三角の要素は 0 か 1 の値を取ります。ここで \(V^{(i)}\) の縦ベクトルを \(\mathbf v_j^{(i)},~~~j=1,…,r\) と表記します。この縦ベクトルは、方向ベクトル(direction vector)あるいは方向数(direction number)と呼ばれています。行列をベクトルに作用させるのは、ベクトルを各縦ベクトルの方向に回転させる意味があるので、こう呼ばれているのかと思います。この方向ベクトルを以下の方法で生成します。
- 方向ベクトルの初期値として、r より少ない数の 2 進数 \( m_1,…,m_s\) を用意します。但し、それらは \(m_1 \lt2^1,~~ m_2 \lt 2^2,…,m_s \lt 2^s\) となる任意の奇数とする(2進数なので最後の 1桁が必ず 1 となる)。そしてそれらを、\(\frac {m_1}{2^1},~~\frac {m_2}{2^2},…,\frac {m_s}{2^s}\) のように 2 のべき乗で割って \([0,1)\) 間の 2進数表記の少数に変換します。その小数点以下 r 桁までの各桁をベクトルと看做し、それを方向ベクトルの初期値とします。 例えば、\(m_1=1,~~m_2=3,~~m_3=3\) とすると、それらの 2進数表記は 1, 11, 11 となり、それぞれ \(2^1,~~2^2,~~2^3\) で割ってその小数点以下を r=5 桁まで 2進数表記すれば、10000, 11000, 01100 となります。
- 次に、初期値で与えられた \(m_1,…,m_s\) から再帰式を使って \(m_{s+1},~~m_{s+2},…\) を求めます。その再帰式は、2進数の原始多項式で、次の条件を満たすものから導出します。
- 因数分解できない
- 原始多項式の次数を q とすると、その原始多項式で割り切れる多項式 \(x^p +1\) の最小次数が p=2q-1 であること
- 次数 q が、任意の初期値の数 s と同じであること
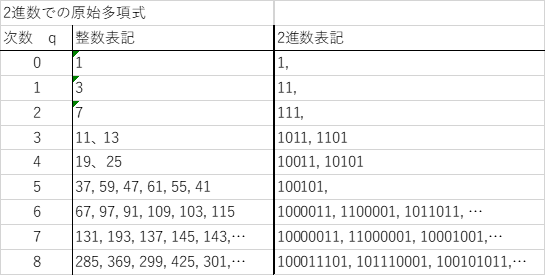
この表では、q の次数に対応した原始多項式の整数表記と 2進数表記を示していますが、 2 進数表記は、原始多項式の係数ベクトル\(\{c_0,c_1,…,c_q\}\) になります。 - この原始多項式の係数ベクトルから、次のような再帰式が導出できます。但し、⊕ は 2 進数表記した数の各桁のビット和(繰り上げ無し)の演算子です。
\[ m_j=2^1~c_1~m_{j-1} ⊕ 2^2~c_2~m_{j-2} ⊕ … ⊕ 2^{q-1}~c_{q-1} m_{j-q+1} ⊕ 2^q~c_q~ m_{j-q} ⊕ 2^0~c_0~m_{j-q} \]
(申し訳ありませんが、なぜこのような再帰式が導出できるのか、私は理解できておらず、説明する能力を持ち合わせていません。 従って、Paul Glasserman本の内容を、ほぼそのまま伝えさせていただきます。)
この再帰式を使って、初期値 \(m_1,…,m_s\) 以降の \(m_{s+1},~~m_{s+2},…\) を求めます。例えば、原始多項式として \(x^3+x^2+1\) を使った場合、その係数ベクトルの要素は、 \(c_0=1,c_1=1,c_2=0,c_3=1\) となります。初期値として \(m_1=1,~~m_2=3,~~m_3=3\) を与えたとすると、 \[ \begin{align} m_4 & =2^1~c_1~m_3 ⊕ 2^2~c_2~m_2 ⊕ 2^3~c_3~m_1 ⊕ 2^0~c_0~m_1 \\ & =2\times 1 \times 3 ⊕ 4 \times 0 \times 3 ⊕ 8\times 1 \times 3 ⊕ 1 \times 1 \times 1= 6 ⊕ 0 ⊕ 24 ⊕ 1 \\ & = \begin {bmatrix} 0 \\1 \\ 1 \\0 \end{bmatrix} ⊕ \begin {bmatrix} 0 \\0 \\ 0 \\0 \end{bmatrix} ⊕ \begin {bmatrix} 1 \\0 \\ 0 \\0 \end{bmatrix} ⊕ \begin {bmatrix} 0 \\0 \\ 0 \\ 1 \end{bmatrix} = \begin {bmatrix} 1 \\ 1 \\ 1 \\ 1 \end{bmatrix} (=15) \end{align} \] \[ \begin{align} m_5 & =2^1~c_1~m_4 ⊕ 2^2~c_2~m_3 ⊕ 2^3~c_3~m_2 ⊕ 2^0~c_0~m_2 \\ & =2 \times 1 \times 15 ⊕ 4 \times 0 \times 3 ⊕ 8 \times 1 \times 3 ⊕ 1 \times 1 \times 3= 30 ⊕ 0 ⊕ 24 ⊕ 3 \\ & = \begin {bmatrix} 1 \\ 1 \\ 1 \\ 1 \\ 0 \end{bmatrix} ⊕ \begin {bmatrix} 0\\0\\0\\0\\0 \end{bmatrix} ⊕ \begin {bmatrix} 1\\1\\0\\0\\0 \end{bmatrix} ⊕ \begin {bmatrix} 0\\0\\0\\1\\1 \end{bmatrix} = \begin {bmatrix} 0\\0\\1\\0\\1 \end{bmatrix} (=5) \end{align} \] - \(m_1~から~m_5\) をそれぞれ \(2^1,…,2^5\) で割り、小数点以下を 5 桁まで 2 進数表記します。それをベクトルと看做せば、\(\mathbf v_1^{(i)},~v_2^{(i)},~ v_3^{(i)},~v_4^{(i)},~v_5^{(i)}\) の方向ベクトルとなり、それぞれ列ベクトルとして行列にすれば、生成行列 \(\mathbf V^{(i)}\) が完成です。上の例では、以下の通りです。 \[ \bf {V^{(i)}} = \begin {bmatrix} 1 & 1 & 0 & 1 & 0 \\ 0 & 1 & 1 & 1 & 0 \\ 0 & 0 & 1 & 1 & 1 \\ 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 1 \end{bmatrix}^{(i)} ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ \] 例として、k=1 から 8 までのソボル列を作ってみます。d=2 として、ひとつめの要素は ファンデルコルプト数列を使い、2つ目の要素を、この生成行列を使って生成します。 まず、ひとつめの座標は、ファンデルコルプト数列を使って、1/2,1/4,3/4,1/8,5/8,3/8,7/8,1/16 となります。 ふたつ目の座標は、 \[ \begin {bmatrix} 1 & 1 & 0 & 1 & 0 \\ 0 & 1 & 1 & 1 & 0 \\ 0 & 0 & 1 & 1 & 1 \\ 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 1 \end{bmatrix}^{(i)} \begin {bmatrix} 1\\0\\0\\0\\0 \end{bmatrix}~~mod~~2 =\begin {bmatrix} 1\\0\\0\\0\\0 \end{bmatrix} = \frac 1 2 ~~~~~~~~ \] \[ \begin {bmatrix} 1 & 1 & 0 & 1 & 0 \\ 0 & 1 & 1 & 1 & 0 \\ 0 & 0 & 1 & 1 & 1 \\ 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 1 \end{bmatrix}^{(i)} \begin {bmatrix} 0\\1\\0\\0\\0 \end{bmatrix}~~mod~~2 =\begin {bmatrix} 1\\1\\0\\0\\0 \end{bmatrix} = \frac 3 4 ~~~~~~~~ \] \[ \begin {bmatrix} 1 & 1 & 0 & 1 & 0 \\ 0 & 1 & 1 & 1 & 0 \\ 0 & 0 & 1 & 1 & 1 \\ 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 1 \end{bmatrix}^{(i)} \begin {bmatrix} 1\\1\\0\\0\\0 \end{bmatrix}~~mod~~2 =\begin {bmatrix} 0\\1\\0\\0\\0 \end{bmatrix} = \frac 1 4 ~~~~~~~~ \] \[ \begin {bmatrix} 1 & 1 & 0 & 1 & 0 \\ 0 & 1 & 1 & 1 & 0 \\ 0 & 0 & 1 & 1 & 1 \\ 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 1 \end{bmatrix}^{(i)} \begin {bmatrix} 0\\0\\1\\0\\0 \end{bmatrix}~~mod~~2 =\begin {bmatrix} 0\\1\\1\\0\\0 \end{bmatrix} = \frac 3 8 ~~~~~~~~ \] \[ \begin {bmatrix} 1 & 1 & 0 & 1 & 0 \\ 0 & 1 & 1 & 1 & 0 \\ 0 & 0 & 1 & 1 & 1 \\ 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 1 \end{bmatrix}^{(i)} \begin {bmatrix} 1\\0\\1\\0\\0 \end{bmatrix}~~mod~~2 =\begin {bmatrix} 1\\1\\1\\0\\0 \end{bmatrix} = \frac 7 8 ~~~~~~~~ \] \[ \begin {bmatrix} 1 & 1 & 0 & 1 & 0 \\ 0 & 1 & 1 & 1 & 0 \\ 0 & 0 & 1 & 1 & 1 \\ 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 1 \end{bmatrix}^{(i)} \begin {bmatrix} 0\\1\\1\\0\\0 \end{bmatrix}~~mod~~2 =\begin {bmatrix} 1\\0\\1\\0\\0 \end{bmatrix} = \frac 5 8 ~~~~~~~~ \] \[ \begin {bmatrix} 1 & 1 & 0 & 1 & 0 \\ 0 & 1 & 1 & 1 & 0 \\ 0 & 0 & 1 & 1 & 1 \\ 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 1 \end{bmatrix}^{(i)} \begin {bmatrix} 1\\1\\1\\0\\0 \end{bmatrix}~~mod~~2 =\begin {bmatrix} 0\\0\\1\\0\\0 \end{bmatrix} = \frac 1 8 ~~~~~~~~ \] \[ \begin {bmatrix} 1 & 1 & 0 & 1 & 0 \\ 0 & 1 & 1 & 1 & 0 \\ 0 & 0 & 1 & 1 & 1 \\ 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 1 \end{bmatrix}^{(i)} \begin {bmatrix} 0\\0\\0\\1\\0 \end{bmatrix}~~mod~~2 =\begin {bmatrix} 1\\1\\1\\1\\0 \end{bmatrix} = \frac {1} {16} ~~~~~~~~ \] 以上を組み合わせて、d=2 のソボル列は \[ \left(\frac 1 2,~\frac 1 2 \right)~~~\left(\frac 1 4,~\frac 3 4\right)~~~ \left(\frac 3 4,~\frac 1 4 \right)~~~\left(\frac 1 8,~\frac 3 8 \right)~~~ \left(\frac 5 8,~\frac 7 8 \right)~~~\left(\frac 3 8,~\frac 5 8 \right)~~~ \left(\frac 7 8,~\frac 1 8 \right)~~~\left(\frac {1}{16},~\frac {15}{16} \right) \] となります。ちなみに、k=0 に対応する点は原点 (0,0) になりますが、これをシミュレーションに加えるかどうかは、QMCS 上必要かどうかで判断すればいいでしょう。
< 方向ベクトル \(\bf v_j^{(i)}\)の初期値の決め方 >
先ほどの例で、方向ベクトル \(\bf v_j^{(i)}\) の初期値 \(\bf v_1^{(i)},...,v_s^{(i)}\) を決める為に、まず2進数 \(m_1,…,m_s\) を用意しました。これらの数は、\(m_1 \lt 2^1,~~m_2 \lt 2^2,…,~m_s \lt 2^s\) となる奇数であればよく、任意に選択できます。しかし、d次元の点ベクトルを生成するには、d個の生成行列を用意する必要があり、それぞれの方向ベクトルの初期値として、同じ \(m_1,…,m_s\) を使うと、最初の \(2^s-1\) までは、同じ数を生成する事になります。すると、超立方体の内部での点列の一様分布性が若干劣る事になります。
そこで、Sobol は、一様分布性を測る基準を設け、それを満たすような初期値のリストを提示しています。その基準とか、基準を満たす生成行列の条件などについての説明は、説明能力が無いので飛ばします。ここでは Sobol が提示した、その一定の基準を満たすような初期値のリストを次元20まで示すだけに留めます。実務家としては、それをありがたく使わせて頂くだけです。(下の表で、カッコで括っている数は、初期値から再帰式を使って導出したものです)
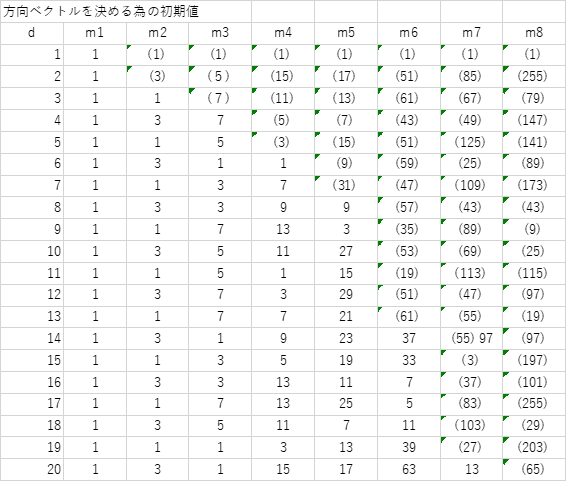
Low Discrepancy Sequence の説明については、これ位にしておきます。私自身あまりよく理解できておらず、詳しい解説は、Paul Glasserman本や、冒頭に紹介した文献等を参考にして下さい。