上級編 6. Libor Market Model
6.6 モンテカルロシミュレーション
6.6.3 乱数の生成方法
6.6.3.3 Low Discrepancy Sequence (超一様分布列、低食い違い数列、準乱数列)
6.6.3.3.2 Discrepancyの定義
\([0,1)^d\) 上に生成された有限個の点列 \({x_1,x_2,…,x_N}\) が、どの程度、一様分布からずれているかを測る尺度として、Discrepancy(食い違い度)と呼ばれる数値があります。まずその定義だけ簡単に説明しておきます。
まず空間 \([0,1)^d\) の部分集合族を \(\mathscr{A}={A_1,A_2,…}\) と表記し、各部分集合 \(A_i\) のルベーグ測度を \(Vol(A_i)\) と表記します。そして \(\mathscr{A}={A_1,A_2,…}\) を次のように定義したとします。
\[ \mathscr{A} ≡ \{ A \vert A∈ \prod_{j=1}^d [u_j,v_j) \},~~~~0 \leq u_j \lt v_j \lt 1, \]すると、部分集合族 \(\mathscr A\) は、Unit Hyper Cube(単位超立方体)\([0,1)^d\) の内部にある、すべての超直方体の集合になります。そして、与えられた点列 \({x_1,x_2,…,x_N }\) の一様分布度合いを、この部分集合族を使って、下記のように定義します。
\[ D(x_1,…,x_N: \mathscr{A}=\sup_{A∈\mathscr {A}} \left| \frac {\sharp \{x_i ∈A \} }{N}-Vol(A) \right| \]但し、\(\sharp \{ x_i∈A\} \) は、点列 x のうち、集合 A に含まれている点の数で、\( \sharp \{x_i ∈A\} / N \) は、A 内のサンプル数で計測された確率に相当します。一方 Vol(A) は、超立方体内での A の確率測度になります。これが、Discrepancy の定義になり、D と表記します。
さらに、その超直方体の集合族を
\[ \mathscr{A} ≡ \{ A \vert A∈ \prod_{j=1}^d [0,u_j) \},~~~~0 \leq u_j \lt 1, \]と定義した場合、すなわち、超直方体のひとつの角が必ず原点にくるようにした場合、その集合族に対する Discrepancy を Star-Discrepancyと呼び D* と表記します。 この D あるいは D* が小さければ、点列xは、より一様分布に近いと見做せます。
この D* は、Low Discrepancy Sequence を使った QMCS の推定誤差に上限を設定する指標となります。ここでは定義だけの紹介にとどめ、数学的な説明は、先ほど紹介した文献を参考にして下さい。
6.6.3.3.3 ファンデルコルプト数列(van del Corput sequence)
ファンデルコルプト数列(van del Corput sequence)は、一次元の\([0,1)\) 間を、均等に分割する点列の生成方法で、他の Low Discrepancy Sequence 生成の基本となるアルゴリズムです。簡単に説明すると、基底となる素数 b を決め、\([0,1)\) 間を b 分割し、分割された各区間をさらに b 分割して、それを繰り返す事により、\([0,1)\) 間を細かく分割していくアルゴリズムになります。その点列を生成する順番は、非負の整数0,1,2,… に対応させており、具体的には以下の通りです。
まず base(基底)となる素数 b を決めます。すると、すべての非負整数 \({0,1,2,…}\) は、基底のべき乗の線形結合で表現できます。すなわち、ある整数を k とすると、
\[ k=\sum_{j=0}^∞ a_j(k)~b^j= a_0(k)~b^0 + a_1(k)~b^1 + a_2(k)~b^2+ ⋯ \]となります。但し、2 のべき乗による級数表現では、係数 \(a_j(k)\) は 0 か 1 しかとらず、かつ有限個の項を除いて \(a_j(k)=0\) となります。各項の係数を冪の大きい順番に並べた場合自然数 kの 2進数表記になります。
例えば、仮に b=2 とし、k=12 とすれば
\[ 12=0×2^0+0×2^1+1×2^2+1×2^3+0×2^4+⋯ \]となり、冪の大きい順に並べた係数ベクトル 1101 は、12 の2進数表現になります。
この係数ベクトルを使って、下記のような変換式を定義します。
\[ \psi_b(k)=\sum_{j=0}^∞ \frac {a_j(k)}{b^{j+1}},~~~ k=0,1,2,… \]すると、\(\psi_b(k)\) は、\([0,1)\) 間の少数に変換されます。これが、ファンデルコルプト 数列になります。b=2 を使って、k が 0 から 16 に対応する \(\psi_b(k)\) は以下のようになります。
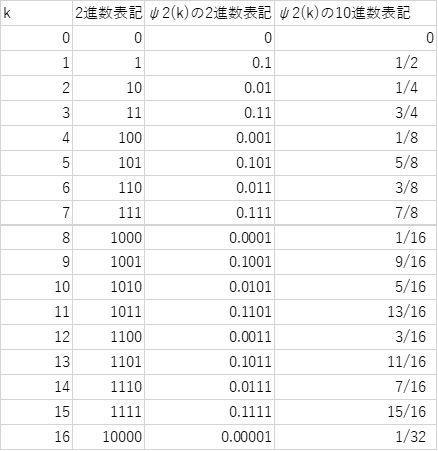
その生成方法は、極めて規則的で予測可能なので、無作為抽出が要求されるゲームアプリなどでは使えませんが、すべての数列を \(b^n\) だけ生成した後の分布は、一様分布との乖離が極めて小さい(low discrepancyな)分布が得られます。 一次元の QMCS ならば、この数列で十分です。