1. QuantLibを使ってみる
1.2 Example を試す
1.2.7 Gaussian1dModels : Gaussian Short Rate Model と Markov Functional Model
1.2.7.3 Gaussian1dModels パート3
ここまでは、期間 10 年の金利スワップを対象資産とするバーミューダ・スワップションの価格を、GSR モデルを使った価格エンジン(Gaussian1DNonstandardSwaptionEngine)で計算するテストでした。
次に、 CMS(Constant Maturity Swap)を対象資産とするバーミューダ・スワップションの価格計算を行っています。ここでは、10 年の Constant Maturity Swap インデックス 対 6ヶ月の Euribor インデックスの、変動金利同士のスワップで、スワップの期間は 10 年とします。また Swaption の行使日は、年 1 回のバーミューダン・タイプとします。この CMS スワップションを、GSR モデルと Markov Functional Model を使って価格計算しています。それぞれにつき、順番に解説します。
1.2.7.3.1 CMS スワップションを GSR で価格評価
まず、価格評価の対象となる商品オブジェクトを作成します。これまでと同じように、まず対象スワップ(ここでは CMS )を作成し、次に、それを対象とするバーミューダ・スワップションを作成します。そして、価格エンジンを生成して、その商品オブジェクトに設定します。価格評価の前に、モデルパラメータの Calibration を行い、最後に NPV()メソッドを呼び出せば価格が計算されます。以下にその手順を順番に見ていきます。
(1) 対象スワップの生成
ここで価格評価しようとしている商品は、CMS(Constant Maturity Swap)を対象としたバーミューダ・スワップションです。CMS の詳しい商品性については、ネットで様々な解説が出ているので、そちらをご覧下さい。もともとイールドカーブの傾斜が急な時代に人気の出た商品ですが、円をはじめ、主要通貨でイールドカーブの勾配が緩く、かつ超低金利環境ではすっかり魅力を失いました。2000 年代後半以降は、ほとんど新規取引を見かけません。ただ、かつて取引された CMS が証券会社や投資家のポジションに残っており、時価評価は必要です。新規取引がほとんど無い中、適正な時価評価が課題になっています。CMSは、オプションが全く付されていないとしても、CMS クーポンの Convexity が強い為、オプション性を持っています。また、CMS 対 LIBOR のスワップでは、価格がイールドカーブの形状に大きく影響されます。その為、適正な価格評価には、本来は金利間の相関まで取り込めるオプションモデルが必要になり、かつ価格評価は非常に困難です。その CMS にバーミューダタイプのオプションが付くと、価格評価はさらに複雑になります。
484 行目に、いまから作ろうとしている CMS バーミューダ・スワップションの概要がコメントされています。対象スワップは、片方のキャッシュフローが 10 年物 CMS レートにリンクしており、反対側のキャッシュフローが6か月 Euribor の変動金利です。スワップの満期は 10 年で、1 年ごとにバーミューダタイプのオプション行使が可能です。
489 行目で、まず CMS 商品オブジェクトを作成しています。CMS は変動金利同士の交換になるので、Swap クラスの派生クラスである FloatFloatSwap クラスを使ってオブジェクトを生成します。基本的な部品は、既に作成済みなので、それを FloatFloatSwap クラスのコンストラクターに渡して出来上がりです。コンストラクターに渡されている引数は、QuantLib の Reference Manual で確認して下さい。一般的な CMS スワップが、どういう部品から作られているか判ると思います。念のため、簡単なコメントを付します。
ext::shared_ptr < FloatFloatSwap> underlying4(new FloatFloatSwap(
VanillaSwap::Payer, :スワップのタイプ。ここではCMSのPayer Swap
1.0, :CMS側のみなし元本
1.0, :Euribor側のみなし元本
fixedSchedule, :CMS側のキャッシュフロー日。187行目で作成済
swapBase, :CMS側の参照インデックス。251行目で作成済
Thirty360(), :CMS側キャッシュフローの日数計算方法
floatingSchedule, :Euribor側のキャッシュフロー日。190行目で作成済
euribor6m, :Euribor側の変動金利インデックス。159行目で作成済
Actual360(), :Euribor側キャッシュフローの日数計算方法。
false, :中途でのみなし元本交換フラッグ False(無し)に設定
false, :最終期日でのみなし元本交換フラッグ False(無し)に設定
1.0, :CMS側のギアリング(通常は倍率1)
0.0, :CMS側のスプレッド 0
Null<Real>(), : CMS側のCapレート 無し
Null<Real>(), : CMS側のFloorレート 無
1.0, :Euribor側のギアリング(通常は倍率1)
0.0010 :Euribor側のスプレッド。ここでは10bpに設定
)); これで対象スワップのインスタンスが出来ました。
(2) バーミューダ・スワップションの生成
次に、これを対象としたバーミューダタイプのスワップションを生成します。494 行目にある通り、FloatFloatSwaption クラスのコンストラクターに、部品となる“対象スワップ:underlying4”と、“オプション行使条件:exercise”を渡して出来上がりです。
(3) 価格エンジンの生成
さらに、497 行目で、この商品用の価格エンジンを生成してます。ここでは GSR モデルを使った Gaussian1dFloatFloatSwaption クラスの価格エンジンを作っています。Discounting Curve としてOIS カーブが渡されている点に注意して下さい。これも、部品は既に作成済みなので、それをコンストラクターに渡して出来上がりです。CMS のスワップションを1ファクターの Hull-White モデルで価格評価をするのは限界があり、実務では使われていません。しかし、後で Markov Functional Model での価格評価と比較するためのテストと思われます。
(4) CouponPricerを使って、対象スワップであるCMS自体の価格を計算
GSR を使った価格エンジンでの価格評価を行う前に、CouponPricer を使った CMS クーポンの価格評価を行っています。
CMS は、表面的にはオプション契約ではありませんが、CMS インデックス金利と、それを割引く為の金利の確率過程が異なってくる為、CMS キャッシュフローには強い Convexity が発生します。すなわち、オプションに近い商品特性を持つという事です。3か月物金利先物で、限月までの期間が長い場合、Convexity Adjustment が必要になりますが、それと似たような理屈です。従って、その価格評価には、何等かの金利オプションモデルが必要になります。
前の“Bonds”の Example コードの所で、変動金利キャッシュフローの現在価値を計算するためには、変動金利の各 Coupon にそれぞれ CouponPricer と呼ばれる 変動金利 Coupon 専用の価格エンジンを設定する事を説明しました。今回評価しようとする Swaption の対象スワップは、両方とも変動金利 CashFlow であり、それぞれに CouponPricer を設定する必要があります。ここでは、CMS インデックスにリンクする変動金利 Coupon には、LinearTsrPricer (Terminal Swap Rateモデルを使ったConvexity Adjustmentを行うエンジン)を使っています。一方、6カ月Euriborにリンクする変動金利Couponは、BlackIborCouponPricer を使っています。いずれも金利オプションモデルを内包した、Coupon専用の価格エンジンです。
513 と 515 行目で、それぞれの Pricer クラスのインスタンスを生成し、517 と 518 行目で、その Pricer を各変動金利キャッシュフローの Leg に設定しています。(LinearTsrPricerのベースになっているTerminal Swap Rate Modelについては、ここでは説明を省略します。本来なら、価格評価にマルチファクターのTerm-Structureモデルが必要な所で、Blackモデルをベースにした簡便な価格モデルです。QuantLibの開発者によれば、Andersen-Piterbargの“Interest Rate Modelling”のVolume-III 16.3に依拠しているとの事なので、そちらを参照下さい。)
CouponPricer の設定が終われば、次に対象スワップそのものの価格エンジンの設定です。520 行目で、DiscountingSwapEngine オブジェクトを生成し、523 行目で、それを対象スワップに設定しました。この価格エンジンは、単に将来のキャッシュフローを Discounting Curve を使って現在価値に割り引くだけです。DiscountingSwapEngine のコンストラクターには、現在価値に割引く為の Discounting Curve として OIS カーブを渡している点に注意して下さい。
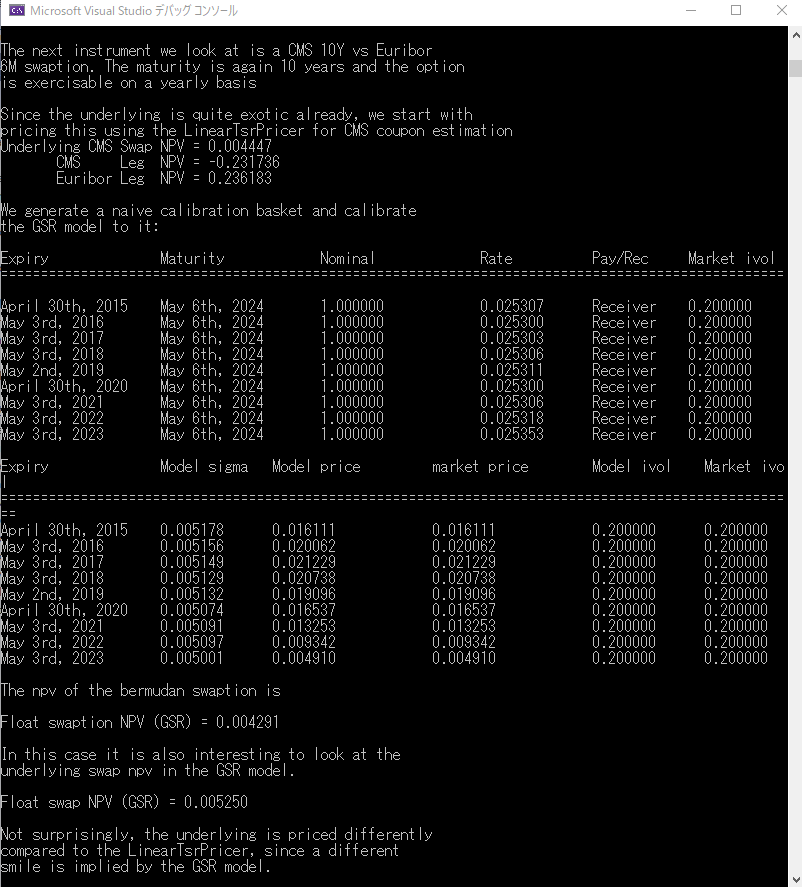
526 行目で商品オブジェクト(underling4)から NPV( )メソッドを呼び出し、価格計算を行っています。計算結果は、下記のコンソール画面の出力にある通り、スワップの NPV は 0.004447(44.47bp)、CMS キャッシュフローの NPV は -0.231736(23.1736%)、Euribor キャッシュフローの NPV は 0.236183(23.6183%)でした。CMSのNPVがマイナス表示なのは、支払いキャッシュフローを意味しています。通常のノーマルなイールドカーブ環境下では、CMS クーポンの現在価値(の絶対値)の方が、ある程度大きな値になるはずですが、ここでは、Euriborキャッシュフローの NPV の方が若干大きくなっています。これは、市場のイールドカーブを2.5%のフラットなイールドカーブと仮定しているからだと思われます。Euribor 側にはスプレッドが 0.1% 乗っかっているので、その分程度が現在価値の差になっています。
(5) CMS Swaptionの価格計算
いよいよGSRモデルを使って、CMS Swaptionの評価を行い所ですが、その前に、まだもう一段階あります。501行目で価格エンジンの設定は終わっていますが、パラメータのCalibrationが未だです。542行目から、まずNaive方式でCalibrationHelperの配列を生成し、そのCalibrationHelperを使って、546行目でCalibrationが実行されました。その結果は、上記のコンソール画面の出力をご覧ください。
最後に、556 行目にある通り、Swaption オブジェクトから NPV( )を呼び出し、価格計算を行っています。結果は、コンソール画面の出力にある通り、0.004291(42.91bp)でした。また、Swaption の対象スワップ自体の NPV は0.00525(52.5bp) でした。
コメントにある通り、GSR モデルでの CMS スワップの NPV と、先ほどの LinearTsrPricer を使った NPV とは、若干異なっています。その理由もコメントに出ています。GSR モデルが内包しているVolatility Smile カーブが、Terminal Swap Rate モデルのそれと異なるからです。
1.2.7.3.2 Markov Functional Model による CMS スワップションの価格計算
さて、ここからは、Markov Functional Model のテストです。573 行目の std::cout のコメントをご覧下さい。
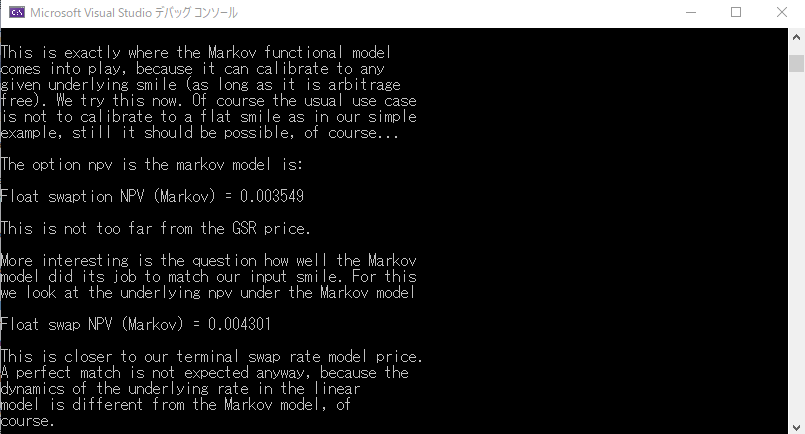
“This is exactly where the Markov functional model comes into play, because it can calibrate to any given underlying smile (as long as it is arbitrage free). We try this now. Of course, the usual use case is not to calibrate to a flat smile as in our simple example, still it should be possible, of course...”
Markov Functional Model は Swaption や CAP の市場価格に内包されている Volatility Smile や Skew に、非常にうまく Calibration できるので、CMS といった商品の価格評価に向いている旨が述べられています。ただし、この Example ではフラットな Volatility Smile カーブのデータを使いますが。
(1) MFMについて
Markov Functional Model(以下‘MFM’)そのものの詳しい説明については、ここでは行いませんが、この Example のテストで必要な範囲内で、必要最小限の説明だけ行います。詳細は、この Example コードを開発した P. Caspers 氏の文献 "Markov Functional Model Implementation in QuantLib","Markov Functional Model(power point presentation)"あるいは、上級編 “Markov Functional Model(マルコフ汎関数モデル)”をご覧下さい。
MFM は、それ以外の金利オプションモデルとは、考え方が根本的に違います。そもそも厳密な意味での“モデル”と呼んでいいのか私には疑問です。Black-Scholes モデルを始めとするオプションモデルはすべて、何等かの経済価値(株価や金利など)が変化していく様子を、
- 簡単なモデル(確率微分方程式)で表現し
- そのモデルから、解析のテクニックを駆使して、将来の株価や金利の確率分布を導出し、
- さらにそれを使ってゼロクーポン債価格や、オプション満期Payoffの期待値(すなわち価格)を導出します。
ところが MFM では、そういった価格や金利そのものの確率変動をモデル化するのではなく、
- まずニュメレール(基準財)となるゼロクーポン債価格の確率分布を求め、
- そのニュメレールとの相対価格の期待値として、ゼロクーポン債価格や金利オプションの価格を導出します。
- しかも、ニュメレール価格の確率分布は、モデル(確率微分方程式)を解析して求めるのではなく、ヨーロピアンオプションの市場価格に内包されているフォワード金利の確率分布から導出されます。
これは、LIBOR-Swap カーブからゼロクーポン債カーブを構築する際の Bootstrapping-Interpolation 法のアルゴリズムと、考え方はよく似ています。Bootstrapping-Interpolation 法により構築されたゼロクーポンカーブは、モデルとは呼ばれていませんよね。それは、LIBOR-Swap カーブをゼロクーポン債カーブに換算しただけで、市場データそのものだからです。なので、MFM を“モデル”と呼んでいいのか疑問だと述べた次第です。
イールドカーブの場合は、一本の Par Curve から一本のゼロクーポン債カーブ(曲線)を導出しますが、それでも相当複雑な計算アルゴリズムになります。MFM の場合は、オプション行使の時間軸と、オプションストライク軸上に、ゼロクーポン債価格の曲面を描くので、アルゴリズムは格段に複雑になります。そのアルゴリズムの詳細は、上級編“Markov Functional Model(マルコフ汎関数モデル)”をご覧下さい。
(2) モデルオブジェクトの生成
Exampleコードに戻ります。
まず価格エンジンの部品となるモデルオブジェクトを生成します。これも部品から組み立てていきます。
581~585 行目で、その部品を作っています。まず 581 行目は、ニュメレール価格が拡散していく様子を離散時間で表現する為に、その時間軸を設定しています。Date オブジェクトの配列ですが、コンストラクターに渡している引数を見ればわかる通り、バーミューダ・スワップションの行使日と同じ時間軸に設定しています。但し、後でモデルを構築する際に、この時間軸は、最長期のキャッシュフロー日付までカバーするように延長されます。
583 行目は、CMS キャッシュフローの Fixing 日の配列を作っています。見ての通り、たった今作った MFM 用の時間軸(但し延長前)と同じ日に設定されています。
584 行目は、MFM の拡散係数を Piecewise Constant な関数として定義し、初期値としてすべて 0.01 に設定しています。MFM の拡散係数とは、ガウス分布すると仮定した状態変数 x(t) の確率微分方程式(下記)の σ(t) の部分です。
\[ dx(t)=σ(t) e^{a(t)t} dW(t) \]585 行目は、CMS キャッシュフローのスワップインデックスがすべて 10 年物のスワップ金利を使うことを示しています。
そして、部品が揃ったので 586 行目で MFM モデルオブジェクトを生成しています。 586 行目にある MarkovFunctional のコンストラクターに渡している部品(引数のリスト)をもう少し詳しくみていきます。(オブジェクトを作成する際、その部品として何が必要かは、Reference Manual で、そのクラスのコンストラクターを確認するのが大事です。)
shared_ptr<MarkovFunctional> markov =ext::make_shared <MarkovFunctional> (
yts6m, : イールドカーブ(インデックスカーブ)
reversion, : 中心回帰強度
markovStepDates, :離散化した時間軸の配列
markovSigmas, :Piecewise ConstantなVolatility関数
swaptionVol, :ベンチマーク商品のBlack Vol Cube
cmsFixingDates, :Swaptionの行使日の配列
tenors, :Swaptionの対象スワップの期間の配列
swapBase, :対象スワップのインデックス
MarkovFunctional::ModelSettings().withYGridPoints(16) :モデルの設定
); ① イールドカーブは、154 行目で作成済みの 6か月 EURIBOR のインテックスカーブです。MFM が生成する将来のゼロクーポン債価格が、この当初イールドカーブにフィットするようにモデルが構築されます。
② 中心回帰強度は、217 行目で設定した値(定数)に設定されます。これは Hull-White モデルの中心回帰強度パラメータと同じ役割を果たしています。この値は、先ほどに示した状態変数 x(t) の確率過程の拡散係数 \(σ(t)e^{a(t)t}~の中にある a(t)\) に該当します。なぜそうなるかは、先ほど紹介した P. Caspers 氏の文献をご覧下さい。
③ 離散化した時間軸の配列は、とりあえずバーミューダ・スワップションの行使日の配列で設定します。但し、MFM 構築の際、オプション行使日、オプション対象スワップ、CMS のインデックスとなるベンチマークスワップの内、最長の時点まで延長し、その各キャッシュフロー日が追加されます。
markovSigmas は 584 行目で作成した MFM の Volatility パラメータの配列です。先ほど示した状態変数の拡散過程の式における σ(t) に該当します。これを Piecewise Constant な関数と仮定し、その初期値の配列(ここではすべて0.01)が渡されます。この値は後で、市場の Swaption Volatility Cube データに Calibration されます。
⑤ swaptionVol は 171 行目で作成済のベンチマーク商品の(Implied Black)Volatility Cube です。ここで使われているデータは、テスト用に便宜的に作っているだけで、3次元の方向すべてについて、同じ値 20% に設定しています。従って、Volatility Smile の形状が Arbitrage Free になっていないかどうかの面倒なチェックは、必要ありません。しかし、実際の市場データを使う場合は、この Volatility Cube のデータの整合性について、細心のチェックが必要です。このデータが非整合的であれば、モデル構築の過程でのアルゴリズムが収束せずエラーを起こします。
⑥ 6 番目と 7 番目の引数、cmsFixingDates、tenors は、Calibration の対象となる Volatility Cube の、オプション Expiry の軸と、対象スワップの期間の軸を指定します。引数名が cmsFixingDates と誤解を招きそうな名前になっているのは CMS の Fixing 日とバーミューダ・スワップションの行使日が同じだからです。
⑦ 8番目の引数 swapBaseは、251 行目で、そのインスタンスが生成されており、それが引数として渡されています。Swap Annuity を計算するために必要な情報を提供します。
⑧ 最後の引数は、MarkovFunctional::ModelSettings( )となっています。ModelSettings クラスは、MarkovFunctional クラスの内部クラスで、MFM を構築するにあたって使われる様々な数値解析テクニックに必要なパラメータ値を保持しています。それらパラメータはすべてデフォールト値が設定されており、とりあえずそのまま使えばいいでしょう。設定値の内容を詳細に理解したい人は、markovfunctional.hpp のソースコードで確認して下さい。この Example では計算速度を上げる為に、yGridPoints をデフォールト値の 64 から 16 に変更しています。ちなみにyGridPoints とは、ゼロクーポン債の確率分布を導出する為に、状態変数空間上の座標の数を指定するものです。Volatility Cube のデータから、各 Expiry 日毎に、スワップ金利の確率分布をこの数だけ導出し、それをゼロクーポン債価格の分布に換算しています。
これで、MFMモデルオブジェクトが出来上がりました。
(3) 価格エンジンの生成
次に、モデルオブジェクトを部品として、価格エンジンを構築しています。ここでは、2種類の価格エンジンを構築しています。
まず 592 行目で、Gaussian1dSwaptionEngine オブジェクトを作成しています。これは Plain Vanilla なヨーロピアンオプションの価格評価用で、CalibrationHelperで使われます。
次に 595 行目で、Gaussian1dFloatFloatSwaptionEngine オブジェクトを作成しています。これは CMS スワップションの価格評価に使います。
それぞれコンストラクターの引数(必要な部品)が異なります。価格エンジンのアルゴリズムの詳細な説明は省略しますが、一点だけ興味深い点を述べておきます。この価格エンジンクラスは、モデルとして GSR を使ったり、MFM を使ったりしてエンジンを組み立てる事ができます。234 行目では GSR を使った価格エンジンオブジェクトを作成しているし、ここでは MFM を使った価格エンジンを作成しています。そもそも、QuantLib では GSR クラスもMarkovFunctional モデルクラスも、同じ Gaussian1dModel クラスから派生しています。クラス名から伺えるように、1 次元のガウス過程を取る確率変数をモデル化している点で、GSR と MFM は共通点があります。また、状態変数の汎関数としてゼロクーポン債価格を定義している点も共通です。さらにそのゼロクーポン債価格の期待値を求める為の数値積分のアルゴリズムも同じです。従って、このようなクラス構造にしたのでしょう。但し、状態変数からゼロクーポン債価格の汎関数を求めるプロセスは、両者で発想が全く異なる点には注意して下さい。GSR と MFM が同じカテゴリーのモデルと理解しようとすると、混乱すると思います。
(4) 価格の計算
商品オブジェクトと価格エンジンオブジェクトが出来上がったので、価格計算は簡単です。これまでと同様、601 行目で、まず商品オブジェクトに価格エンジンを設定し、604 行目で商品オブジェクトから NPV()メソッドを呼び出すだけです。
MFM を使った価格エンジンでの CMS スワップの NPV 計算結果は、コンソール画面の出力にある通り、0.003549(35.49 bp)でした。
(5) Volatility パラメータの Calibration
MFM におけるもう 1つの Calibration について説明します。629 行目の std::cout のコメントをご覧下さい。MFM の概要説明で、MFM は市場で観測されるスワップ金利の確率分布をニュメレールのゼロクーポン債価格の分布に換算していると述べました。このアルゴリズムを、MFM に関する論文や解説では、Volatility Cube のストライク軸(Volatility Smile)への Calibration と呼んでいます。(注:しかし、このアルゴリズムは Calibration というより、Bootstrapping-Interpolation に近いと思います。いずれにしても、これがひとつ目の Calibration です。)
もう1つの Calibration とは、Volatility パラメータの Calibration です。先ほど、MFM の中の確率変数 x(t) の確率過程は、\(dx(t)=σ(t)e^{a(t)t} dW(t)\) と仮定されていると述べましたが、この右辺のパラメータ \(σ(t)\) を Volatility Cube の Expiry 軸のデータに Calibration します。これは、先ほどの GSR モデルの Volatility パラメータの Calibration に近い意味になります。但し、GSR と MFM における状態変数 x(t) の役割は、かなり異なりますが。
CalibrationHelper の配列は、276 行目ですでに作成済です。 配列中の各 CalibrationHelper インスタンスに、先ほど生成した2つの価格エンジンの内、Plain な Swaption 用の価格エンジン(Gaussian1dSwaptionEngineクラスのインスタンス)を設定します。そして、667 行目で Calibration を実行しています。コメントにもある通り、この2番目の Calibration には、相当時間がかかります。理由は、この Calibrationの実行中に、1番目のCalibrationを何度もやりなおしているからです。2番目のCalibrationは、Piecewise ConstantなVolatilityパラメータσ(t)を最小2乗法で最適値を求めていますが、σ(t)の値が動くと、各Expiry日におけるx(t)の分布も動くので、1つ目のCalibrationもやり直す必要があるからです。
Calibration の結果は、下記のコンソール画面の出力をご覧下さい。ここでも、MFM による価格と市場価格が完全にマッチしています。Calibration の対象となる CalibrationHelper(すなわち市場価格)と、モデルのパラメータの数(σ(t)の離散時間の数)が一致している為です。
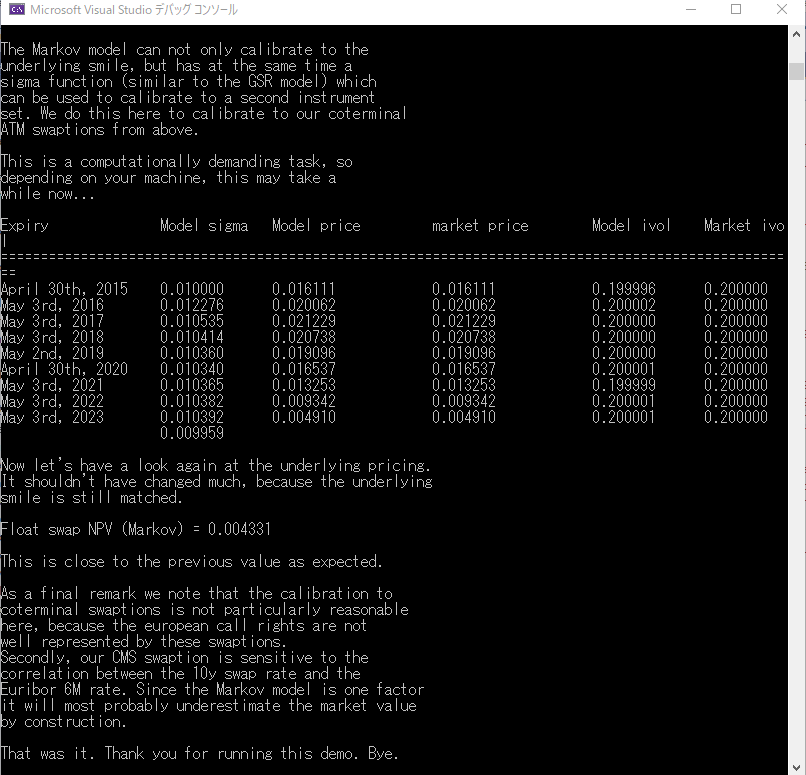
Calibration でパラメータが変更になったので、再度 CMS スワップションの対象スワップの価格を計算しています。計算結果は、0.004331(43.31bp)で、Calibration 前の結果(0.004301)と大きく変わっていません。コメントにもある通り、Volatility データをすべて 20% のフラットと仮定している為です。
687 行目の std::cout のコメントをご覧下さい。2点の注意点を述べています。一点目は、Volatility パラメータのCalibration は、CalibrationHelper が Co-terminal Swaption になっているのは、評価対象のデリバティブズ(Underlying が 10 年物スワップインデックスを対象とする CMS)とマッチしていないので、あまり意味を持たないと述べています。CalibrationHelper を選択する際は、評価しようとするデリバティブズの行使期限や対象スワップの商品性にマッチするようなものを選ぶべきということでしょう。
二点目は、このExampleでテストされたMFMは1ファクターであり、評価対象となるCMSにおいて、スワップインデックスの確率変動と、6カ月EURIBORの確率変動の相関が1と想定している事になるという事です。2ファクターのMFMならこの2つの金利が相関をもって動く様子を表現できますが、QuantLibの中では実装されていません。
このExampleの説明は以上です。
<ライセンス表示>
QuantLibのソースコードを使う場合は、ライセンス表示とDisclaimerの表示が義務付けられているので、添付します。 ライセンス