上級編 6. Libor Market Model
6.6 モンテカルロシミュレーション
6.6.6 アメリカンタイプのオプションへの対応(続き)
6.6.6.2 Random Tree Method
6.6.6.2.1 Random Tree Method の概要
Random Tree Method は、MCS による最も初歩的なバーミューダンタイプのオプション価格計算方法です。原理は単純で、簡単に理解できますが、ダイナミックプログラミングの方法を使って力づくの計算をするので、計算時間が相当かかり、この方法が使える商品は限定的です。原理を簡単に説明すると、
- まず現時点をスタートに、m 個のサンプル経路を、最初のオプション行使日まで生成します。
- そこでオプションを行使するか、行使せずに継続保有するかの判断をしなければなりません(6.126式)。その際、行使価値は簡単に計算できるものの、継続保有価値は直ちに求まりません。そこで、そこをスタートとして、次のオプション行使日までさらに m 個の新たなサンプル経路を生成します。各ノードから m 個のサンプル経路を生成するので、この時点でのトータルのサンプル数は \(m^2\) 個になります。
- 次の行使日が、最終行使日でなければ、やはり継続保有価値は求まらないので、サンプル経路をさらに次の行使日までシミュレーションします。それを最終行使日まで続けます。オプションの行使機会が M 回あるとすると、トータルのサンプル数は \(m^M\) 個になります。
- 最終行使日では、継続保有価値は 0 なので、行使価値=オプション価値 になります。
- その最終行使日のオプション価値を使って、一つ前の行使日の継続保有価値を求めます。継続保有価値は、一つ前の行使日の各ノードからみた、最終行使日におけるオプション価値の条件付き期待値になります。それをシミュレーションされた経路のサンプル平均で近似します。
- その継続保有価値と行使価値を比較し、大きい方をその行使日におけるオプション価値とします。
- その計算を、時間軸を遡及しながら現時点まで遡れば、求めたいオプション価格になります。
この方法では、ファクター数や、期限前行使日の数が多くなると、サンプル数が幾何級数的に大きくなるので、原則として、ファクター数が限られた(1~2)モデルで、限られたオプション行使機会を持つバーミューダンタイプのオプションにしか対応できません。
注:ただ、行使回数が多いバーミューダンタイプのオプションであっても、主要な行使日を5~6回特定してそれ以外の行使日を無視したとしても、オプション価値はそれほど大きくは変わりません。従って、それを近似値としてオプション価格と見做す考え方もあります。アメリカンオプションであっても、適当な時点を数回選び、この方法で価格を計算すれば、理論値からそれほど大きく離れていない近似値は求まります。多くの行使機会を無視して計算するので、価格の下方バイアスがかかりますが、他の MCS の方法や、有限差分法、2 項モデル・3 項モデルであっても、アメリカンオプションの価格評価は、僅かに下方バイアスがかかった近似値でしかありません。要は、それによる誤差が許容範囲内に収まるかどうかです。
6.6.6.2.2. アルゴリズム
アルゴリズムをもう少し詳しく説明します。
- 現時点を t=0、確率変数値を \(x(0)\) とし、そこから最初の期限前行使日である \(T_1\) 時点まで、m 個のサンプル経路を生成します。そのサンプル値を、\(x_1^{(j)},~~j=1,2,…,m\) と表記します。下付け文字の数字が、行使日 \(T_1\) に対応するインデックスで、上付け文字 \((j)\) は、その時点におけるサンプルのノードを示すインデックスです。
- すると、\(T_1\) 時における各ノード上のオプション価値は、行使価値と継続保有価値の高い方になるので、6.126 式から、下記式で決まります。
\[
V_1(x_1^{(j)})=\max\left[h_1\left(x_1^{(j)}\right),~E\left[V_2(x_2)~|~x_1^{(j)}\right] \right],~~~~j=1,…,m
\]
但し、\(h_i(x_i)~ と~V_i(x_i)\) はいずれも、ニュメレールで基準化された値とします。従って、max 関数内の期待値演算は、そのニュメレールに対応する確率測度下での期待値演算になります。
- 右辺の \(E\left(V_2(x_2)~|~x_1^{(j)}\right)\)(=継続保有価値/Numeraire)は、\(T_1\)以降のxの確率分布を使って求める必要があります。その確率分布をシミュレーションする為、\(x_1^{(j)}\) をスタートとし、次のオプション行使日の \(T_2\) まで、新たなサンプル経路を m 個生成します。そうやって生成された \(T_2\) 時におけるサンプル値を \(x_2^{(jk)}, ~~ k=1,2,…,m\) と表記します。\(T_1~時に~m\) 個のサンプル経路があり、そこからそれぞれ m 個のサンプル経路を生成するので、\(T_2\) 時のサンプル経路数は \( m^2 \)になります。
- \(T_2\) 時の各ノードにおける継続保有価値\(=E\left(V_3(x_3)~|~x_2^{(jk)}\right)\) は、やはり不明なので、\(T_2\) 時の各ノードからさらに次の行使日まで新たなサンプル経路を生成します。そうやって生成された \(T_3\) 時におけるサンプル値を \(x_3^{(jkl)},~~l=1,2,…,m\) と表記します。
- そのステップを、最終行使日まで繰り返します。そうやって生成された最終期日におけるサンプル値を \(x_M^{(jkl…z)},~~z=1,2,…,m\) と表記します。上付け文字にある\((jkl…z)\) が、サンプル経路を示すインデックスになります。
すなわち、サンプル経路が、各行使日を起点に次々と枝分かれしていきます。図で示すと下記のようなイメージです。
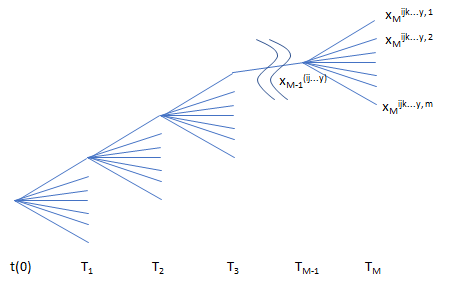
図で分る通り、オプション行使日の数が増えると、サンプル数が幾何級数的に増加します。各行使時点のサンプル数が m、オプション行使日の数が M とすると、必要な総サンプル数のオーダーは \(O(m^M)\) となります。(その数を減らす為のテクニックがいくつかあり、後で紹介します)
- サンプル経路が、最終行使日に到達すれば、各ノード上のオプション価値は、オプションの行使価値に一致します。すなわち、
\[
\hat{V}_M \left(x_M^{(j…,z)}\right) =h_M \left(x_M^{(j…,z)}\right),~~~~z=1,2,…,m
\]
但し、Vにハットの付いた \(\hat{V}_i\left(x_i^{(jk…)}\right)\) はサンプル値を示すものとし、ハットの無い \(V_i\left(x_i^{(jk…)}\right)\) は理論値を示すものとします。
- 今度は、この \(T_M\) 時のオプション価値を使って、\(T_{M-1}\) 時のオプション価値を求めます。\(T_{M-1}\) 時の確率変数の値が \(x_{M-1}^{(jk…y)}\) だとすると、そこでのオプション価値は、下記式で求まります。
\[
V_{M-1}\left(x_{M-1}^{(j…y)}\right)
=\max\left[h_{M-1}\left(x_{M-1}^{(j…y)}\right),E\left[V_M\left(x_M^{(j…y,z)}\right)~|~ x_{M-1}^{(j…y)}\right]\right],
~~~~y=1,…,m
\]
この式の右辺にある条件付き期待値の式を、 \(T_M\) 時のオプション価値のサンプル平均を使って近似します。すなわち
\[
E\left[V_M \left(x_M^{(j…yz)}\right)~|~x_{M-1}^{(j…y)} \right]
≈ \frac 1 m \sum_{z=1}^m \hat{V}_M \left(x_M^{(j…y,z)}\right)
\]
これを使って、上式に代入すると
\[
\hat{V}_{M-1} \left(x_{M-1}^{(j…y)}\right)
= \max\left[h_{M-1}\left(x_{M-1}^{(j…y)}\right), \frac 1 m \sum_{z=1}^m \hat{V}_M \left(x_M^{(j…y,z)}\right)\right]
\]
となります。これで、\(T_{M-1}\) 時のオプション価値が求まりました。
- さらに 7.で求まったオプション価値から、時間軸を遡及しながら各行使日におけるオプション価値を求めていきます。\(T_1\) 時まで遡及した時のオプション価値は、 \[ \hat{V}_1 \left(x_1^{(j)}\right) =\max\left[h_1 \left(x_1^{(j)} \right), \frac 1 m \sum_{k=1}^m \hat{V}_2 \left(x_2^{(jk)}\right) \right] \] となります。さらに最終的に現時点\((t=0)\)のオプション価値は、 \[ V_0 (x(0)) ≈ \hat{V}_0 (x_0) = \frac 1 m \sum_{j=1}^m \hat{V}_1 \left( x_1^{(j)} \right) \] で求まります。こうして求まった MCS によるサンプル平均は、モデルが想定する理論値に対する近似値になります。
6.6.6.2.3 バイアス
さて、上のアルゴリズムで求まった近似値は精確ではなく、以下のような推定誤差とバイアスが含まれています。
- 連続時間のモデルを離散時間で近似した事による推定誤差
- サンプル値の分散から生じる推定誤差
- オプション行使日を制限した事による価格下方バイアス(アメリカンオプションの場合)
- 条件付き期待値の計算を、将来のサンプル値で近似した事による価格上方バイアス
これらの内、1.の離散化誤差については、前のセクションで、原因と対処法について既に説明しました。また、2.の推定誤差については、分散低減法のセクションで、いくつかの対処法を説明しました。3.のバイアスについては、より多くのオプション行使日でのオプション価値を計算すれば、低減できますが、Random Tree Methodsでは、限界があります。バイアスを甘んじて受け入れるか、オプション行使回数が多い商品では、この方法を使うのをあきらめるしかありません。
さて、1.~3.の誤差要因が何等かの方法で許容範囲内に収まったとして、残った 4.のバイアスをどうするかです。その前に、この価格バイアスはどういう要因で発生するのかみてみます。
まず、バーミューダンタイプのオプションの期限前行使日における理論値は、6.126 式の通りです。
\[ V_i(x_i)=\max \left(h_i(x_i),c_i(x_i)\right) = \max\left(h_i(x_i),E\left[V_{i+1}(x_{i+1})~|~x_i \right]\right) \tag{6.126} \]すなわち、期限前行使日において、確率変数の値が \(x_i\) だった場合、そこで行使価値と、行使せずに次回の行使日以降のオプション価値の期待値を比較し、より価値の高い方を選択して得られる価値となります。しかし、\(E(V_{i+1}(x_{i+1})~|~x_i)\) は、モデルが想定する将来の x の分布から導出される理論値になりますが、それが解析的に求まらないから MCS を行う訳です。一方、Random Tree Methods では、右辺の max 関数の中にある期待値計算を、シミュレーションされた次回行使日以降のサンプルを使って導出するものです。シミュレーションなので、実行する度に異なった値になりますが、その期待値は下記式のようになります。
\[ E\left[ \hat{V}_i(x_i^{(j…,y)})\right] =E\left[\max\left[h_i \left(x_i^{(j…,y)}\right), \frac 1 m \sum_{z=1}^m \hat{V}_{i+1}\left(x_{i+1}^{(j…y,z)}\right) \right] \right] \]すると、次のような不等式が成立し、シミュレーションによるオプション価格は、理論値に対し上方バイアスがかかります。
\[ \begin{align} E\left[\hat{V}_i \left(x_i^{(j…,y)}\right)\right] & =E\left[\max\left(h_i\left(x_i^{(j…,y)}\right), \frac 1 m \sum_{z=1}^m \hat{V}_{i+1}\left(x_{i+1}^{(j…y,z)}\right)\right)\right] \\ & ≥ \max \left(h_i \left(x_i^{(j…,y)}\right), E\left[\frac 1 m \sum_{z=1}^m \hat{V}_{i+1}\left(x_{i+1}^{(j…y,z)}\right)~|~x_i^{(j…,y)} \right] \right) \tag{6.127} \end{align} \]上方バイアスがかかる理由は、数学的には、ジェンセンの不等式によるものです。上式にある max 関数は凸関数であり、期待値を計算してから max 関数を評価するのと、max 関数を評価してから期待値を計算するのでは結果が異なります。ジェンセンの不等式では、後者の方が大きくなります。すなわち上記の2行目の不等式が成立します。さらに、Random Tree Methodsでは、最終行使日から遡及する際、1ステップごとに上方バイアスがかかった値が計算されるので、それが積み重なったいきます。
また、上方バイアスがかかる理由を、直観的に説明すると、本来わからないはずの将来の情報を使って、条件付き期待値を計算し、それを継続保有価値と看做しているからです。
この価格上方バイアスは、派生させるノード数 m を大きくすれば、中心極限定理により 0 に収束していきます。しかし、Random Tree Methods では、むやみに m を大きくできないので、一定程度の上方バイアスは甘受せざるを得ません。しかしそれでは、真のオプション価格が、サンプル平均を中心とする信頼区間の中に存在しているかどうか分かりません。
そこで、真の価格がどの辺りにあるか知る為に、同じ Random Tree Methods を使って、価格の下方バイアスがかかるアルゴリズムを構築します。すると、上方バイアスのかかった信頼区間と、下方バイアスのかかった信頼区間をオーバーラップさせれば、真の理論値が、一定の確率でその区間のどこかにあるであろう事が推察できます。では、以下に下方バイアスがかかるアルゴリズムを説明します。
その基本的な考え方は、max 関数の判断に必要な継続保有価値の計算用サンプルと、判断後に使う実際の継続保有価値の計算用サンプルを、それぞれ分けるというものです。あるノードから派生する m 個のサンプルを、独立した2つのグループに分けます。 すなわち \( \dot{m}_1+\dot{m}_2=m \)。この内、 \(\dot{m}_1\) のサンプルを継続保有価値計算の判断に使い、\(\dot{m}_2\) のサンプルを、実際の継続保有価値として使います。その上で、max 関数の評価を、下記のよう行います。
\[ \begin{eqnarray} \begin{cases} if ~~~~\frac {1}{\dot{m}_1}\sum_{z=1}^{\dot{m}_1} \hat{V}_{i+1}\left(x_{i+1}^{(j…y,z)}\right) \leq h_i\left(x_i^{(j…y)}\right), ~~~~ then ~~~~ h_i\left(x_i^{(j…y)}\right) \\ else ~~~~ \frac {1}{\dot{m}_2} \sum_{z=1}^{\dot{m}_2} \hat{V}_{i+1} \left(x_{i+1}^{(j…y,z)}\right) \end{cases} \end{eqnarray} \tag{6.128} \]このようにすれば、先ほどのアルゴリズムに内包していた上方バイアスが取り除かれ、逆に下方バイアスがかかります。というのは、\(\dot{m}_1\) 個のサンプルで導出された継続保有価値は、真の期待値と必ずしも一致しないので、そのずれた値を使った判断は、最適行使戦略と言えないからです。\(\dot{m}_1~~と~~\dot{m}_2\) のサンプル数をそれぞれどうするかは、様々な選択肢があります。Broadie-Glasserman の論文(“Pricing American-style securities by simulation”)では、\(\dot{m}_1~~を~~m-1~とし,~\dot{m}_2\) を残りの 1 個のサンプルとする方法が紹介されています。但し、\(\dot{m}_1\) の選択を、\(\dot{m}_2\) が異なるような選択を何回も行い、そうやって選択された \(\dot{m}_2\) の平均を、継続保有価値として使うものです。
このように、オプションを期限前行使するかどうかの判断に使う継続保有価値の計算と、実際に使う継続保有価値を分けるというテクニックは、MCS でアメリカンタイプのオプション価格を計算する際に、よく使われるものです。
6.6.6.2.4 計算負荷の軽減方法
上記のアルゴリズムを、実際にコンピュータープログラムに落とし込むと、サンプル数は \(\dot{m}_1^M +\dot{m}_2^M\) 必要となり、通常のモンテカルロシミュレーションに比べ格段に計算負荷が大きくなります。そこで、計算負荷を少しでも軽減させるようなアルゴリズムがいくつか提案されています。以下にGlasserman本で紹介されている2つの方法を紹介します。
< 計算負荷の軽減方法 ① : Depth-First Processing >
Random Tree Methodsの一番の問題は、サンプル数が幾何級数的大きくなる事です。すると、サンプル生成そのものに、相当時間がかかる上、もし生成されたサンプルをすべて同時にヒープメモリーに保持してしまうと、CPU によるメモリー管理に非常に負荷がかかり、計算が一段と遅くなってしまいます。そこで、Glasserman 本では Depth-First Processing という方法が紹介されています。具体的には、以下のようなコンピューターアルゴリズムにより、すべてのサンプルを同時に生成するのではなく、各ノードにおいて継続保有価値を計算するのに必要最低限のサンプルだけを生成し、計算が終わればそのサンプルをメモリーから消去してしまうものです。
- まずサンプル経路を一本、最終行使日のひとつ手前の行使日まで生成する。そこから、最終行使日まで、m回のシミュレーション経路を生成します。そうやって生成された最終期日のサンプル値は、\(x_M^{(j…y,z)},~~z=1,…,m\) と表記されますが、上付け文字の (j…y,z) が、サンプル経路を示すインデックスになります。\(x_M^{(j…y,z)},~z=1,…,m\) の表記が示すのは、(j…y) までは同じ経路で、そこから最後の経路が m 個生成される事を示します。
- その内最初に生成されたサンプル経路を \((1,…,1,z),~~z=1,…,m\) とします。この m 個のサンプル経路ごとに、最終行使日の Payoff 関数をあてはめれば、
\[
h_M \left(x_M^{(1…1,,z)}\right) = \hat{V}_M \left(x_M^{(1…1,,z)}\right),~~~z=1,…,m
\]
となり、m 個のオプション価値のデータが求まります。
- そのサンプル平均を取れば、\(\hat{V}_{M-1}\left(x_{M-1}^{(1…1)}\right)\) が計算できます。この値を一旦メモリーに保持しておきますが、\(x_M^{(1…1,,z)}~と~\hat{V}_M \left(x_M^{(1…1,,z)}\right),~~z=1,…,m\) のデータはもう不要になったのでヒープメモリーから消去します。
- 次に、\(T_{M-1}\) まで次の一本のサンプル経路を生成し、そこから \(T_M\) 時まで m 個のサンプル経路を生成します。このサンプル経路のインデックスは、\((1,…,2,z),~~z=1,…,m\) となります。ここで、先ほどと同様に最終行使日の Payoff 関数をあてはめれば、\(h_M \left(x_M^{(1…2,,z)}\right) = \hat{V}_M \left(x_M^{(1…2,,z)}\right),~~z=1,…,m\) というオプション価値のデータが求まります。
- さらに先ほどと同様、ここから、\(\hat{V}_{M-1} \left(x_{M-1}^{(1…2)}\right)\) が計算できます。それをメモリーに保持した後、先ほどと同様、\( x_M^{(1…2,,z)}~と~\hat{V}_M \left(x_M^{(1…2,,z)}\right),~~z=1,…,m \) のデータはもう不要になったのでヒープメモリーから消します。
- 以上の操作を、\(T_{M-1}\) 時までの経路、\((1,…,3),(1,…,4),…,(1,…,m)\) すべてで行います。すると、\(T_{M-2}\) 時のサンプル経路 \((1,…,1)\) から派生した経路上のオプション価値 \(\hat{V}_{M-1}\left(x_{M-1}^{(1…1,y)}\right),~~y=1,…,m\) がすべて求まり、そのサンプル平均を取れば、オプション価値 \(\hat{V}_{M-2}\left(x_{M-2}^{(1…1)}\right)\) が求まります。それをメモリーに保管し、不要になったサンプル経路の情報はメモリーから消します。
- 同様に \((1,…,2,1),(1,…,2,2),…,(1,…2,m)~~~、~(1,…3,1),(1,…3,2),…,(1,…3,m)\) と行っていきます。
- 最終的に \((mm…m1),(mm…m2),…,(mm….mm)\) の経路まで行えば、すべてのサンプル経路で必要な計算を行った事になり、\(\hat{V}_1 \left(x_1^{(i)}\right),~~i=1,…,m\) が求まります。そのサンプル平均 \(\hat{V}_0 (x_0)\) が現時点のオプション価格になります。
具体的にどのようにプログラムに落とし込むかは、実践編“QuantLibを使ってみる”の所で、説明する予定です。
< 計算負荷の軽減方法 ② : Pruning >
別の計算負荷軽減方法として、Glasserman 本では Pruning (派生するサンプルの剪定)という方法が紹介されています。もともと Broadie- Glasserman の論文(“Enhanced Monte-Carlo estimates of American option pricing ”)で紹介されたものです。
仕組みは、簡単で、オプションを期限前行使するかどうかの判断、すなわち
\[ V_i(x_i)=\max \left[ h_i(x_i), E\left( V_{i+1}(x_{i+1})~|~x_i \right) \right] \]の計算において、もし行使価値 \(h_i(x_i)\) が継続保有価値を明らかに下回るのであれば、継続保有価値のシミュレーションをせず、次の行使期日までサンプル経路をそのまま伸ばすだけにするものです。行使価値が継続保有価値を明らかに下回るかの判断は、例えば
- オプションが、その経路上で Out of the Money であれば、行使価値 = 0 なので、明らかに継続保有する。
- もし、経路上で、同じ Payoff のヨーロピアンオプション価格が簡単に求まるのであれば、行使価値とそれを比較し、行使価値が上回っている場合のみ、継続保有価値のシミュレーションを行う。なぜなら、アメリカンタイプのオプション価値はヨーロピアンオプションの価値を必ず上回るので、行使価値がヨーロピアンオプション価格さえ下回るのなら、期限前行使しないのは明らかだからです。(この方法の削減効果は絶大です)
- 最終行使日のひとつ手前の行使日 \(T_{M-1}\) においては、オプション行使があと1回しか残っていないので、継続保有価値として、シミュレーションで計算せずに、同じ満期で同じ Payoff をもつヨーロピアンオプション価格を使う。
これらの方法により、継続保有価値を計算する為の派生シミュレーションの数を大幅に減らす事ができます。アメリカンタイプのオプションでも、期限前行使する可能性がある領域は、Deep In the Money の領域で、それほど広くありません。という事は、大半のサンプル経路で、継続保有価値を別途シミュレーションする必要はないのです。
この他にも、色々工夫すれば、計算時間を短縮する方法がいくつか見つかるかも知れません。具体的なアルゴリズムは、商品毎に考える必要があり、実務では、各会社の Quants Analyst と呼ばれる方々が、日夜そういう工夫を考えておられると思います。