2. "Implementing QuantLib"の和訳
Chapter-VII The Tree Framework: Tree を使った価格モデルのフレームワーク
7.2 Tree および Tree-Based Lattice
7.2.2 2項Treeおよび3項Treeクラス
既に触れた通り、Treeクラスにおける(Nodeの構造を管理する)インターフェースの実装方法は、実際の Node の配列を保持するか、それとも必要に応じて Node のインデックスを計算するだけにするか、のいずれかです。BinomialTreeクラステンプレートの実装内容を下記 Listing 7.8 に示しますが、後者の方法を取っています。見方によっては、各 Node がインデックスそのものと言えます。Node はインデックスとは別の存在とは言えません。(訳注:各離散時間のLevelにおける Node数は、再結合する 2項Tree の場合は、Levelが決まれば自動的に Node数も決まります。従って、あえて Node数を別の配列として持たなくとも個別の Node を特定可能です。一方で 3項Tree の場合は、各Levelにおける Node数は必ずしも決まっていません。従って、別途配列を保持する必要がある訳です)
Listing 7.8:BinomialTreeテンプレートクラス
template <class T>
class BinomialTree : public Tree<T> {
public:
enum Branches { branches = 2 };
BinomialTree(
const boost::shared_ptr<StochasticProcess1D>& process,
Time end, Size steps)
: Tree<T>(steps+1) {
x0_ = process->x0();
dt_ = end/steps;
driftPerStep_ = process->drift(0.0, x0_) * dt_;
}
Size size(Size i) const {
return i+1;
}
Size descendant(Size, Size index, Size branch) const {
return index + branch;
}
protected:
Real x0_, driftPerStep_;
Time dt_;
}; このクラステンプレートは様々な 2項Treeモデルの中で、特定のグループのものをモデル化しています。すなわち、確率変数のドリフト項と拡散項の係数が定数を取り、時間間隔は一定で、Tree が再結合するもののみを対象としています。(注: QuantLibライブラリーの“experimental”のフォルダーの中に、このクラスを拡張して、係数が定数でないもの(訳注:係数が時間の関数として決まるもの) を取り扱えるクラスを置いています。読者の方に見て頂き、フィードバックを頂ければうれしいです。ここでの説明では、係数が定数のバージョンだけを使います。)
そこまで限定したとしても、Tree を構築する方法には、さらにいくつかの選択肢があります。従って、大半の実装は派生クラスに任されています。このクラスはベースクラスとして、クラス全体で共通の機能を提供しています。最初に、branches という enum 変数が、定数=2 で設定されています。enum変数は、古いインターフェースに対応するメソッドを代替するものです。もし今なら、同じ目的のために、むしろ static const Size といった型のメンバー変数を使ったでしょう。Enumeration は、コンパイラーが標準に準拠していなかった時代の遺物と言えます。
コンストラクターは、引数として、①対象資産の変動を記述する1次元の確率過程 (StochasticProcess1Dインスタンス) への参照と、②Treeが扱う最終期日までの年数 (スタート日は0と仮定。これも内生的な定数)、③および離散時間のステップ数を取ります。また、いくつかのシンプルな事前計算を行いメンバー変数の値を設定します。すなわち、StochasticProcess1D の x0( ) メソッドを使って対象資産の初期値 x0_ を設定し、最終期日までの年数を Time Steps で割って時間間隔 (dt_) を計算し、そして時間間隔毎のドリフト項の値を、再び StochasticProcess1D インスタンスを使って計算します (ドリフト項の係数は定数なので、t=0 時点でのそれを計算しています)。これらの計算結果をそれぞれ各メンバー変数に代入します。
残念ながら、引数として与えられた StochasticProcess1D インスタンスが、定数係数の確率過程なのかどうか、確認する方法がありません。(訳注: 従って、上記のように、各Level間のドリフト項の値を、StochasticProcess1Dを使って t=0 から t=1 までの期間で計算し、それを他の期間にも援用していいのか、疑問。定数係数で無かった場合は、他の区間で、間違ったドリフト項の値を使う事になる) まず Library の中では、そもそも定数係数の確率過程の StochasticProcessクラス は宣言されていません。もしそうしようとすると、他の StochasticProcessクラスに対して、クラス階層上並列したものになるでしょう。そうすると、悪い意味での多重継承が発生します。例えば、“定数係数Black-ScholesProcessクラス”を宣言するとすれば、それは“定数係数Processクラス”と“Black-ScholesProcessクラス”の両方から継承する事になります。従って、(BinomialTreeクラスの)コンストラクターに渡す StochasticProcessクラスの型を(定数係数型に)制限して必要な型だけを取るようにする事はできません。また、実行時にその型をチェックする事もできません。いくつかの離散時間の時点をサンプルとして取りだし、チェックはできるでしょうが、他の時点もすべて定数である事を保証するものではありません。
(StochasticProcessクラスの型を間違えないようにする為に)残っているひとつの選択肢としては、この動作を文書化しておいて、ユーザーの方に間違った使い方をしないようにしてもらう事です。もうひとつの方法は コンストラクターに、StochasticProcessインスタンスを取らずに、定数係数を引数として取る事です(現時点では過去のバージョンとの互換性の為、そうする事を避けていますが、将来のバージョンアップの際に検討可能です) 。しかし、これはユーザーの方にコンストラクターを呼び出す都度、Processクラスから係数を取りだす作業を義務付けることになります。いつものように、バランスを考えて判断する必要があります。
最後の2つのメソッドは、Treeの構造を定義しています。size(i)メソッドは、i 番目のLevelの Node数 を返します。プログラムではレベル 0 すなわち Tree の根の部分は Nodeが1つと仮定しています。それは即ち、i 番目のレベルの Node数は、Nodeが再結合するので、常に i+1 になります。この想定は十分合理性のあるものと考えていましたが、Tree の開始時点が t=0 であると仮定している事と合わせて考えると、若干の問題に気付きました。まとめて申し上げると、この2つの前提により t=0 で Node を3つ持たせることができなくなり、その結果、差分による近似でデルタやガンマを計算する方法が取れなくなりました。幸いなことに、この問題は過去のバージョンとの互換性を失わせる事なく対応可能かと思います。もしユーザーの方がそれを実装しようとするなら、コンストラクターに追加の引数を加えるだけで、上記の仮定を緩める事ができ、そのテクニックを使えるようにできるでしょう。
最後に、descendant( )メソッドは、Node 間の接合を記述しています。Tree が単純な再結合の構造である為、あるLevelでインデックスが 0 の Node は、次のLevelのインデックス 0 と 1 の Node に接続します。インデックスが 1 の Node は次のLevelのインデックス 1 と 2 の Node に接続します。一般化すると、インデックスが i の Node は次のレベルのインデックス i と i+1 の Node に接続する事になります。どちらの Node に行くかは、メソッドに渡されるインデックス (2項Treeの場合は0か1) で決まるので、メソッドは単に、今のインデックスに渡されたインデックス(0か1)を加えるだけで行先を特定できます。いずれのインデックスも値の有効範囲の事前チェックは行われません。なぜならこのメソッドは常にループの中で呼び出されるので、チェックの動作自体が実行速度にマイナスに働くだけでなく (どの程度の影響があるかは、計測していませんので、そのままにしておきます)、ループを設定する際に同じ様な事が行われているので、実際にも余計なプロセスになります。
BinomialTree テンプレートクラスの実装では、対象資産の確率変動を、Tree の各 Node に対応させるメソッド、すなわち underlying( ) と probability( ) メソッドが定義されていません。これらのメソッドの実装方法は幾通りかあるので、派生クラスに任されています。実際に、そういった方法はいくつかのグループに分かれており、次の Listing 7.9 に示す Templateクラスのうち、最初の2つはそういったグループのベースクラスとする趣旨で実装されています。
Listing 7.9:BinomialTreeクラスの派生クラス
template <class T>
class EqualProbabilitiesBinomialTree : public BinomialTree<T> {
public:
EqualProbabilitiesBinomialTree(
const boost::shared_ptr<StochasticProcess1D>& process,
Time end, Size steps)
: BinomialTree<T>(process, end, steps) {}
Real underlying(Size i, Size index) const {
int j = 2*int(index) - int(i);
return this->x0_*std::exp(i*this->driftPerStep_ + j*this->up_);
}
Real probability(Size, Size, Size) const {
return 0.5;
}
protected:
Real up_;
};
template <class T>
class EqualJumpsBinomialTree : public BinomialTree<T> {
public:
EqualJumpsBinomialTree(
const boost::shared_ptr<StochasticProcess1D>& process,
Time end, Size steps)
: BinomialTree<T>(process, end, steps) {}
Real underlying(Size i, Size index) const {
int j = 2*int(index) - int(i);
return this->x0_*std::exp(j*this->dx_);
}
Real probability(Size, Size, Size branch) const {
return (branch == 1 ? pu_ : pd_);
}
protected:
Real dx_, pu_, pd_;
};
class JarrowRudd
: public EqualProbabilitiesBinomialTree<JarrowRudd> {
public:
JarrowRudd(
const boost::shared_ptr<StochasticProcess1D>& process,
Time end, Size steps, Real strike)
: EqualProbabilitiesBinomialTree<JarrowRudd>(process, end, steps) {
up_ = process->stdDeviation(0.0, x0_, dt_);
}
};
class CoxRossRubinstein
: public EqualJumpsBinomialTree<CoxRossRubinstein> {
public:
CoxRossRubinstein(
const boost::shared_ptr<StochasticProcess1D>& process,
Time end, Size steps, Real strike)
: EqualJumpsBinomialTree<CoxRossRubinstein>(process, end, steps) {
dx_ = process->stdDeviation(0.0, x0_, dt_);
pu_ = 0.5 + 0.5*driftPerStep_/dx_;
pd_ = 1.0 - pu_;
}
};
class Tian : public BinomialTree<Tian> {
public:
Tian(const boost::shared_ptr<StochasticProcess1D>& process,
Time end, Size steps, Real strike)
: BinomialTree<Tian>(process, end, steps) {
// sets up_, down_, pu_, and pd_
}
Real underlying(Size i, Size index) const {
return x0_ * std::pow(down_, Real(int(i)-int(index)))
* std::pow(up_, Real(index));
};
Real probability(Size, Size, Size branch) const {
return (branch == 1 ? pu_ : pd_);
}
protected:
Real up_, down_, pu_, pd_;
}; 最初に出てくる EqualProbabilitiesBinomialTreeクラスは、各 Node から同確率で2つに分岐する Tree 構造をモデル化したものです。この構造では probability( )メソッドの実装内容がそれぞれ 0.5 を返すように決まっていますが、一方で、underlying( )メソッドについては、制約がかかります。各分岐において同じ確率で分かれるという事は、Tree構造の中心ライン (各 Level における中心の Node )には、対象資産の価格の期待値が入る事を意味しています。言い換えると、各中心 Node には、その時点における対象資産のフォワード価格が入る事になります (下記の図の左側を参照下さい)。underlying( )メソッドの実装内容は、分岐先の対象資産価格の対数の平均が中心にくるような値を返します (プログラムコード全体がBlack-Scholes過程を念頭において書かれている事はお解りかと思います)。 メンバー変数 up_ の値は、各分岐における将来価格の、平均からの乖離幅として定義され、そのように使われています。下記の図での Δx がそれにあたります。しかし、コンストラクターの段階ではその値を設定していません。派生クラスに若干の柔軟性を与える為です。
<Equal-probabilities vs equal-jumps binomial trees.>
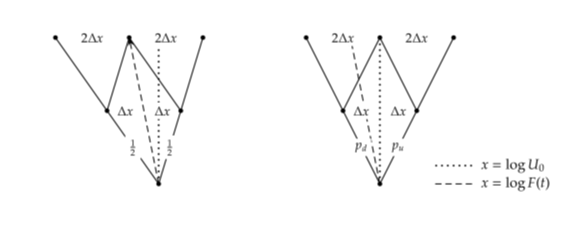
2番目の Template クラス、EqualJumpsBinomialTreeクラスは、分岐する際に、対象資産の価格の対数が、同じ変動幅で分かれるような Tree構造をモデル化したものです (上記の図の右側)。価格のドリフト部分が、分岐のどちらかに偏っている為、分岐の確率は左右で異なります。この Templateクラスは、underlying( )メソッドを、分岐がそうなる様に定義する一方、派生クラスにメンバー変数 dx_ の値を設定する作業を残しています。また probability( )メソッドはメンバー変数である pu_ か pd_ (upの確率とdownの確率)のいずれかの値を返す様に実装されていますが、それらの値は派生クラスで計算して設定されるようになっています。
最後に、上記 Listing で示している残りの3つのクラスは、いずれも実際に使われる具体的な2項モデルの例であり、従ってもはや Templateクラスではありません。最初のクラスは Jarrow-Rudd モデルを実装しています。このクラスは EqualProbabilitiesBinomialTreeクラスの派生クラスで (CRTPを使っている事に注目して下さい)、コンストラクターはメンバー変数 up_ の値を設定しています。その値は、1期間後の対象資産価格の分布における1標準偏差に相当するものです。次のクラスは、Cox-Ross-Rubinstein モデルを実装したもので、EqualJumpsBinomialTreeクラスの派生クラスになります。コンストラクターは、分岐の確率 ( pu_ と pd_ ) と中心値からの変動幅 (Δx) を計算します。3番目のクラスは、Tian モデルを実装したもので、上記の2つのベースクラスのいずれにも属さない例として示しています。その為、このクラスは BinomialTreeクラスから直接派生しており、必要なメソッドをすべてこのクラスで提供しています。
********************************************************************************
3項Treeモデルは、2項Treeとは全く異なったモデルとして実装されており、Node を繋ぐ方法は、はるかに柔軟です。その Tree 構造を構築する方法を、下記の図で示しています (より詳細な説明は Brigo Mercurio の著作[1]を参照)。Tree の各 Level において Node は等間隔で置かれており、その中心Nodeに設定される価格は、3項Treeの根にあたる Node (訳注:初期値) と同じ値に設定します。下記の図では \(A_3\) と \(B_3\) が中心Node に該当し、同じ垂直線上にあります。図をみれば判る通り、Levelが変わると、Nodeの間隔も異なります。
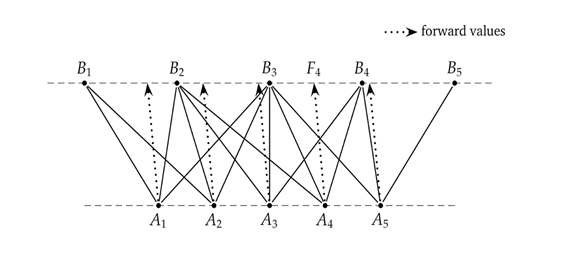
Nodeが設定されると、Node間の接続方法を構築していきます。同じ Level にある各 Node は、当然、その時点 t における対象資産の価値 x に対応しています。各Node において、StochasticProcessインスタンスを使えば、Node(x,t) から次の Level に遷移する際の条件付き期待値が求まります。上記の図における点線の矢印がそれに該当します。次の Level における、その将来価値(期待値)から最も近い Node を、3項Tree の分岐先の 中心Node とします。例えば、上の図の \(A_4\) の Node を見てください。対象資産の確率過程から計算された、将来価値の期待値は次のレベルの \(F_4\) になったとします。そこに一番近い Node は \(B_3\) になるので、\(A_4\) からの分岐は、\(B_3\) を中心として、その左隣りの \(B_2\) と右隣りの \(B_4\) に分かれていきます。
図から分かる通り、ある Levelの(隣り合う)2つの Node からみた、次のLevelにおける中心Node、すなわち将来価値に最も近いNodeが、同じになる事があり得ます。図では \(A_3\) と \(A_4\) の Node がいずれも \(B_3\) を中心Node として分岐しています。この事は、分岐元の各 Node からは、それぞれ3つに分岐する事は保証されていても、分岐先の Node においては、何か所の分岐元から遷移してきたかを前もって知ることがでません。上記の図では、\(B_5\) の分岐元は1つしかありませんが、\(B_3\) の分岐元は 5つの Node から来ています。それは、各 Level においていくつの Node が必要か事前には分からない事を意味しています。上の図のケースでは、Aのレベルの 5つの Node から分岐する先として、Bのレベルでは、Node が 5つで十分という事です。その数は、確率過程に依存し、より多くの Node が必要であったり、より少ない Node でもよかったりします (各Nodeの間隔を動かしてみて、実際にどうなるか試してみてください)。
今説明したロジックは、QuantLibライブラリーの TrinomialTreeクラス で実装されており、その内容を下記 Listing 7.10 に示します。
Listing 7.10:TrinomialTreeクラスの実装
class TrinomialTree : public Tree<TrinomialTree> {
class Branching;
public:
enum Branches { branches = 3 };
TrinomialTree(
const boost::shared_ptr<StochasticProcess1D>& process,
const TimeGrid& timeGrid,
bool isPositive = false);
Real dx(Size i) const;
const TimeGrid& timeGrid() const;
Size size(Size i) const {
return i==0 ? 1 : branchings_[i-1].size();
}
Size descendant(Size i, Size index, Size branch) const;
Real probability(Size i, Size index, Size branch) const;
Real underlying(Size i, Size index) const {
return i==0 ? x0_; x0_ + (branchings_[i-1].jMin() + index)*dx(i);
}
protected:
std::vector<Branching> branchings_;
Real x0_;
std::vector<Real> dx_;
TimeGrid timeGrid_;
}; コンストラクターは、引数として、①1次元の StochasticProcessクラスのインスタンス、②Tree の各 Level に対応する TimeGrid (時間間隔は等間隔である必要はありません)、および ③bool変数で確率変数の値が常に正であるべきかどうかを示すフラッグ、を取ります。
このオブジェクトの構築方法についてはすぐ後で説明しますが、その前に、Treeの構造に関する情報がどのように保持されているかについて説明する必要があります。即ち、インナークラスである Branching クラスについて説明する必要があります (その実装内容は下記 Listing 7.11 参照)。このクラスの各インスタンスは、1つのLevelのTree構造に関する情報を保持します。例えば、ひとつのインスタンスが、上記の図にあるようなNode間の関係性を保持します。
Listing 7.11:Implementation of the TrinomialTree::Branching inner class.
class TrinomialTree::Branching {
public:
Branching()
: probs_(3), jMin_(QL_MAX_INTEGER), jMax_(QL_MIN_INTEGER) {}
Size size() const {
return jMax_ - jMin_ + 1;
}
Size descendant(Size i, Size branch) const {
return k_[i] - jMin_ + branch - 1;
}
Real probability(Size i, Size branch) const {
return probs_[branch][i];
}
Integer jMin() const;
Integer jMax() const;
void add(Integer k, Real p1, Real p2, Real p3) {
k_.push_back(k);
probs_[0].push_back(p1);
probs_[1].push_back(p2);
probs_[2].push_back(p3);
jMin_ = std::min(jMin_, k-1);
jMax_ = std::max(jMax_, k+1);
}
private:
std::vector<Integer> k_;
std::vector<std::vector<Real> > probs_;
Integer jMin_, jMax_;
}; すでに述べた通り、各 Node は対象資産の初期値に対応する‘中心Node’を基準にして位置を決めます。理由は、Tree の各 Level で (事前に) Node数がいくつになるか判らないので、それ(初期値を基準にした中心Node) しか基準となるポイントが無いからです。従って、Branchingクラスは中心 Node のインデックス j を 0 とし、そこから外に向かって(訳注:同じ Level 上で、確率変数の値が拡散する両方向に向かって)インデックス番号を付けています。例えば、前に示した Tree の図の下側の Level上の Node で言えば、\(A_3\) にインデックス j=0 を対応させ、\(A_4\) が j=1、\(A_2\) が j=−1 とします。上側の Level では \(B_3\) が j=0 に対応します。このインデックスを Tree のインターフェースで使われているインデックスに変換する必要があります。なぜならTree のインデックスは、図の一番左の Node( \(A_1\) ) のインデックスが 0 になるからです。
Tree構造に関する情報を保持する為、Branchingクラスは以下のメンバー変数を保持します。
1. 整数の配列で、分岐元の各Node に対応する、分岐先の中心 Node インデックスを格納。(左右の分岐先の Node を保持する必要はありません。なぜなら、それは必ず中心 Node の両隣だからです)
2. 3つの配列。データアクセスが便利なように、配列の配列として宣言されている。それぞれ、各 Node における分岐先への遷移確率を格納。
3. 2つの整数。分岐先 Level における Nodeインデックスの最小値と最大値を保持。
Treeクラスのインターフェースを実装する際、数種類のインデックスをうまく扱わないといけないので、注意が必要です。例えば、TrinomialTree のコードに戻って size( )メソッドを見てください。このメソッドはレベル i (訳注: i 番目の時間軸) における Node数を返します。しかし、(TrinomialTreeインスタンスではなく) 各 Branching インスタンスが、自分の分岐先の Node に関する情報を持っているので、正しい数は branchings_[i-1] から取りださなければなりません。 (但し i=0 の場合だけは、最初から 0 (訳注: 1 の間違いだと思います) と決まっているので、その値を返します。) この動作の為に、Branchingクラスでは、分岐先 Level の Node数を返す size( )メソッドを用意しています。jMax_ と JMin_ の変数に、それぞれ左右の両端のインデックス番号を保持しているので、size( )メソッドが返す値は、jMax_− jMin_ + 1 になります。上記の図ではインデックスは -2 から +2 (\(B_1\) から \(B_5\) に対応)なので Node数は 5 になります。
TrinomialTreeクラスの descendant( )と probability( )メソッドは、いずれも Branchingクラスが持つ対応するメソッドを呼び出します。descendant( )メソッドは分岐元の i 番目の Node から、分岐先Node のインデックス番号を返します (引数の branch で取る 0 か 1 か 2 の数字が、それぞれ分岐先の左、真ん中、右を指定します)。そうするには、そのメソッドは最初に、分岐先の 中心Node のインデックスを示す k を、内部のインデックス体系から取りだします。そして、その数字から jMin を引くと、対応する外部の Nodeインデックスに変換され(訳注: 外部のNodeインデックスは、各Levelの最も左側のインデックスを 0 とし、そこから1,2,..と付番されており、その体系に変換される)、最後に、その数字に branch – 1 (引数として取った分岐先のインデックスから 1 を引いた値。従って -1 か 0 か 1)を加えると、分岐先 Tree上の Nodeインデックス番号が得られます。probability( )メソッドの内容は簡単です。各 Nodeに対応する分岐先への遷移確率の情報を、Nodeインデックス i を指定して配列変数から取りだすだけです。その配列変数のインデックスは 0 を基準点としているので、インデックスの変換は必要ありません。
最後に、underlying( )メソッドはTrinomialTreeクラスで直接実装されています。なぜなら、Branchingインスタンスは、必要なStochasticProcessインスタンスの情報を持っていないからです。Branchingクラスは、インスペクター関数であるjMin( )メソッドを提供しており、TrinomialTreeクラスはそれを使って、センターNodeから最も左側のNodeまでのインデックス番号の差を計算します。BranchingクラスはjMax( )というインスペクター関数とadd( )メソッドも提供しています。後者のメソッドは分岐を構築して行くのに使われます。このメソッドの名前は、push_backを使った方が良かったかも知れません(訳注:メソッドの動作が、算術的な加算をしているのではなく、配列の要素数を増やしているため)。このメソッドは、引数として渡されたデータ(中心Nodeのインデックスと、3つの分岐確率)を、それぞれ対応する配列要素に加えます。また、最小インデックスと最大インデックスの情報の更新も行います。
残った説明は、どのようにして TrinomialTree のインスタンスを構築するかを示す事です (説明には下記 Listing 7.12 と、既に何度も説明に使った3項Tree の分岐図を使います)。
Listing 7.12: TrinomialTreeインスタンスの構築
TrinomialTree::TrinomialTree(
const boost::shared_ptr<StochasticProcess1D>& process,
const TimeGrid& timeGrid, bool isPositive)
: Tree<TrinomialTree>(timeGrid.size()), dx_(1, 0.0), timeGrid_(timeGrid) {
x0_ = process->x0();
Size nTimeSteps = timeGrid.size() - 1;
Integer jMin = 0, jMax = 0;
for (Size i=0; i<nTimeSteps; i++) {
Time t = timeGrid[i];
Time dt = timeGrid.dt(i);
Real v2 = process->variance(t, 0.0, dt);
Volatility v = std::sqrt(v2);
dx_.push_back(v*std::sqrt(3.0));
Branching branching;
for (Integer j=jMin; j<=jMax; j++) {
Real x = x0_ + j*dx_[i];
Real f = process->expectation(t, x, dt);
Integer k = std::floor((f-x0_)/dx_[i+1] + 0.5);
if (isPositive)
while (x0_+(k-1)*dx_[i+1]<=0)
k++;
Real e = f - (x0_ + k*dx_[i+1]);
Real e2 = e*e, e3 = e*std::sqrt(3.0);
Real p1 = (1.0 + e2/v2 - e3/v)/6.0;
Real p2 = (2.0 - e2/v2)/3.0;
Real p3 = (1.0 + e2/v2 + e3/v)/6.0;
branching.add(k, p1, p2, p3);
}
branchings_.push_back(branching);
jMin = branching.jMin();
jMax = branching.jMax();
}
} 2ページほど前にあった Code Listing のとおり、このクラスのコンストラクターは、対象資産の確率過程を記述する StochasticProcess と、TimeGrid、および bool変数を取っていることが分かります。TimeGrid における Grid数が、TrinomialTree における Level数に対応します。従って、その情報はベースクラスのコンストラクターに渡されます。また TimeGridインスタンスはメンバー変数に保存され、各 Level における Node間隔を示す dx_ の配列が初期化されます。最初の Level(t=0) の Node数は 1 なので、Node間の距離は存在せず、dx_ 配列の最初の要素には 0 が代入されます。コンストラクターが行うその他の準備作業は、対象資産価格の初期値 x0_ や、離散時間のステップ数をメンバー変数に保存する事です。さらに、2つの変数 jMin と jMax を宣言し、Node のインデックス番号の最小値と最大値を代入します。最初の Level では、いずれも 0 で設定されます。(訳注: 以上のプロセスは、上記Code Listingの Integer jMin=0, jMax=0; の所まで)
この準備作業の後、Tree構造が Level毎に順番に構築されていきます。各ステップにおいて、TimeGrid インスタンスからステップ開始時 t とステップ間隔 dt を取りだします。この情報を使って、Processインスタンスから、その間隔に対応する分散の値を取りだします。この分散の値は、確率変数の値からは独立と仮定しています ( 2項Tree では、これを強制する方法はありません)。分散の値を基に、次の Level の Node間隔を計算し、それを dx_ の配列に保持します (注: Hull-Whiteによれば分散値の \(\sqrt 3\)倍が、最も安定的な Tree構造を構成すると言われています。[訳注: 原著では分散の \(\sqrt 3\) 倍と書かれていますが、標準偏差の \(\sqrt 3\) 倍の間違いだと思います。Code の方はそうなっていまず] )。その後で、最後に Branching インスタンスを生成します。(訳注:上記 Code Listingの Branching branching; まで)
ここからのプロセス ( 訳注:上記Code Listing の inner for ループの内容のこと) をイメージするため、先ほどの図に戻って下さい。プログラムコードは、下の Levelの各 Node をループします。Node のインデックス番号は現時点の (訳注:outer for ループが Level毎に更新しているが、その直近の) jMin と jMax の間の値を取ります。 図のケースでは \(A_1\) が −2、\(A_5\) が +2 に該当します。そして、まず各 Node における対象資産の値 x を、初期値 x0 とインデックス番号 j および Node間隔 dx_[i] を使って計算します。次に、その x の値から StochasticProcessインスタンスを使って、dt 後の将来価値 f を導出します。そして、次の Level の Node間隔 dx_[i+1] を計算した後、次の Level における、f に最も近い Nodeインデックスを探します。それを k と置きますが、k は内部インデックスです。(訳注: TrinomialTreeクラスにおいては、センターNode のインデックスを 0 として、その外側に向けて、jMax、...+1、+2、.. −1, −2,... jMin とインデックス番号を付けている。それを内部インデックスと呼んでいる。それに対し、ベースクラスの Treeクラスでは、インデックスは一番低い方から 0,1.2,… と付番されている。) 図の \(A_4\) の Node に対応する将来価値は \(F_4\) になりますが、そこに最も近い\(B_3\) が (\(A_4\) の分岐先の) 中心 Node となり、そのインデックス番号は k=0 となります。
bool変数 isPositive が True に設定されている場合、マイナス値またはゼロ値の入っている Node を分岐先として使わないようにする為に、中心 Node の左側の Node (インデックスで言えば k-1。中心 Node のインデックスが k=0 である為) に設定されている対象資産の値をチェックし、その値が正でなければ k の値を 1 増やします。そのステップを左側の Node の値が正になる所まで繰り返します。前の図で言えば、Node \(B_1\) に格納されている値が負であれば、Node \(A_1\) の分岐先は \(B_2、B_3、B_4\) に変更されます。
最後に、3つの分岐先への遷移確率 p1、p2、p3 を計算し (プログラムコード中の各確率の計算式は Brigo-Mercurioの下記[1]を参照)、その値をBranchingインスタンスのメンバー変数に、kと共に保存します。すべてのNodeでこのプロセスが終わると、Branchingインスタンスを保存し、上のレベル(分岐先のレベル)に合わせたjMinとjMaxの値をアップデートします。その値は、外側のforループ(Time Stepsの数だけループしている部分です)の次のサイクルで、Levelを1つすすめた所で使われます。
[1] D. Brigo and F. Mercurio, Interest Rate Models − Theory and Practice, 2nd edition. Springer, 2006.
<ライセンス表示>
QuantLibのソースコードを使う場合は、ライセンス表示とDisclaimerの表示が義務付けられているので、添付します。 ライセンス