2. "Implementing QuantLib"の和訳
Chapter VIII The Finite-Difference Framework (有限差分法のフレームワーク)
8.1 The Old Framework (古いフレームワーク)
8.1.6 Example: American Option (具体例 アメリカンオプション)
ここまでくれば、有限差分法を使った価格エンジンのプログラムコードを書くのは、きっと、点と点をつなぐだけになるはずです。と言いたいところですが、そうでもありません。このセクションンでは、QuantLibにある、アメリカンオプション価格エンジンの実装方法を概観しますが、その中味は、予想したよりも複雑です。(次のチャート図を見ればわかる通りです)
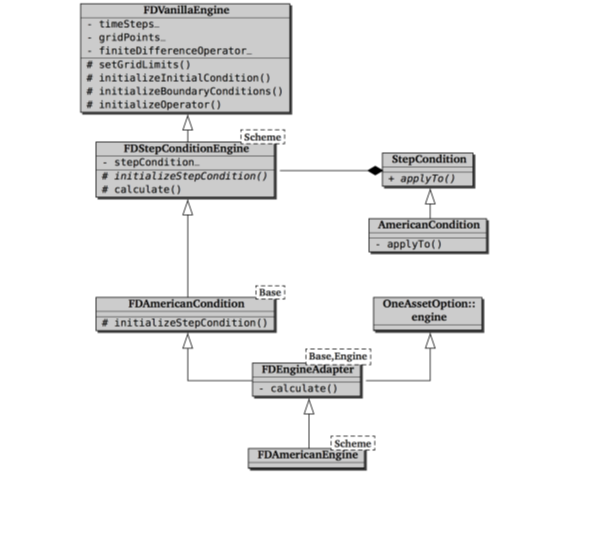
このチャート図を作った理由は2つあります。ひとつは、このChapterを書くにあたって、この価格エンジンのコードを見直したところ、自分でさえどこにいるか迷ってしまいそうになった事です。それで、全体の構成を図にまとめるのは役に立つであろうと考えました。もうひとつは、この例を使って、新しい(そしてよりモジュール化された)フレームワークと比較するのに役立つと考えた事です。
注意しておきますが、私は古いフレームワークの実装方法を批判しているのではありません。古いフレームワークが、これほどまでに複雑になってしまったのは、再利用可能なプログラムコードを、できるだけ抽象化しようとした為です。抽象化自体は意味のある事です。問題は、開発時は判らなかったのですが、抽象化のために‘継承’を使ったのは、おそらく間違ったやり方でした。
では、FDVanillaEngineクラスから始めましょう。そのコードを下記Listing 8.10に示します。このクラスは、Vanilla Optionや Dividend Vanilla Optionエンジンのベースクラスになります。クラス名を FDVanillaOptionEngine のように、より詳しい名前にしなあったのは、その為です。(いや、ただ単に名前を短くしようとしただけかもしれません。開発後、何年も経っているので、だれも覚えていません)
Listing 8.10:FDVanillaEngineクラスのインターフェース
class FDVanillaEngine {
public:
FDVanillaEngine(
const shared_ptr<GeneralizedBlackScholesProcess>&,
Size timeSteps, Size gridPoints,
bool timeDependent = false);
virtual ~FDVanillaEngine() {}
protected:
virtual void setupArguments(
const PricingEngine::arguments*) const;
virtual void setGridLimits() const;
virtual void initializeInitialCondition() const;
virtual void initializeBoundaryConditions() const;
virtual void initializeOperator() const;
shared_ptr<GeneralizedBlackScholesProcess> process_;
Size timeSteps_, gridPoints_;
bool timeDependent_;
mutable Date exerciseDate_;
mutable boost::shared_ptr<Payoff> payoff_;
mutable TridiagonalOperator finiteDifferenceOperator_;
mutable SampledCurve intrinsicValues_;
typedef BoundaryCondition<TridiagonalOperator> bc_type;
mutable std::vector<boost::shared_ptr<bc_type> > BCs_;
virtual void setGridLimits(Real, Time) const;
virtual Time getResidualTime() const;
void ensureStrikeInGrid() const;
private:
Size safeGridPoints(Size gridPoints,
Time residualTime) const;
}; このクラスは、有限差分モデルで必要な部品のほとんどを、コンストラクターに渡された引数をもとに、作成します。その引数とは、①対象資産の Black-Scholes過程(インスタンスへのポインター)、②時間軸のステップ数、③状態変数の格子の数、および④フラッグ(これについては次のセクションまで無視します)です。引数として渡された入力項目以外に、メンバー変数には、Instrumentインスタンスから取りだした、オプション商品に関する情報や(行使日とPayoff)、構築される有限差分モデルの部品(すなわち、差分演算子、境界条件、およびpayoffの行使価値に対応する初期条件の配列)も含まれています。初期条件の配列(満期payoffのデータ)は、SampledCurveクラスのインスタンスの中に保存され、そのクラスはデータアクセス用の utilityメソッドを提供しています。
このクラスの残りのメソッドは、protectedとして宣言されており、メンバー変数を生成したり、それを使った計算を行なったりします。それらを簡単に見ていきましょう。詳細な実装内容は、Libraryの中のコードを直接ご覧下さい。
最初に、恐ろしく間違った名前をつけられたsetupArguments( )メソッドですが、このメソッドの動作は、Instrumentクラスの同じ名前のメソッドと全く逆の事を行います。すなわち、引数として取られたarguments構造体から、計算に必要なオプション行使の条件とPayoffの条件を読み取り、それをFDVanillaEngineのメンバー変数にコピーしています。
setGridLimits( )メソッドは、引数として渡された確率過程オブジェクトを使って、オプション行使期限までの“分散”の値を計算し、それを基にモデルの状態変数軸(対数値)の、最小値と最大値を決め、それをメンバー変数に保存します。その計算過程において、対象資産の現時点の価格(の対数)が、格子の中心に来るようにし、かつ行使価格がレンジの中に必ず入るようにし、さらに格子の数が十分大きな数になるようにします。(注:このメソッドはユーザーが引数で設定した格子数を、(格子数を十分大きくする為に)後から勝手にオーバーライドする可能性があります。後から見ると、ユーザーに知らせる事無くそれを行うのがよかったのか自信がありません) 実際の動作は、いくつかの他のメソッド(オーバーロードされた同じsetGridLimits( )、 safeGridPoints( ) およびensureStrikeInGrid( ) )に委託されています。
initializeInitialCondition( )メソッドは、新しく生成された格子上の(対象資産価格から)Payoffを計算し、満期時のオプション行使価値の配列を設定します。従って、このメソッドはsetGridLimits( )メソッドの後に呼び出さなければなりません。
次のステップで呼び出される initializeBoundaryConditions( )メソッドは、上界と下界の境界条件の設定を行います。いずれの境界条件もノイマン条件で、境界で設定されるオプション価格はオプション行使価値の配列をベースに数値的に計算されます (訳注:ノイマン条件は境界における1階微分の値が条件として与えられるので、境界近辺のグリッド間の差分を使って、条件にフィットする境界値を設定する)。
最後に、initializeOperator( )メソッドは、グリッド数と確率過程オブジェクトを使って、TridiagonalOperator(三重対角演算子)オブジェクトを生成します。このメソッドも、実際の計算を他のインスタンス(このケースでは OperatorFactoryクラスのインスタンス)に委託していますが、このクラスについては後程説明します。
以上のメソッドはすべて仮想関数として宣言されており、必要があれば、デフォールトの実装内容をオーバーライドできます。でも、この方法は最適ではありません。メソッド内のロジックを少しでも変更しようとすると、それだけの為に継承を使う必要があります。そうするとユーザーによるカスタマイズの為だけに新たなクラス概念を導入する事になり、別のタイプの変更に対応できません。ここでは、Strategyパターンを使う方が良かったかも知れません。そうすればロジックの一部を他の商品で再利用する事ができました。
結局の所、いろんな問題はあるものの、なんとかなります。下記の Listing 8.11にある FDEuropeanEngineクラスのように、ある程度合理的な量のプログラムコードで、(機能する価格エンジンが)実装可能です。calculate( )メソッドは、FDVanillaEngineクラスから適当なメソッドを呼び出して、必要なセットアップをすべて行い、オプション期日における行使価値からスタートして、評価日(=現在)まで時間を遡って有限差分モデルを生成します。オプション価格と、2種類の Greeks(パラメータに対する価格感応度。ここではデルタ(Δ)とガンマ(Γ))は、SampledCurveクラスの対応するメソッドを使って取りだす事が出来ます。さらに、シータ(θ)の値は Black-Scholes方程式によって規定されるシータと他の数値との関係から計算できます。(注:Black-Scholes方程式の偏微分項を、対応するGreeks(θ、Γ、Δ)で置き換えると次のようになります。 \( θ+1/2 σ^2 S^2 Γ+(r-q)S Δ-rV=0 \) この式に、オプション価格 V と SampledCurveから求まった Γ と Δ を代入すれば、残りの未知数 θが求まります。)
Listing 8.11:FDEuropeanEngineクラスの実装内容
template <template <class> class Scheme = CrankNicolson>
class FDEuropeanEngine : public OneAssetOption::engine,
public FDVanillaEngine {
public:
FDEuropeanEngine(
const shared_ptr<GeneralizedBlackScholesProcess>&,
Size timeSteps=100, Size gridPoints=100,
bool timeDependent = false);
private:
mutable SampledCurve prices_;
void calculate() const {
setupArguments(&arguments_);
setGridLimits();
initializeInitialCondition();
initializeOperator();
initializeBoundaryConditions();
FiniteDifferenceModel<Scheme<TridiagonalOperator> >
model(finiteDifferenceOperator_, BCs_);
prices_ = intrinsicValues_;
model.rollback(prices_.values(), getResidualTime(),
0, timeSteps_);
results_.value = prices_.valueAtCenter();
results_.delta = prices_.firstDerivativeAtCenter();
results_.gamma = prices_.secondDerivativeAtCenter();
results_.theta = blackScholesTheta(process_,
results_.value,
results_.delta,
results_.gamma);
}
}; 先ほどのチャート図の関係はどうなっているのでしょう? すなわち、FDVanillaEngineクラスから FDAmericanEngineクラスまでの3段階にも渡る継承は、どうなっているのでしょうか? このような多重の階層構造にしたのは、再利用できるロジックの部分はできるだけそうしたかったからです。既に述べた通り、考え方は正しかったと思います。QuantLibライブラリーの中で、このコードの一部を再利用しているオプション(shout optionや、配当CFを離散的に取り扱うOptionモデルなど)もあります。(いずれにしても)この構造は、改良可能でした。
まず(FDVanillaEngineから派生する第1段階として)、次の Listing 8.12に示す、FDStepConditionEngineクラスの概要を見て下さい。
Listing 8.12:FDStepConditionEngineクラスの概要
template <template <class> class Scheme = CrankNicolson>
class FDStepConditionEngine : public FDVanillaEngine {
public:
FDStepConditionEngine(
const shared_ptr<GeneralizedBlackScholesProcess>&,
Size timeSteps, Size gridPoints,
bool timeDependent = false);
protected:
// ...data members...
virtual void initializeStepCondition() const = 0;
virtual void calculate(PricingEngine::results*) const {
OneAssetOption::results * results =
dynamic_cast<OneAssetOption::results *>(r);
setGridLimits();
initializeInitialCondition();
initializeOperator();
initializeBoundaryConditions();
initializeStepCondition();
typedef /* ... */ model_type;
prices_ = intrinsicValues_;
controlPrices_ = intrinsicValues_;
// ...more setup (operator, BC) for control...
model_type model(operatorSet, bcSet);
model.rollback(arraySet, getResidualTime(),
0.0, timeSteps_, conditionSet);
results->value = prices_.valueAtCenter()
- controlPrices_.valueAtCenter()
+ black.value();
// same for Greeks
}
};このクラスは、各Stepにおける計算の都度 Step Conditionが適用になる有限差分モデルの価格エンジンとなります。この中の calculate( )メソッドの中で、価格計算のロジックの主要部分を実装し、さらに Greeksの計算も行っています。その動作内容は、
- まず、FDVanillaEngineベースクラスから継承したメソッド群を呼び出し、メンバー変数を設定します。
- 同時に、このベースクラス内で純粋仮想関数として宣言されている(従って派生クラスで実装する必要がある) initializeStepCondition( )メソッドを呼び出します。このメソッドは、与えられた価格エンジンに対応する StepConditionのインスタンスを生成しなければなりません。
- 次に、2種類のデータ配列を生成します。一つは計算しようとしているオプション価格のデータ用、もうひとつは制御変数として使われるヨーロピアンオプションの価格用です。(制御変数との誤差を計算する為、ヨーロピアンオプション用の差分演算子のセットアップと、Black解析解を実装する価格エンジンが必要になります。)
- その後、有限差分モデルのインスタンスが生成され、両方の配列に作用させます。その際、Step Conditionは前者にのみ適用されます。
- 最後に、前者の計算結果を、後者の制御変数の計算結果を使って修正します。
このクラスからは、特に強調すべき重要なポイントはありませんが、クラス名については、汎用的すぎるかと思います。制御変数の使用について、ひとつだけ説明を加えます。制御変数を使うテクニックについては Chapter-VI で既に見てきました。そこではシミュレーションされた価格の分布を狭める為に使われていました。ここでは、数値計算の精度を上げる為に使われています。現時点では、このテクニックの使用を有効にしたり無効にしたりできるフラッグの設定が為されていない為、使用をユーザーに強制する形になっています。一方で、モンテカルロシミュレーションと異なり、制御変数を使うテクニックは有限差分スキームの計算時間速度に大きな影響を与えます。(モンテカルロシミュレーションでは、計算時間の大半を Pathの生成に使い、そのPathはオプション価格の計算と制御変数の計算でシェアされますが、有限差分法では、制御変数を使う事で、計算時間がほぼ2倍になります。) このテクニックを使うかどうかの判断は、おそらくユーザーに委ねられるべきだったかもしれません。また、制御変数のデータの為に mutableなメンバー変数を宣言するのでは無く、一時変数を使うべきでした。安易に mutableなメンバー変数を使うのは、悪い癖になります。
次は (FDVanillaEngineから派生する第2段階である) FDAmericanConditionクラステンプレートの説明です。下記 Listing 8.13をご覧下さい。このクラスは、ベースクラスを Template引数として取り (このケースではFDVanillaEngineクラスになります)、initializeStepCondition( )メソッドを実装しています。このメソッドは、AmericanConditionオブジェクトを返します(訳注:Listingにあるインターフェースを見る限り、このメソッドのreturn値はvoidになっています。ソースコードを見ると、メソッド内でAmericanConditionオブジェクトを生成し、FdVanillaEngineクラスのstepCondition_メンバー変数に代入しています)。残念ながら、FDAmericanConditionというクラス名は、すごく混乱させる名前です。名前からすると、このクラスは、Pricing Engineの為の構成部品というよりは、Step Conditionの派生クラスに見えてしまいます。
Listing 8.13:FDAmericanEngineクラスとその直接の派生元となるベースクラスの概要
template <typename baseEngine>
class FDAmericanCondition : public baseEngine {
public:
FDAmericanCondition(
const shared_ptr<GeneralizedBlackScholesProcess>&,
Size timeSteps = 100, Size gridPoints = 100,
bool timeDependent = false);
protected:
void initializeStepCondition() const;
};
template <typename base, typename engine>
class FDEngineAdapter : public base, public engine {
public:
FDEngineAdapter(
const shared_ptr<GeneralizedBlackScholesProcess>& p,
Size timeSteps=100, Size gridPoints=100,
bool timeDependent = false)
: base(p, timeSteps, gridPoints,timeDependent) {
this->registerWith(p);
}
private:
void calculate() const {
base::setupArguments(&(this->arguments_));
base::calculate(&(this->results_));
}
};
template <template <class> class Scheme = CrankNicolson>
class FDAmericanEngine
: public FDEngineAdapter<
FDAmericanCondition<
FDStepConditionEngine<Scheme> >,
OneAssetOption::engine> {
public:
FDAmericanEngine(
const shared_ptr<GeneralizedBlackScholesProcess>&,
Size timeSteps=100, Size gridPoints=100,
bool timeDependent = false);
}; 次の派生段階は、上記 Listingにある FDEngineAdapterクラステンプレートです。このクラスは“実装”と“インターフェース”を結びつける役割を負っています。すなわち両者の役割を担うクラスをそれぞれ Template引数として取っています。このケースでは、FDAmericanConditionクラスが“実装”を担い、OneAssetOption::engineが”インターフェース”を担っています。このクラスはまた、calculate( )メソッドの中で glue codeを提供しており、そのメソッドが“実装”のメソッド群を呼ぶに事よって、価格エンジンの“インターフェース”の役割を満たしています。(訳注:価格エンジンのインターフェースとなる calculate( )メソッド内で、FDAmericanConditionクラスで実装されているメソッドを呼び出す事により、両方のベースクラスを接着している)
最後の、FDAmericanEngineクラスは、FDEngineAdapterクラスから派生し、Template引数のクラスを具体的に特定したものです。
問題は、ベースクラスのコードのわずかな部分を再利用する為に、階層構造の複雑さを増す事が見合うかどうかです。私自身、答えられる確信がありませんが、別の方法での実装方法を示す事が出来るので、読者自身で比較できるようにします。仮に、FDAmericanEngineクラスを、FDStepConditionクラスと OneAssetOption::engineクラスから直接派生させ、中間にあったFDAmericanCondition と FDEngineAdapterクラスで記述されたコードを、ここに移したとすると、次の Listing 8.14に示すような実装内容になります。
Listing 8.14 : FDAmericanEngineクラスの別の実装方法
template <template <class> class Scheme = CrankNicolson>
class FDAmericanEngine
: public FDStepConditionEngine<Scheme>,
public OneAssetOption::engine {
typedef FDStepConditionEngine<Scheme> fd_engine;
public:
FDAmericanEngine(
const shared_ptr<GeneralizedBlackScholesProcess>& p,
Size timeSteps=100, Size gridPoints=100,
bool timeDependent = false)
: fd_engine(p, timeSteps, gridPoints, timeDependent) {
this->registerWith(p);
}
protected:
void initializeStepCondition() const;
void calculate() const {
fd_engine::setupArguments(&(this->arguments_));
fd_engine::calculate(&(this->results_));
}
} 私の個人的な意見ですか? 年を取ってくると、単純な方に傾きがちです。複製されるプログラムコードが殆ど無く、それを再利用するクラスの数も多くありません(現バージョンの QuantLibライブラリーの中で、約半ダース程度)。さらに、取り除かれるクラス (FDAmericanConditionクラスとFDEngineAdapterクラス)は、実際のところ、ドメインの中で何等かの概念をオブジェクトモデル化したものではありません。すなわち、それらを取り除く事に特に不安はありません。適切な抽象化が為されないまま再利用をし過ぎる事は、結局問題かもしれません。
最後の注意点です。ご覧の通り、このフレームワークの中では、広範なオプションモデルの動作をカプセル化した、ハイレベルのクラス(モンテカルロフレームワークではMcSimulationクラスが該当。6.3参照)は存在していません。ここで示した各クラスの中に書きこまれているロジック(有限差分のアルゴリズム)は、1種類の商品、すなわちBlack-Scholes-Mertonモデルを使ったプレインバニラのオプションのみ対象としています。
<ライセンス表示>
QuantLibのソースコードを使う場合は、ライセンス表示とDisclaimerの表示が義務付けられているので、添付します。 ライセンス