1. QuantLibを使ってみる
1.2 Exampleを試す
1.2.4 Bonds : 債券オブジェクトの構築と価格計算
1.2.4.1 はじめに
このExampleでは、一般的な債券の、価格、利回り、経過利息などを計算します。債券利回りの計算は、市場慣行では内部収益率(IRR : Internal Rate of Return)を使うのが一般的です。内部収益率は、金利の期間構造を考慮しませんが、逆に1個の値で利回りを表現できるので、期間の異なる債券の利回りを比較するのには便利です。また、債券利回りからの価格計算も、市場慣行ではイールドカーブの構築を必要としないので、はるかに簡単です。
しかし、このExampleでは、債券価格を、イールドカーブを構築して、期間構造も勘案した上で計算しています。そもそも債券は、始めに市場価格ありきで、その市場価格データからイールドカーブを構築するので、前後が逆の様にみえます。しかし、デリバティブズが付随した仕組債券などは、イールドカーブと、価格モデルを使って価格計算を行う必要があります。この例を使って、ベンチマーク債券の市場価格からイールドカーブを構築する方法と、一般的な債券オブジェクトの構築方法、さらに価格エンジンを設定して価格計算する方法を見ていきたいと思います。さらに、参考の為に、債券の市場価格から、市場慣行による利回り計算や、経過利息計算も行っています。
これまでの例と同様、”Bond”という Financial Instruments(金融商品オブジェクト)と、債券用の Pricing Engine(価格エンジン)を構築し、両者を組みあせて、価格計算を行います。価格計算にイールドカーブを使うので、その構築にテストコード全体の半分以上を費やしています。債券価格の計算に、イールドカーブを使うケースは、債券にデリバティブズが組み込まれた仕組み証券などで想定されます。その場合、組み込まれているデリバティブズに合わせたPricing Engineが必要になります。しかしこの例では、特にそういった債券の価格評価をしている訳ではなく、使われているPricing Engineはシンプルで、イールドカーブからDiscount Factorを導出し、キャッシュフローの現在価値を計算しているだけです。
デリバティブズ用のPricing Engineを使った、コールオプション付き債券の価格計算は、次のCallableBondsのExampleで解説します。
1.2.4.2 ソースコードのコンパイルと実行
これまでの2例と同様、まずExampleのソースコードをビルドし、実行可能なバイナリーファイルを生成します。 QuantLibのインストール方法を解説したセクションですでにビルドしていれば、再ビルドは必要ありません。もし、ビルドが済んでいない場合は、次の手順で、Debugモードでビルドし、試しに実行してみて下さい。
- QuantLibのファイルFolderのExampleディレクトリから、Bondsのディレクトリを探し、そこにあるプロジェクトファイル bonds.vcxproj をダブルクリックし開ける。Visual Studio が起動され、このプロジェクトファイルが開かれます。
- ソリューションエクスプローラーに表示されているプロジェクトのディレクトリを展開し、SourceFiles のフォルダーにある "bonds.cpp" をクリックする。約590行あるソースコードが開かれます。
- きちんと動作するか、まず確認してみます。まずメニューバーからビルド→ソリューションのビルドを選択。ビルドが開始されます。既にビルド済みであれば、この操作は必要ありません。(当初、複数のプロジェクトをまとめているQuantLib.slnをビルドした場合、個別のプロジェクトにおけるmain()関数を走らせる必要があります。その場合は、ソリューションエクスプローラーwindowから、該当のプロジェクト(ここではbonds.)をクリックした上で、メニューバーから “プロジェクト” → “スタートアッププロジェクトに設定” を選択して下さい。)
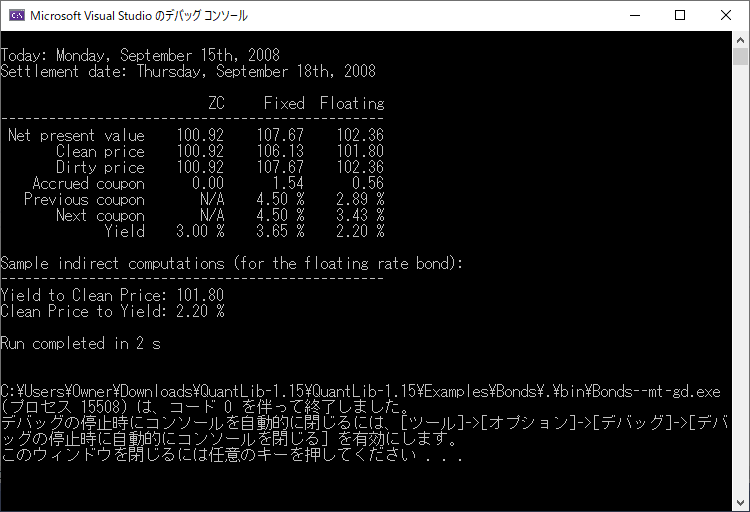
- エラー無くビルドが正常終了すれば、試しにプログラムを走らせてみます。メニューバーのデバック→デバックの開始を選択。下記の Console画面が出力されれば成功です。(但し、プログラムが終了すると同時に Console画面も消えてしまうようであれば、メニューバーから、 ツール → オプション → デバック → 全般 を選択し、「デバックの停止時に自動的にコンソールを閉じる」のチェックボックスをはずします。)
- 出力結果を見れば判る通り、この例では、ゼロクーポン債、固定金利債、変動利付債の3種類の債券について、NPV (正味現在価値)、Clean Price(経過利息を含まない債券価格)、Dirty Price(経過利息分を含めた債券価格)、経過利息相当額、前回クーポンレート、次回クーポンレート、最終利回り、を計算し出力しています。また、最後に変動金利債の価格と利回りを、期間構造を考えない市場慣行に則った方法でも計算しています。
1.2.4.3 ソースコードの解析
< 全体像 >
まず、ソースコード全体を俯瞰してみます。(参考のために、ソースコード(bonds.cpp ファイル)を .html ファイルに変換したものを、用意したので、それを見ながら読み進めて下さい。)
bonds.cppのプログラムコードは、全体で約590行あります。その内、約300行を、イールドカーブの構築に使っています。最初にも述べましたが、一般的な債券では、まず市場価格ありきで、そこから内部収益率(IRR)を使って利回りを求めるので、特にイールドカーブを必要としません。しかし、デリバティブズが組み込まれた仕組み債などの価格評価には、それ専用のPricing Engineとイールドカーブが必要になります。
ここで構築されるイールドカーブは、ベンチマーク債券の価格から構築されるものと、LIBOR-Swapカーブの2種類です。前者は、Discounting Curveとして債券キャッシュフローの現在価値(すなわち債券価格)計算に使われ、後者はForacasting Curveとして、変動利付債のクーポン額の予想に使われています。
債券は、ゼロクーポン債、固定金利債、および変動利付債の3種類の商品オブジェクトを構築しています。
価格エンジンは、債券イールドカーブを引数として、DiscountingBondEngineクラスのインスタンスを生成し、それを3種類の商品オブジェクトに設定しています。
後は、価格エンジンを走らせるだけです。前の2つの例(EquityOptionとSwap)と同じように、Instrument オブジェクトのメソッドである NPV() を呼び出せば、価格計算が出来ます。債券の商品オブジェクトでは、NPV()以外に、cleanPrice()、dirtyPrice()、accruedAmount()メソッドも用意されており、それぞれ”経過利息を含まない価格”、”経過利息を含む価格”、”経過利息”を計算し出力します。いずれも、債券の額面に対する%表示で返されます。
また、最後の方で計算している yield()メソッドは、市場価格をもとに、内部収益率を債券のクーポン支払い回数に対応した複利表示返します。
< ステップ毎のコード解析 >
では、プログラムコードを手前から解説していきます。
① 例外処理
これまでと同じく、main( )関数内をtry{…} で囲んでおり、例外処理が発生した場合の対応をしています。
② boost::timerのセット
これまでの例と同じです。上のConsole画面出力にある通り、今回のテストプログラムの計算時間は2秒でした。イールドカーブを2種類構築しているので、計算時間の大半はこの部分と推察します。
③ 日付とカレンダーの設定
71行目で、カレンダーを TARGET に設定しています。TARGET は既に説明した通り、ECB (欧州中銀) の資金グロス決済システムの事で、このシステムがオープンしている日を営業日とするカレンダーです。
また、73行目で、決済日として2008年9月18日を指定し、さらに fixingDays=3、settlementDays=3という変数を設定しています。fixingDays は変動金利の決定日から対象金利期間のスタート日までの日数です。settlementDays は、債券の取引日から決済日までの日数です。ここで指定している数字は、実際の取引慣行と異なっていますが、あくまでテストなので気にしないでいいでしょう。
債券の価格計算は、実務慣行では通常、決済日を規準にしています。従って本日と settlementDays の情報から、価格計算基準日を求めます。デリバティブズの価格計算の基準日が、通常"本日"なので、それと異なる日になる事に注意が必要です。
④ イールドカーブの構築
90行目から、イールドカーブの構築です。先ほど説明した通り、債券Cash Flowを現在価値に割引く為の、Discounting Curveと、変動利付債の変動クーポンを推定する為の、Forecasting Curve の2種類のカーブを構築しています。
イールドカーブの構築方法は、既にMulticurveBootstrappingの例で詳しく説明しました。再度簡単に説明すると、まずイールドカーブを構築する部品を生成します。市場データを格納するSimpleQuoteオブジェクトから始まり、それを使ってBootstrapHelperオブジェクトを生成し、さらにその配列を使ってYieldTermStructureオブジェクトを構築します。BootstrapHelper(の派生クラスであるRateHelper)の役割や、市場データの更新に対応するObserverパターンの仕組みについては、MulticurveBootstrappingのセクションで再度確認して下さい。
④-1 Discounting Curve の部品の生成
債券の価格評価に使うイールドカーブは、同質の債券のベンチマーク商品から構築する必要があります。この例では、ベンチマーク商品として、短期ゾーンは割引債を使い、中長期ゾーンはクーポン債を使っています。それぞれ商品性が異なるので、それに合わせたBootstrapHelperクラスが使われています。
まず、105から129行目で、短期ゾーンの商品に合わせた 'BootstrapHelper'オブジェクトを生成しています。まず、市場レートを 'SimpleQuote'に格納し、それを使って'DepositRateHelper'オブジェクトを生成してます。ベンチマーク商品として’割引債’を使っていますが、割引債もインターバンク預金も、償還日(満期日)に一本の Cash Flow が発生するだけなので、期間や日数計算方法を変えるだけで、同じ DepositRateHelper が使えます。
次に、132から196行目で、中長期ゾーンの’クーポン債’に合わせたBootstrapHelperオブジェクトを生成しています。債券のベンチマーク商品の市場データは、通常、利回りでは無く、価格で得られます。従って、BootstrapHelperは、それに対応するものでなければなりません。ここでは、FixedRateBondHelperクラスが使われています。このクラスはBondHelperの派生クラスで、さらにBondHelperは、BootstrapHelperの派生クラスです。
このように、QuantLibでは、ベンチマーク商品のタイプに合わせたBootstrapHelperが用意されています。イールドカーブを、Bootstrapping+Interpolation法で構築する場合、使われるベンチマーク商品に合わせて、適当なクラスを組み合わせればいいだけです。MulticurveBootstrapping の例では、OISRateHelper, DatedOISRateHelper, FutureRateHelper, FraRateHelper, SwapRateHelper, DepositRateHelper が使われました。今回の例で使われた FixedRateBondHelper も含め、QuantLib で用意されているこれらのクラスの継承関係の図を添付します。(QuantLibのReference Manualから抜粋しました。)
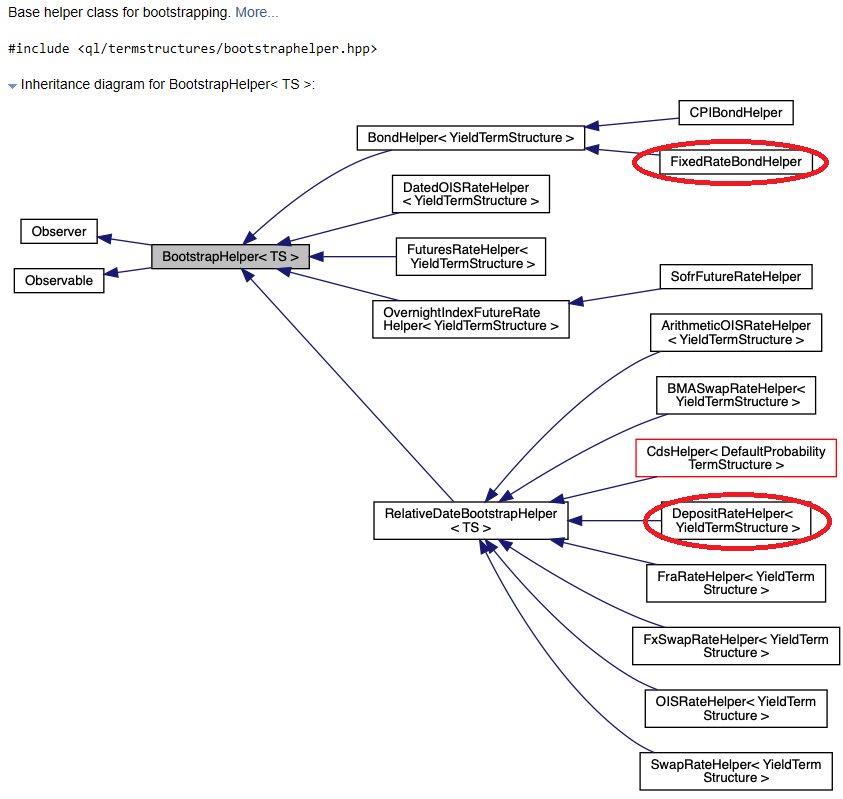
BootstrapHelperクラスは、ベンチマーク商品の価格計算機能を提供しています。従って、その機能に必要な部品を使って組み立てられています。ここでは、FixedRateBondHelperインスタンスを5つ生成していますが、それぞれ市場価格(Quoteオブジェクト)と、対象となる固定金利債の条件(クーポンや償還日など)などを、コンストラクターに取り込んで組み立てています。
BootstrapHelperが揃ったところで、それをひとつに纏め、イールドカーブを構築します。223行目で、bondInstruments という名前の BootstrapHelper の配列を生成しています。226~233行目で、この配列変数に、各 BootstrapHelperインスタンスを代入しています。これで Discounting Curve の部品が揃いました。
④-2 Discounting Curveの構築
235行目で、上記の bondInstruments を使って、'bondDiscountingTermStructure'という名前のイールドカーブを生成しています。このオブジェクトは、PiecewiseYieldCurve<Discount, LogLinear> というテンプレートクラスを使って生成されています。このテンプレートクラスについては、MulticurveBootstrapping の例で既に説明しました。再度簡単に説明すると、テンプレート引数を使って、QuantLibが用意したBootstrapping + Interpolationのアルゴリズムを使って、具体的なイールドカーブインスタンスの構築を、コンストラクターを起動するだけで済ませています。これで、債券Cash Flowの現在価値を計算する為のイールドカーブが完成しました。
④-3 Forcasting Curveの構築
243~381行目までは、変動利付債の将来のクーポンキャッシュフローを予測する為に必要なイールドカーブを構築しています。内容は、前のMulticurveBootstrappingの例で説明したのと同じなので、省略します。
385と387行目で、イールドカーブを保持する為の RelinkableHandleオブジェクトを2つ生成しています。Handle についても、Swap の所で説明しました。即ち、価格エンジンオブジェクトの主要部品であるイールドカーブについて、それが複数ある事を想定し、価格エンジン側で自由に取り換えが出来る様な仕組みを提供しています。
⑤ "Pricing Engine" と "Instruments" オブジェクトの構築
部品が揃ったので、価格エンジンと商品オブジェクトが生成できます。まず 397 行目で、DiscountingBondEngineクラスのインスタンスを生成しています。この価格エンジンは、イールドカーブから Discount Factor を取りだし、それを使って商品のキャッシュフローを現在価値に換算するだけです。コンストラクターは、イールドカーブオブジェクトを取り込んでいます。これで価格エンジンが完成しました。たったこれだけです。
次に商品オブジェクトを生成し、そこに価格エンジンを設定します。この例では、3種類の債券オブジェクトを生成しています。すなわち、ゼロクーポン債、固定金利債、変動利付債です。
⑤-1 ゼロクーポン債の生成
401行目で、ゼロクーポン債を生成しています。ゼロクーポン債は、最もシンプルな Cash Flow を持つ商品なので、部品を事前に作っておく必要がなく、コンストラクターに必要な情報を直接渡して完成です。 さらに、410行目で、先ほど生成した価格エンジンを設定しています。
⑤-2 固定金利債の生成
次に固定金利債を生成しています。固定金利債は、固定金利のクーポンキャッシュフローを持ちます。従って、このオブジェクトを作るには、クーポン支払日の配列から作る必要があります。
そこで、413行目でScheduleオブジェクトを生成しています。この部品は、クーポン支払日の配列を、指定された取引慣行に従って、自動的に生成するオブジェクトです。このオブジェクトを生成するコンストラクターを見て下さい。米国国債の取引慣行に従ってScheduleを生成していますが、その為に引数として次の様な情報を指定しています。
Schedule fixedBondSchedule( Date(15, May, 2007),
Date(15,May,2017),
Period(Semiannual),
UnitedStates(UnitedStates::GovernmentBond),
Unadjusted,
Unadjusted,
DateGeneration::Backward,
false); 引数を個別に見ていきます。
・債券発行日:15,May,2007
・償還日:15,May,2017
・クーポン支払回数:Period(Semiannual) (年2回払い)
・カレンダー:UnitedStates(UnitedStates::GovernmentBond) (米国政府債カレンダー)
・休日の取扱い(クーポン日):Unadjusted (休日を考慮しない)
・休日の取扱い(償還日):Unadjusted (休日を考慮しない)
・クーポン日の設定方法:Backward (償還日を基準に遡りながらクーポン支払日を決める)
・月末の取扱い:false
・First Long/Short Couponの日付:デフォールト設定(Null) (特に指定しない)
・Last Long/Short Couponの日付:デフォールト設定(Null) (特に指定しない)
債券発行日、償還日、クーポン支払回数については、特に注意する点はありません。カレンダーについては、米国政府債用のカレンダーが指定されています。このカレンダーは、FRBの決済システム(FED-Wire)がオープンしている営業日を指定しています。あえて専用のカレンダーがある意味は、米国政府債が取引できる営業日が、必ずしも米国の株式市場の営業日と一致しない為です。
クーポン日と償還日の休日の取扱いは、いずれも’Unadjusted’で指定されています。米国国債のクーポン日や償還日が休日と重なった場合、実際に支払われるのは翌営業日です。しかしその場合でも、遅れた日数分のクーポン額の調整は行われません。
クーポン日の設定方法は Backward で指定されています。これは、償還日を基準に、年2回払いなので、償還日から遡って半年ごとにクーポン日を決めていきます。
月末の取扱いが False となっています。これはクーポン日・償還日が月末の場合、前営業日に戻るのではなく、翌月の最初に営業日になる事を意味します。但し、支払い期間が延びた分に該当するクーポン額の調整は、先ほど述べたように Unadjusted で、何も行われません。
最後の2つの引数については、デフォールト設定を使っているので、Exampleのコード中のコンストラクターでは省略されています。米国国債の期間が、仮に5年2カ月といった端数年の期間であった場合、最初、あるいは最後のクーポン期間だけ6カ月より長かったり短かったりします。そういた場合のクーポン日を指定します。この例は、そういうケースに該当しないのでNull設定になっています。米国債では最近、端数の期間で発行される銘柄を殆ど見ないので、あまり馴染みのない取引慣行かと思います。
以上が、Scheduleオブジェクトを生成する為に必要な情報です。これらの情報は、商品や市場によって様々です。金融商品のオブジェクトを生成するには、コンストラクターでこういった取引慣行を設定する必要があり、どの様なバリエーションがあるか理解していなければなりません。そのバリエーションは多様であり、実務で金融商品のトレーディングやリスク管理を行っている者にとって、ひとつの大きなハードルです。
最後に、418行目で、たった今作った Schedule オブジェクトと、必要な追加情報をコンストラクターに渡して、固定金利債のオブジェクトを生成しています。部品さえ用意されていれば、商品オブジェクトの生成は、このように簡単です。さらに 427行目で、このオブジェクトに価格エンジンを設定しています。
この例では、'Schedule'オブジェクトを、ひとつの部品として、事前に作っておいて、後で、'FixedRateBond'オブジェクトのコンストラクターに渡しています。実は、FixedRateBondクラスのコンストラクターには、別の方法も用意されています。すなわち Schedule オブジェクトを、FixedRateBond とは別に作成するのではなく、必要な情報を FixedRateBond のコンストラクターに渡して、そのコンストラクターの中で作ってしまうものです。そのコンストラクターのコードを"fixedratebond.cpp"ファイルから抜粋したものを下記します。コンストラクターの中で、Scheduleオブジェクトを生成しているのが、分かると思います。Scheduleオブジェクトを生成するのに必要な情報・部品は、FixedRateBondのコンストラクターの引数や、そのコンストラクターの中で生成される変数を使って用意されています。
FixedRateBond::FixedRateBond(Natural settlementDays,
const Calendar& calendar,
Real faceAmount,
const Date& startDate,
const Date& maturityDate,
const Period& tenor,
const std::vector<Rate>& coupons,
const DayCounter& accrualDayCounter,
BusinessDayConvention accrualConvention,
BusinessDayConvention paymentConvention,
Real redemption,
const Date& issueDate,
const Date& stubDate,
DateGeneration::Rule rule,
bool endOfMonth,
const Calendar& paymentCalendar,
const Period& exCouponPeriod,
const Calendar& exCouponCalendar,
const BusinessDayConvention exCouponConvention,
bool exCouponEndOfMonth)
: Bond(settlementDays,
paymentCalendar==Calendar() ? calendar : paymentCalendar, issueDate),
frequency_(tenor.frequency()), dayCounter_(accrualDayCounter) {
maturityDate_ = maturityDate;
Date firstDate, nextToLastDate;
switch (rule) {
case DateGeneration::Backward:
firstDate = Date();
nextToLastDate = stubDate;
break;
// other cases 省略
default:
QL_FAIL("unknown DateGeneration::Rule (" << Integer(rule) << ")");
}
Schedule schedule(startDate, maturityDate_, tenor,
calendar, accrualConvention, accrualConvention,
rule, endOfMonth,
firstDate, nextToLastDate);
cashflows_ = FixedRateLeg(schedule)
.withNotionals(faceAmount)
.withCouponRates(coupons, accrualDayCounter)
.withPaymentCalendar(calendar_)
.withPaymentAdjustment(paymentConvention)
.withExCouponPeriod(exCouponPeriod,
exCouponCalendar,
exCouponConvention,
exCouponEndOfMonth);
// other construction of member variables 省略
}さて、せっかく具体的な金融商品オブジェクトのコンストラクターの中身を示したので、その組み立て作業の中で、Schedule以外にもうひとつ重要な部分を説明したいと思います。すなわち、その金融商品の具体的なキャッシュフローを生成する部分です。基礎編の冒頭で、すべての金融商品はキャッシュフローの集合であると述べました。金融商品を生成する作業の大半は、具体的なキャッシュフローの、'正確な日付' と '金額' を特定する事と言えます。たった今説明した、Scheduleオブジェクトは、その'正確な日付'を特定する為の部品です。一方、以下に説明するCouponオブジェクト(と、その配列であるLegオブジェクト)は、キャッシュフローの'正確な額'を計算する為に必要になります。
上のコードの中で cashflows_ = FixedRateLeg(schedule) の部分と、その下にある .with…( ) の部分をご覧下さい。ここで、キャッシュフローの配列である cashflows_ を生成しています。(デザインパターンに馴染みのある方は、Factoryパターンが使われてるのが、すぐに判ると思います) ここでは見えませんが、背後で個別のCouponインスタンスを生成するプロセスが動いています。
< Couponオブジェクトについて >
ここで、キャッシュフローの基本単位である、Couponクラスについて、少し説明したいと思います。
Couponクラスは、CashFlowクラスから派生しており、CashFlowクラスはEventクラスから、さらにEventクラスはObservableクラスから派生しています。すなわち
Observable ← Event ← CashFlow ← Coupon ← (具体的クラス)
という階層になっています。Observableについては、既に説明しました。Eventクラスですが、特定の日付に発生する経済事象を抽象化したクラスです。経済事象とは、Cash Flowの発生や、オプション期日の到来、オプションの行使、などが想定されています。従って、このクラスのメインのインターフェースは、そういった事象が発生したか否かを返すhasOccured( )と、その発生日付を示すdate( )になります。そして、そこから派生するCashFlowクラスは、読んで字のごとく、Cash Flowの発生事象を抽象化したクラスです。この階層でも、まだ抽象クラスです。Cash Flowの構成要素は、“日付”と“金額”になりますが、この階層では、いずれの情報もメンバー変数として持っていません。しかし、純粋仮想関数としてamount( )メソッドが宣言されており、その内容は派生クラスで実装する必要があります。このメソッドの機能は、名前から明白で、Cash Flowの金額を返します。
そして“Coupon”クラスがそこから派生しています。実は、この階層でもまだ抽象クラスで、このクラスのインスタンスを作る事はできません。このクラスは、債券のクーポン属性をオブジェクトモデル化したクラスです。債券のクーポンに共通する属性として思い浮かぶものを挙げてみると、“クーポンレート”、“クーポン計算期間”、“クーポン支払日”、“クーポン日が休日の取扱い”、“クーポン金額”、“経過利息の計算”、などがあります。従って、このクラスは、こういった属性の情報にアクセスできるインターフェースと、メンバー変数を持ちます。メンバー変数では、クーポン支払日、クーポン計算期間、クーポンレート参照期間、みなし元本額などの情報を持ちます。しかし、肝心の“クーポンレート”を保持するメンバー変数がありません。またインターフェースの一部も純粋仮想関数として宣言されているだけであり、このままでは使えません。このクラスから、さらにクーポンのタイプを細かく類型化し、具体的な派生クラスを作っていきます。
“FixedRateCoupon”クラスは、Couponクラスから派生した具体的クラスで、ここで初めてインスタンスを生成する事が出来ます。固定金利クーポンの属性や計算機能をカプセル化したクラスです。メンバー変数として、InterestRateクラスの変数 rate_ を持ちます。この変数の意味は名前から明白です。この値を使って、Couponクラスで宣言された様々なインターフェースの実装が行えます。InterestRateクラスは、金利に関する meta-data を保持するクラスです。金利は、例えば年率2.5%と表示されていても、複利の回数や、日数計算方法の違いによって、実際に支払われる金額が異なってきます。そういった情報も含めて、金利の情報をカプセル化したクラスが InterestRateクラスになります。
このFixedRateCouponクラスは、一本の Coupon情報のみを取り扱います。通常、債券のクーポンは複数存在するので、これの配列を作る必要があります。それが、一般的なキャッシュフローの配列を取り扱う“Leg”クラスになります。
Legクラスは、CashFlowクラスの配列ですが、typedefを使って下記のように定義されています。
typedef std::vector<boost::shared_ptr<CashFlow>> Leg;すなわちCashFlowオブジェクトへのスマートポインターを Template 引数として取る配列変数です。Template引数として CashFlowクラスの任意の派生クラスを取る事が出来きます。
債券クーポンの'Leg'を作るには、クーポン毎に、クーポン支払日、クーポン計算期間、その期間に適用となる元本額(減債条項付きの債券の場合、元本が逓減していきます)などの情報を設定する必要があります。その作業をする為に作られたクラスがあり、“FixedRateLeg”がそれです。このクラスはLegクラスの派生クラスではありません。Legを生成する為のHelperクラスになります。クーポン毎の支払日やクーポン計算期間など、日付に関する情報は、引数として受け取ったScheduleインスタンスから取り寄せ Leg を組み立てます。ここではFactory パターンが使われている様子が判ります。 Cash Flowの Leg が出来れば、価格エンジンの役割は、それを現在価値に割引くだけです。
部品さえ揃えば、FixedRateBondオブジェクトを構築するのは簡単です。それらの部品をコンストラクターに渡せば終わりです。しかし、そのコンストラクターが裏で行っている作業は、Scheduleオブジェクトの生成や、クーポンキャッシュフローの生成など、膨大です。しかし、それらはすべてQuantLibがデフォールトで用意しています。ユーザーは、必要な部品を集めてくるだけです。
⑤-3 変動金利債の生成
テストコードから大分それたので、元に戻します。
431 から 460 行目で変動金利債オブジェクトを生成しています。一般的な変動金利債は、クーポンレートが LIBOR 等の金利インデックスに従って定期的に見直されます。また、クーポンレートの決定方法に様々なバリエーションがあったり、CAP や FLOOR などのオプションが付随したりして、固定金利債よりはるかに複雑です。従って、必要な部品も、固定金利債よりはるかに多くなります。
その中で、最も重要な部品は変動金利インデックスのオブジェクトです。この例ではLIBORインデックスのオブジェクトを生成しています。また、先ほどの固定金利債と同様、クーポン日の配列(Scheduleオブジェクト)も必要となります。
さらに、クーポンにデリバティブズのリスクが組み込まれる場合は、クーポン毎に、価格エンジンに相当する部品が必要になります。この例でも、CouponPricerと呼ばれるクラスを使って、そのオブジェクトを生成しています。Exampleコードを見ながら、これらの部品が作られる所から見てみます。
まず 432 から 435 行目で、US$ の3か月LIBORインデックスのオブジェクトを生成しています。変動金利インデックスは、将来の変動金利キャッシュフロー額の予想に使われるので、Forecasting Curveとなるイールドカーブが必要です。432行目でまず YieldTermStructureオブジェクトへの Handle(ポインターへのポインター)が生成されています。この時点では具体的なイールドカーブが指定されていませんが、後でこの Handleを接続ソケットのように使って具体的なイールドカーブをはめ込みます。そして、このHandleを部品として、USDLiborインデックスのオブジェクトを生成しています。さらに、435行目は、既にFixingが終わって確定している、変動金利クーポンを設定しています。
< 金利インデックスについて >
Exampleから少し離れて、QuantLibで定義されている“金利インデックス”オブジェクトについて説明します。このインデックスの中で、最も一般的なのは、LIBORインデックスです。433行目で生成された"USDLibor"クラスのインスタンスがそれに該当します。このクラスは、次の順序で派生してきたクラスです。(左にいくほど抽象化が進んだベースクラスになります)
Observable ← Index ← InterestRateIndex ← IborIndex ← Libor ← USDLibor
↓
Observer
このクラス階層の内、Observer と Observable については、説明済みです。それを除くと、基本となるベースクラスは、"Index"クラスになります。Index は、ここでは“金融指標”と訳すのが最も適当でしょう。金融指標とは、金利の他にも、株式、為替、債券、クレジットなどさまざまな金融商品のグループ(ポートフォリオとかバスケットと呼んでもいいでしょう)の'価格'や'金利水準'を代表する数値です。さらに、インフレーションスワップやインフレーションリンク債などは、各国のインフレ率を金融指標として使うので、こういった指標も取り扱えるクラスです。このベースクラスは、抽象クラスで、ここで宣言されているメソッドは、ほとんどが純粋仮想関数です。また、それらのメソッドは、すべての Index に共通するようなインターフェースを提供しています。QuantLibの開発者が考えた共通するインターフェースとは、基本的には、日付に対応するインデックスの値の設定と、設定された値へのアクセス方法になります。
このベースクラスから、"金利"に関するインデックスを取り扱うクラスとして、"InterestRateIndex"クラスが派生しています。金利に関するインデックスは、LIBORのようなロンドン市場におけるインターバンク金利以外にも、コール金利、Federal Fund金利、Swap金利、など様々な金利関連商品のインデックスがあります。InterestRateIndex は、それらすべてをカバーするベースクラスになります。このクラスが提供しているインターフェースや、格納しているメンバー変数は、これらの金利インデックスすべてに共通するものです。インターフェースは、主にインデックスの決定(Fixing)に必要な情報へのアクセスを提供しています。メンバー変数は、インデックスの名前や期間、Fixingに必要な日付に関する情報、カレンダーなどです。但し、もともと開発当初は、LIBORを念頭にデザインしていた為、開発者のひとり(Luigi Ballabio)は、若干汎用性に欠ける点がある、と述べています。特に、’インデックス間のスプレッド’のような情報、例えばCMSスプレッドなどは、このクラスで取り扱えません。
さらに、このクラスからIborIndexクラスが派生しています。Iborは、Inter-Bank Offer Rateの略で、銀行間の資金市場(Inter-Bank Money Markets)における、資金の出し手が呈示する金利(Offer Rate、すなわち貸出金利)のことです。インターバンク市場では、Offer Rateに対しBid Rate、すなわち資金の受け手が呈示する預金金利もありますが、大半のインターバンク市場の金利指標は、Offer-Rate(貸出金利)の方を使っています。LIBOR以外にも、通貨Euroのインターバンク市場の金利であるEURIBOR、東京市場のTIBOR(Tokyo Inter-Bank Offer Rate)、などがあり、これらすべてをカバーするベースクラスです。
LIBORクラスは、そこから派生しています。ロンドンのインターバンク資金市場における取引慣行などをカプセル化したクラスになります。そこから、通貨ごとのクラスが派生し、それが最終的に具体的なクラスになり、そのインスタンスを生成して使うことができます。このExampleでも、最終的にUSDLiborクラスのインスタンスを生成しています。ここでは、US$の3か月Liborクラスを生成しています。そのコンストラクターは、LIBOR・Swapイールドカーブを引数として取っており、このカーブを使って、現在あるいは将来の、特定の時点における3か月Libor金利をFixingあるいは推定します。
Indexクラスは、あくまでインデックスの‘Fixingに必要な情報’や、‘Fixingの方法’をカプセル化したオブジェクトモデルで、Fixing後のデータを保持するクラスでは無い点に注意して下さい。このクラス階層の、どの段階にもFixingされた指標の値を保持するメンバー変数はありません。実は、Fixing 後のデータは、"IndexManager"と呼ばれるオブジェクトに、すべてまとめて保管されています。このExampleのコードには出てこないので、その説明は省略します。
Indexクラス全体の説明は、Luigi Ballabioの“Implementing QuantLib”の中の“Odds and Ends”の中で、解説している部分があるので、そちらを参考にして下さい。IndexManagerについても、説明があります。
再びコードに戻ります。437行目でクーポンキャッシュフローのScheduleオブジェクトを生成しています。そのコンストラクターの引数は次の様になっています。
Schedule floatingBondSchedule(
Date(21, October, 2005),
Date(21, October, 2010),
Period(Quarterly),
UnitedStates(UnitedStates::NYSE),
Unadjusted,
Unadjusted,
DateGeneration::Backward,
true);各引数の意味は、既に説明した通りです。実際に使われている引数(すなわち部品)は固定金利債のScheduleオブジェクトと、微妙に異なります。この設定内容についても、具体的な債券で使われている取引慣行に基づいて設定する必要があります。(クーポン日と償還日の休日の取扱いが、いずれもUnadjustedになっています。一般的な変動金利債では、Modified Followingが多いですが、テストコードなので気にしないでいきます)
442から461行目で、以上の部品と、他に必要な情報をコンストラクターに渡し、FloatingRateBondオブジェクトを生成しています。コンストラクターにどのような引数が渡されているか、見てみましょう。
・決済期間:settlementDays (取引日から決済日までの期間。77行目で3日に設定)
・額面:faceAmount (債券の額面。393行目で100に設定)
・クーポン日のスケジュール:floatingBondSchedule (先ほど生成した主要部品)
・金利インデックス:libor3m (先ほど生成した3カ月物USD LIBORインデックス)
・日数計算方法:Actual360() (USD-LIBORの日数計算方法 実日数/360日)
・休日の取扱い:ModifiedFollowing (クーポン日が休日の場合、次の営業日にする。但し、休日が月末の場合は、次営業日が翌月になるので、前営業日に戻る。)
・金利決定期間:2 (金利のFixingはクーポン期間開始の2営業日前)
・ギアリングの配列:(1, 1.0)(Reverse Floaterクーポンにおける変動金利にかける倍率。配列にしているのは、クーポン毎に設定する為。ここでは一般の変動金利債なので、配列は1で倍率は1.0に設定。要は何もしない。)
・スプレッド:(1, 0.001)(変動金利のスプレッド。配列にしているのはクーポン毎に設定できるようにする為。ここでは一律0.1%)
・CAP:Null() (変動金利の上限金利。CAP付き変動金利債の場合に使う。)
・FLOOR:Null() (変動金利の下限金利。FLOOR[月の変動金利債の場合に使う)
・金利Fixingの後決め:true (変動金利を金利期間の最後に決める。ここではtrueだが、あまり一般的では無い。)
・償還価格:100 (額面100%で償還)
非常に多くの情報が、コンストラクターに渡されているのが判ります。これまで、様々な変動金利債のバリエーションが開発され、発行されてきた歴史を反映しています。こういったバリエーションは、実は1980年代に大半が開発されていましたが、最近はあまり見かけなくなりました。従って、金融実務に携わってあまり時間が経ってない人にとっては、各設定情報の意味が判りにくいかもしれません。しかし、これらの情報は、大半のデリバティブズシステムでも使われており、実務で慣れていくしかありません。
< Coupon Pricerについて >
CouponPricerについて、少し説明したいと思います。債券オブジェクトに設定される価格エンジンは通常、Discounting Curve を使って債券のクーポンと償還額Cash Flowの現在価値合計を計算します。この値が債券の'NPV'すなわち(経過利息込みの)債券価格です。この場合、債券キャッシュフローを確定的なものとしてとらえ、その現在価値を計算しているだけです。しかし Cap や Floor が付いたクーポンは、一種の金利オプションであり、その価格計算には、何等かのオプション価格計算のエンジンが必要になります。あるいは、金利インデックスが、CMS(Constant Maturity Swap) の場合も、何等かのオプション価格エンジンが必要になります。それが、CouponPricer になります。
CouponPricerは一種の簡易版価格エンジンで、それが個別の'FloatingRateCoupon'オブジェクト毎に設定されます。 QuantLibのライブラリーを見てみると、通常の Cap/Floor付きクーポンで使われる、BlackIborCouponPricer や、CMSリンクのクーポンで使われる CmsCouponPricer などが見当たります。変動利付債のクーポンの態様は千差万別で、それぞれの種類についてCouponPricerが必要になるでしょう。このLibraryを拡張して使うUserは、価格計算をしようとしている変動利付債の種類ごとに、CouponPricerが既に用意されているかどうか、チェックする必要があります。もし用意されていないのであれば、自分で開発する必要があるでしょう。
このExampleでは、466行目に、BlackIborCouponPricerクラスのインスタンスを生成しています。オプションの価格を計算するには、パラメータとしてVolatilityの情報が不可欠であり、469から478行目で、そのVolatilityのTerm Structureオブジェクトを生成しています。これを、BlackIborCouponPricerにセットしてCouponPricerが生成されました。481行目で、そのCouponPricerを、すでに作成済の変動利付債の商品オブジェクトに設定しています。但し、ここでは、Volatilityの値が 0 に設定されており、オプションの価格計算上、意味の無い値になっています。CAP も FLOOR も付いていないので、そもそもオプション価値を計算する必要がなかったのです。
459行目にある、FloatingRateBondコンストラクターのfixing in arears(金利Fixing後決め設定)引数がtrueになっており、厳密にはConvexity Adjustmentが必要です。従って、その為に何等かのCouponPricerが必要ですが、ここではその計算は行っていません。BlackIborCouponPricerを設定しているものの、そのPricerには、Convexity Adjustmentを計算する機能は備わっていないようです。また、QuantLibのライブラリーを見ても、それ用のCouponPricerが見つかりませんでした。現在のような低金利環境で、イールドカーブの勾配も緩やかな場合、Convexity Adjustmentの額も微小なので、特に気にする必要は無いと思います。
以上で、(i) 価格エンジンの部品から、価格エンジンオブジェクトの生成、(ii) 3種類の商品オブジェクトの生成、(iii) 価格エンジンを商品オブジェクトに設定、そして(iv) 変動利付債用にCouponPricerを生成し設定する作業、が終わりました。後は、NPV( )を走らせて、価格計算をするだけです。
⑥ 計算の実行
494行目以降は、3種類の債券について、価格や利回りの計算を実行し、それを Console画面に出力しています。債券オブジェクトが持つ、NPV()、cleanPrice()、dirtyPrice()、accruedAmount()、previousCouponRate、nextCouponRate() 、yield()といったインターフェースを使って、価格計算アルゴリズムを呼び出し、その計算結果を出力しています。インターフェースは債券オブジェクトのものですが、実際の計算アルゴリズムは価格エンジンやCouponPricerが担っています。
これまでのステップを見る限り、価格計算までのプロセスは相当複雑な操作です。債券トレーディングの実務で使われている、価格から最終利回りを計算する方法や、最終利回りから価格を計算する方法は、もっと簡単ではないかと思われる方もいるでしょう。ここで走っているアルゴリズムは、イールドカーブの期間構造(Term Structure)を使った現在価値計算方法であり、Swapなどのデリバティブズの現在価値計算と同じ方法を使っています。従って、イールドカーブの構築が必要になり、それに相当の手間がかかっています。また変動利付債のCouponPricerは、一種のオプション価格エンジンであり、通常の債券価格、債券利回り計算のアルゴリズムとは相当異なります。
シンプルな固定金利債や、変動利付債の利回りや価格計算は、もっと簡単にアルゴリズムが構築可能です。市場慣行で使われる利回りは、内部収益率(Internal Rate of Return)の考え方をベースにしています。そこでは、すべてのキャッシュフローについて金利の期間構造を勘案せず、同じ利回りになる前提で計算されています。すなわち現在から債券の満期日まで、同じレートで再投資・再運用できるとう仮定のもとで計算される利回りです。561~568行目の計算は、その方法で行ったものです。メソッド名cleanPrice() とyield()を異なる引数でOverloadしたメソッドで、背後にあるアルゴリズムは、BondFunctionsクラスが提供する関数群を使っています。BondFunctionsクラスは、さらにCashFlowsクラスの関数群を呼び出しており、アルゴリズムの実体は、CashFlowsクラスの中で定義されています。
以上で、このExampleの説明は終わりです。
<ライセンス表示>
QuantLibのソースコードを使う場合は、ライセンス表示とDisclaimerの表示が義務付けられているので、添付します。 ライセンス