2. "Implementing QuantLib"の和訳
Chapter VIII The Finite-Difference Framework (有限差分法のフレームワーク)
8.2 The New Framework (新しいフレームワーク)
8.2.2 Operators : 差分演算子
FdmLinearOpクラスのインターフェースを下記 Listing 8.20 に示します。このクラスの中心的な機能は apply( )メソッドで、引数として与えられた配列に対し、Operator(差分演算子)を作用させ、その結果を返す事です。古いフレームワークの中の applyTo( )メソッドが同様の機能を持っていた事を覚えておられるでしょう。(注:もうひとつの機能であるtoMatrix( )メソッドの説明は飛ばします。このメソッドはOperator(演算子) をMatrixとして返すだけで、単なるインスペクター関数の一種です。)
Listing 8.20:FdmLinearOpクラスおよびそのHelperクラスのインターフェース
class FdmLinearOp {
public:
typedef Array array_type;
virtual ~FdmLinearOp() { }
virtual Disposable<array_type> apply(
const array_type& r) const = 0;
virtual Disposable<SparseMatrix> toMatrix() const = 0;
};
class FdmLinearOpIterator {
public:
explicit FdmLinearOpIterator(const std::vector<Size>& dim);
explicit FdmLinearOpIterator(Size index = 0);
FdmLinearOpIterator(const std::vector<Size>& dim,
const std::vector<Size>& coordinates,
Size index)
void operator++();
bool operator!=(const FdmLinearOpIterator&);
};
class FdmLinearOpLayout {
public:
FdmLinearOpLayout(const std::vector<Size>& dim);
FdmLinearOpIterator begin() const;
FdmLinearOpIterator end() const;
Size index(const std::vector<Size>& coordinates) const;
Size neighbourhood(const FdmLinearOpIterator& iterator,
Size i, Integer offset) const;
Size neighbourhood(const FdmLinearOpIterator& iterator,
Size i1, Integer offset1,
Size i2, Integer offset2) const;
}; さて、読者の方はこのコードを見て、インターフェースで使われている array_type は typedef を使って1次元の配列 Array型を使って定義されている事に気づかれたでしょう。私が多次元の Operator(差分演算子)についても対応できると述べた事と矛盾してませんか? 実は、このフレームワークでは、多次元の配列の要素を平らに並べて1次元の配列に変換し、お互いの要素を一対一で対応付けています。
例として、3次元の配列 \(a_{i,j,k}\ (0 \leq i \lt M,\ 0 \leq j \lt N,\ 0 \leq k \lt P) \) があるとします。この3次元配列のすべての要素を、単純に辞書の順序で並べます。最初の要素 \(a_{0,0,0}\) からスタートし、\(a_{1,0,0},\ …\ a_{M-1,0,0}\) と並べていきます。次に2番目の sub-index を1つ進め\(a_{0,1,0}\) から再びスタートし \(a_{1,1,0},\ …\ a_{M-1,1,0}\) のように並べていきます。その次の要素は \(a_{0,2,0}\) となり、同じ事を繰り返し \(a_{M-1,N-1,0}\) に至ります。ここからさらに、\(a_{0,0,1}\) に進みます。もう要領は分かったと思います。同じ事を繰り返し、\(a_{M-1,N-1,1}\) まで行き、さらに \(a_{0,0,2}\) からスタートし、最終的に \(a_{M-1,N-1,P-1}\) で終わります。
上記 Listing 8.20に示している FdmLinearOpIteratorクラス と FdmLinearOpLayoutクラスは、協働してこのロジックをサポートしています。両者ともクラス名を FdmLinearOpクラスにちなんでつけられていますが、実際には Operatorが作用する対象である Arrays(配列)の操作を行っています。
FdmLinearOpIteratorのインスタンスは、多次元配列のインデクスを示すtuple (訳注:ここでは座標を意味し、std::tupleの意味では無い。) と、それらを一本にまとめた配列のインデックスとの関係を管理します。その為には、各次元の配列のサイズ(上記例ではM、N、Pが該当)を保持する必要があります。
呼び出すコンストラクターによって、そういった情報のすべてを、あるいは一部を明示的に引数として渡す事ができます。各次元の配列のサイズだけを引数として取るコンストラクターは (訳注:上記 Listing中の、最初のコンストラクターが該当)、その配列のサイズをメンバー変数に保持し、同時に一本にまとめた配列のインデックス(index_)と座標(coordinates_[ ]) の各次元のインデックスをすべて、暗黙的に 0 で初期化します。すなわち、返し値として配列の最初の要素を示す Iteratorを返します。1個のインデックスのみを引数でとるコンストラクターは、何等かの sentinel値 (訳注:配列の終わりを示す値)を生成しますが、その値はインクリメントできません。なぜなら、この段階では配列のサイズが判っていないからです。しかしそのコンストラクターに一本化された配列のサイズが明示的に渡された場合は、配列の終点を示すIteratorが返され、それをfor loopの終了点として使えます (次の Listingは、そういった使用例です)。
std::vector<Size> dims(...); // { M, N, P }
FdmLinearOpIterator begin(dims);
FdmLinearOpIterator end(M*N*P);
for (FdmLinearOpIterator i=begin; i!=end; ++i)
... // do something 最後のコンストラクターは、各次元の配列サイズ(dim)と、各次元のインデックスのcoordinates (訳注: いわゆる多次元の座標) を引数としてとるので、配列の任意の場所を示す Iteratorを生成する事ができます。おそらく計算パフォーマンスの理由からと思われますが、パラメータが整合的かどうかのチェックは、この情報を呼び出す側に任されています。チェックとは、各次元のインデックスの集合(座標)が一本に並べられた配列のインデックスと対応しているかどうか確認する事です。
FdmLinearOpIteratorインスタンスの役割は、C++言語における iteratorと厳密には同じではありません。なぜならこのクラスは iteratorに要求されるインターフェースをすべて備えていないからです。特に、それが指し示すポイントの値を返す dereference演算子がありません。このクラスで実装している (オーバーロードしている)算術演算子は、operator++()で、これはIteratorをひとつ進める動作をし、operator!=( )は、2つのIteratorを比較します。 (注:operator!=() のみを提供しoperator==()は用意していませんが、for loopの中で i != end というチェック文で使えれば十分だからです。でも省略し過ぎかもしれません。)
この2つのメソッドの実装内容を下記 Listing 8.21に示します。この Listingには載っていない他のインターフェースも簡単に説明すると、この Iteratorは、座標を返す coordinates( )インスペクター関数を宣言しており、また同様のインスペクターである index( )メソッドは座標に対応する一本に並べた配列上のインデックスを返します。
Listing 8.21 : FdmLinearOpIteratorクラスの実装内容(一部)
void FdmLinearOpIterator::operator++() {
++index_;
for (Size i=0; i < dim_.size(); ++i) {
if (++coordinates_[i] == dim_[i])
coordinates_[i] = 0;
else
break;
}
}
bool FdmLinearOpIterator::operator!=(
const FdmLinearOpIterator& iterator) {
return index_ != iterator.index_;
} インクリメント演算子 ++ は文字通り、前のページで説明した配列インデックスの操作 (インデックスをひとつ進める操作) を実装しています。まず、座標の最初の次元の配列インデックスをインクリメント (訳注:コード中の ++coordinates_[i] の部分)し、もしそれによって最初の次元の要素数に到達すれば、その次元のインデックスを 0 に再設定し次の次元のインデックスのインクリメント操作に移ります。そうでなければ、ループから出ます。従って、例えば今3次元のインデックスの値が \((M-1,N-1,2)\) の時に (訳注:第1次元と第2次元のインデックスの値がそれぞれの配列要素数の上限に達している時に)、++ 演算子を呼び出すと、①まず第1次元のインデックスをひとつ増やして \((M,N-1,2)\) となりますが ②(第1次元のインデックスが範囲を越えてしまうので) 第1次元を 0 にリセットし ③第2次元のインデックスをひとつ増やして \((0,N,2)\) とし、さらに ④(第2次元のインデックスも範囲を越えてしまうので) 第2次元のインデックスも 0 にリセットし、⑤第3次元のインデックスをひとつ増やして、最終的にcoordinates_は、\((0,0,3)\) となります。そこで ⑥(3は第3次元の要素数内なので)for loopから出ます。いずれの場合でも、一本化された配列のインデックスも ひとつ増やされており (訳注:コード中の最初の方にある ++index_ の操作)、3次元のインデックスと同期がとれるようになっています。
最後に、operator!= は2つの Iteratorが指し示すインデックスが、一本化した配列の中で同じインデックスを指し示しているかどうかチェックします (ここまでくると“一本化した配列”については、もっと短い名前をつけるべきかもしれません)。これは、Iteratorsに、たとえ、座標のインデックス情報を持っておらず(訳注:座標を格納する配列coordinates_がNullの場合)、それをインクリメントできなかったとしても、sentinel値(配列のサイズの見張り役)の機能を与えています。
FdmLinearOpLayoutクラスは、与えられた配列のレイアウト (すなわち状態変数の次元の集合)をもとに、Iteratorsインスタンスと協働して、いくつかの機能を提供しています (このクラスのインターフェースは上記 Listing 8.20に示されていますが、下記 Listing 8.21にその実装内容の一部を示します)。
Listing 8.21 : FdmLinearOpLayoutクラスの実装内容(一部)
FdmLinearOpLayout::FdmLinearOpLayout(const std::vector<Size>& dim)
: dim_(dim), spacing_(dim.size()) {
spacing_[0] = 1;
std::partial_sum(dim.begin(), dim.end()-1,
spacing_.begin()+1, std::multiplies<Size>());
size_ = spacing_.back()*dim.back();
}
FdmLinearOpIterator FdmLinearOpLayout::begin() const {
return FdmLinearOpIterator(dim_);
}
FdmLinearOpIterator FdmLinearOpLayout::end() const {
return FdmLinearOpIterator(size_);
}
Size FdmLinearOpLayout::index(const std::vector<Size>& coordinates) const {
return std::inner_product(coordinates.begin(),
coordinates.end(),
spacing_.begin(), Size(0));
} このクラスが提供している計算内容の殆どは、各次元の配列要素間の spacing (多次元の配列を一本の配列に並び替えた時の、要素間の間隔)に基づいて行われます。前に使ったのと同じ例を使って説明します。3次元の配列で要素数が \((M,N,P)\) の場合を考えてください。そこから2つの要素(の座標) \((i,j,k)\ と\ (i+1,j,k)\) を取りだしたとします。この2つの要素は、一本化した配列の中では隣同士の場所にあります (先ほどの例で3次元の配列を一本に並べる際、第1次元のインデックスから順番に番号づけしていった事を思い出して下さい)。 仮に、2つの要素が \((i,j,k)\ と\ (i,j+1,k)\) であった場合、一本化した配列の中では、この2つの要素は第1次元の要素数とちょうど同じだけ離れています。この2つの要素間を順番に追っていくと、まず第1次元のインデックスを \((i+1,j,k)\ (i+2,j,k)\) と進んで行き、 \( (M-1,j,k)\) まで到達したところで \((0,j+1,k)\) に行き、そこからさらに \((1,j+1,k) ,\ (2,j+1,k)\) と進んでゆき、最後に \((i,j+1,k)\) でようやく到達します。少し考えれば、この2つの要素間の spacing は M になる事がわかるでしょう。同じように考えれば、第3次元の2つの要素 \((i,j,k)\ と\ (i,j,k+1)\) の間の spacingは M × N になる事もわかるでしょう。
FdmLinearOpLayoutクラスのコンストラクターは、各次元の要素数の配列 \((n_1,n_2,\ …\ n_N)\) を取り、一本化した配列における spacings の配列、すなわち \((1, n_1,\ n_1 × n_2,\ …\ ,\Pi_{i=1}^{N-1}n_i)\) と、その配列の全要素数 \(\Pi_{i=1}^{N}n_i\) を計算します。計算は STL(Standard Template Library)を使っていますが、実際に計算式をコード化してもそれ程難しくなかったでしょう。
配列のサイズと spacings が計算されたので、これを使って、Iteratorと協働しながら、いくつかのメソッドを実装できます。begin( ) と end( )メソッドは、それぞれ対応する Iteratorを返してくれるので、一旦 Layoutインスタンスを得てしまえばもはや sentinels や Iteratorのコンストラクターを気にする必要がなく、つぎのような for loop の構文を書く事ができます。
std::vector<Size> dims(...);
FdmLinearOpLayout l(dims);
for (FdmLinearOpIterator i=l.begin(); i!=l.end(); ++i)
... // do something また index( )メソッドは、多次元の配列インデックス (訳注:coordinates(座標)のこと)から、一本化した配列のインデックスへの変換機能を提供しています。neighbourhood( )といった他のメソッド群は、すこし高いレベルでの動作を行います。このメソッドは、まず引数として与えられた Iteratorからそのポジションを読み取り、そこから引数で指定した次元軸の方向へ、指定されたステップ数だけ動かしたポジションのインデックス (すなわちiterator)を返します。このメソッドをオーバーロードしたもので、同様な動作を2つの方向で行うメソッドもありますが、その中味は同じ動作のメソッドを2回続けて呼び出しているだけです。
ここまで来ると、既に説明した FdmMesherクラスのインターフェースの意味が判ってくるでしょう。dplus( )、 dminus( )、 location( )といたメソッドはすべて、最初の引数としてメッシュの中の特定のポイントを示す Iteratorを取り、2番目の引数として多次元メッシュ上の移動方向を取ります。layout( )メソッドは、FdmLinearOpLayoutインスタンスを返し、そのインスタンスを使って Iteratorを生成する事ができます。(注:メッシュの中の各ポイントは、計算しようとしている金融商品の価格が格納されている配列と一対一で対応しています。従って Iteratorは(インデックスと、格納されている値の)いずれかを表示できます。)
ここで、いくつかの Operator(差分演算子)について説明します。古いフレームワークと同様、最も基本的な差分演算子は、ひとつの変数軸に沿った1階と2階の微分を表現するものです。この場合、“基本的”というのは必ずしも“単純な”という事を意味しません。グリッド間隔が等間隔で無い場合における、3点を使った1階微分(差分)を計算する式は
\[ \frac{\partial f}{\partial x }(x_i)\approx \frac{-h_+}{h_- (h_- + h_+)} f(x_{i-1})+\frac{h_+-h_-}{h_+ h_- } f(x_i)+ \frac{h_-}{h_+ (h_-+h_+ ) } f(x_{i+1}) \\ 但し ~~h_-=x_i-x_{i-1} ~~~~ h_+ = x_{i+1}-x_i ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ \]と表現できます。2階微分(差分)の式も、同様に長くなります。(もし興味があれば、この式の導出方法については、下記 Bowen, Smith、2005[1]を参照) さらに、この式では、ある次元軸の i 番目の状態変数を \(x_i\) という記法を使いましたが、もし多次元の配列を使った場合は、式中の状態変数の記法は \(x_{i,j,k-1,l},\ x_{i,j,k,l},\ x_{i,j,k+1,l}\) といった形になるでしょう。
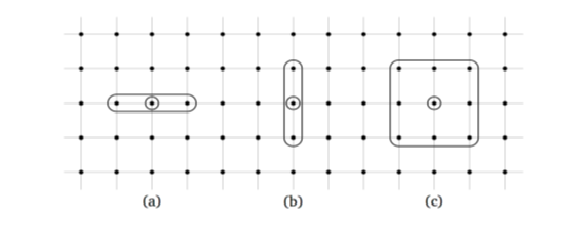
いずれにしても、下記の図の (a) (b) のような2種類の異なる方向に沿った3点のステンシルを使って説明しましょう。
1階と2階の差分演算子はいずれも、TripleBandLinearOpクラスと呼ばれる同じクラスのインスタンスとして表現されます。その実装内容を下記 Listing 8.22に示します。
Listing 8.22 : TripleBandLinearOpクラスの実装内容(一部)
class TripleBandLinearOp : public FdmLinearOp {
public:
TripleBandLinearOp(Size direction, const shared_ptr<FdmMesher>& mesher);
Array apply(const Array& r) const;
Array solve_splitting(const Array& r, Real a, Real b = 1.0) const;
TripleBandLinearOp mult(const Array& u) const;
TripleBandLinearOp multR(const Array& u) const;
TripleBandLinearOp add(const TripleBandLinearOp& m) const;
TripleBandLinearOp add(const Array& u) const;
void axpyb(const Array& a, const TripleBandLinearOp& x,
const TripleBandLinearOp& y, const Array& b);
protected:
TripleBandLinearOp() {}
Size direction_;
shared_array<Size> i0_, i2_;
shared_array<Size> reverseIndex_;
shared_array<Real> lower_, diag_, upper_;
shared_ptr<FdmMesher> mesher_;
};
TripleBandLinearOp::TripleBandLinearOp(
Size direction,
const shared_ptr<FdmMesher>& mesher) : /* ... */ {
shared_ptr<FdmLinearOpLayout> layout = mesher->layout();
vector<Size> newDim(layout->dim());
iter_swap(newDim.begin(), newDim.begin()+direction_);
vector<Size> newSpacing = FdmLinearOpLayout(newDim).spacing();
iter_swap(newSpacing.begin(), newSpacing.begin()+direction_);
for (FdmLinearOpIterator iter = layout->begin();
iter != layout->end(); ++iter) {
const Size i = iter.index();
i0_[i] = layout->neighbourhood(iter, direction, -1);
i2_[i] = layout->neighbourhood(iter, direction, 1);
const vector<Size>& coordinates = iter.coordinates();
const Size newIndex =
inner_product(coordinates.begin(), coordinates.end(),
newSpacing.begin(), Size(0));
reverseIndex_[newIndex] = i;
}
}
Array TripleBandLinearOp::solve_splitting(const Array& r,
Real a, Real b) const {
// ... initializations ...
Size rim1 = reverseIndex_[0];
Real bet=1.0/(a*diag_[rim1]+b);
retVal[reverseIndex_[0]] = r[rim1]*bet;
for (Size j=1; j<=layout->size()-1; j++){
const Size ri = reverseIndex_[j];
tmp[j] = a*upper_[rim1]*bet;
bet=1.0/(b+a*(diag_[ri]-tmp[j]*lower_[ri]));
retVal[ri] = (r[ri]-a*lower_[ri]*retVal[rim1])*bet;
rim1 = ri;
}
for (Size j=layout->size()-2; j>0; --j)
retVal[reverseIndex_[j]] -= tmp[j+1]*retVal[reverseIndex_[j+1]];
retVal[reverseIndex_[0]] -= tmp[1]*retVal[reverseIndex_[1]];
return retVal;
} TripleBandLinearOpクラスの基本的な定義は、TridiagonalOperator(古いフレームワークで説明したのを覚えているでしょうか)のそれに良く似ています。TridiagonalOperatorでは、差分演算子 T を配列 xに作用させると、その計算結果 y は下記の式で表現できます。
\[ y_i=l_i x_{i-1}+d_i x_i+u_i x_{i+1} \]即ち、配列 x の i 番目の要素とその両隣の要素の線形結合で表現されています ( \(l, d, u\) は、三重対角行列の、それぞれ下対角、対角、上対角に該当します)。
TripleBandLinearOpクラスは、この考え方を、多次元に拡大したものです。例えば、4次元の場合 (訳注: x が4次元のベクトルの場合)、その各変数の次元軸を、インデックス \(i, j, k, l\) を使えば、差分演算子が作用する様子は、次のような線形結合で表現できます。
\[ y_{i,j,k,l}=l_k x_{i,j,k-1,l}+d_k x_{i,j,k,l}+u_k x_{i,j,k+1,l} \]この場合でも、あるポイントの要素と、特定の次元軸の方向に沿った (上記式ではk軸の方向の) 両隣の要素の線形結合で表現され、この表現方法がすべての要素について成立しています。 (注:境界にある要素の表現方法については飛ばしますが、存在していない側の隣の要素を無視する事によって、簡単に対応できます。)
入力値と出力値の(多次元ベクトルの)配列を、それぞれ1次元配列に並べ替えると、Operator(差分演算子)は 2次元の行列で表現でき、その行列の要素として値が詰まっているのは、3本の斜め方向のバンド(帯)だけになります。そこからこのクラス名を取っています。前に示した図 (基本的な有限差分スキームで使われるステンシル) をもう一度見てください。ここで水平方向を第1次元、垂直方向を第2次元の軸と仮定し、インデックスの順番が水平方向では左から右へ、垂直方向では上から下へ進んでいくとします。(a)の場合は、中心の点の両隣は、1列に並べ替えた配列上も隣同士であり、Operator(差分演算子)を行列で表現すると三重対角行列になります。(b)の場合は、中心点の上下の点は、1列に並べ替えた配列上では、第1次元の配列の要素数分だけ離れています。従って、Operatorを行列表現すると、null でない要素のバンドは、対角要素のバンド (これも nullではありません)から、相当離れた所にあります。
このクラスのインターフェースには、必須のメソッド apply( )以外にも、いくつかのメソッドが含まれています。solve_splitting( )メソッドは、古いフレームワークの中の solveFor( )メソッドと同じように、Operatorが作用する配列が未知数の場合、連立方程式を解く形で解を導出します。これを使えば、implicit scheme(陰的解法)を使ったコードを書く事ができます (この解法の方が、通常、apply( )メソッドを使ったexplicit scheme(陽的解法)より安定的で、場合によっては計算速度もより速くできます)。mult( )や add( )といった、その他のメソッドは、Operatorに作用する代数演算を定義しており、既存の Operatorインスタンスを線形結合した Operatorを生成する事ができます。(コードの内容をチェックし、どれがどれに該当するかは、読者の方におまかせします。)
コンストラクターは、Operatorを使用可能な状態に持って行く為に、かなりの量の事前計算を行います。まず、Layoutインスタンス中の各点について、指定された次元軸方向の、両隣の点を示す一本化した配列上のインデックスを、配列 i0_ と i2_ に格納します。この作業はlayout->neighbourhood( )の呼び出しを2回行うことによって為されています。この配列を使えば、apply( )メソッドのコアとなる動作を、以下のような簡単なfor loopでコード化できます。
for (Size i=0; i < layout->size(); ++i) {
result[i] = lower_[i]*a[i0_[i]] + diag_[i]*a[i] + upper_[i]*a[i2_[i]];
} ここでは、a[ ]は、Operatorが作用する配列です。このコードが Triple Band Operator(3バンド差分演算子)を使った方程式をコードで表現したものになります。 (注:この apply( )メソッドの中の for loop 計算は、並列処理を行える絶好の候補のように見えるので、実際に、#pragma omp parallel for を加えて、計算スピードアップを図ろうと試みました。しかし、これによって計算速度の向上は見られませんでした。場合によってはパフォーマンスを落としたりしました。もしかしたら、(#pragma文を加えなくとも)コンパイラーが既に並列処理の為の最適化を行っていたのかも知れませんし、何も加えない方が、コンパイラーがよりうまく機能していたのかも知れません。この点については、私自身全くの初心者なので、興味のある読者の方に調べて頂ければと思います。)
コンストラクターは他にも、solve_splitting( )メソッドで使われる配列、reverseIndex_ に値を代入していきます。端的に言えば、このメソッドで使われている、連立方程式を解くアルゴリズムは、古いフレームワークの TridiagonalOperatorで使われているものと同じです。そこでは、配列の値を double sweep (訳注:三重対角行列を使った、高速の連立方程式の解法 ”Solving systems with tridiagonal matrix” Tompson) する手順によって、計算時間をノード数 N の1次のオーダーにできます。その為には、アルゴリズムが、配列を正しい順番で sweepしていく必要があります。正しい順番とは指示された次元の軸に沿ってという事です。上記の図をもう一度見て下さい。通常は一本の配列上での for loop 再帰計算は、配列を水平方向にしか sweepできません。従って、(a)の例では動作しますが、(b)の例では動作しません。
その問題を解決する為、2つめの一本化された配列インデックスを用意しています。例えば、i, j, k, l のインデックスを持つ4次元の配列で、それぞれの要素数が M,N,P,Q の場合を考えてみましょう。k 軸に沿って差分を計算したいとします。一本化された配列上で、Layoutインスタンスが持つ spacing配列には (1, M, M*N, M*N*P) という値が格納されており、座標 (i, j, k, l) の一本化された配列上のインデックス \(I\) は、\(I=i+M*j +M*N*k +M*N*P*l\) となります。そこで、このコンストラクターは、1番目のインデックス (訳注:ここでは i )を差分演算子が計算しようとしているインデックス軸 (訳注:ここでは k ) と入れ替えて、新しい spacing配列を作る事です。この例では (M*N, M, 1, M*N*P) となります。これにより、一本化された配列の新しいインデックス \(\tilde I = M*N*i + M*j + k + M*N*P*l\) が定義され、これを使って配列を sweepして行き、\(\tilde I\) の隣り合う値が k軸 方向の隣りあう要素になります。最後に、各 \(\tilde I\) に対応する \(I\) の値が配列 reverseIndex_ に保存されます。
この操作により、solve_splitting( )メソッドが正しく動作します。2つの for loop の操作によりインデックス \(\tilde I\) の値がすべて必要な順番に並び替えられ、その結果一本化された配列を指定された次元の方向に sweepしていきます。reverseIndex_ 配列は \(\tilde I\) に対応する本来の順番のインデックス I を与え、それを使えば、引数として渡された配列の要素にアクセス出来ます。
新しいフレームワークでは、TripleBandLinearOpクラスに基づいて、与えられた次元方向への、汎用的な1階と2階の差分演算子を定義しています。その概要を下記 Listing 8.23 に示します。見て判る通り、極めて単純です。これらのクラスは、コンストラクターを宣言しているだけで、そのコンストラクターは、lower_ 、diag_、 upper_の配列に正しい値 (例えば、1階の差分方程式の、\(f(x_{i-1}),\ f(x_i),\ f(x_{i+1})\) の各項の係数)を代入しています。
Listing 8.23 : FirstDerivativeOpクラスとSecondDerivativeOpクラスのインターフェース
class FirstDerivativeOp : public TripleBandLinearOp {
public:
FirstDerivativeOp(Size direction, const shared_ptr<FdmMesher>& mesher);
};
class SecondDerivativeOp : public TripleBandLinearOp {
public:
SecondDerivativeOp(Size direction, const shared_ptr<FdmMesher>& mesher);
}; 基本Operatorについてもうひとつ加えると、NinePointLinearOp というクラスも新しいフレームワークの中で定義されています。このクラスは前に説明で使ったステンシルにおける(c)のケースに対応しています。その派生クラスである SecondOrderMixedDerivativeOpクラスは2変数の2階交差偏微分 \( \frac{\partial^2 f}{\partial x_i \partial x_j}\) をモデル化しています。
[1] M. K. Bowen and R. Smith, Derivative formulae and errors for non-uniformly spaced points. In Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences, volume 461, pages 1975–1997. The Royal Society, 2005.
<ライセンス表示>
QuantLibのソースコードを使う場合は、ライセンス表示とDisclaimerの表示が義務付けられているので、添付します。 ライセンス