実務で使える金融工学　上級編

上級編　６．　 Libor Market Model　

6.6  　モンテカルロシミュレーション

6.6.4   分散減少法（Variance Reduction Techniques）

6.6.4.4   層別サンプリング法（Stratified Sampling Methods）

6.6.4.4.1   Stratified Sampling 法の概要

コンピューターのアルゴリズムを使って標準正規乱数を生成する方法については、既に説明しました。そのアルゴリズムで生成された乱数列は、コンピューターゲームなどに使う場合、乱数の発生する順番に規則性があったり、分布が偏ったりしていると問題です。次に出てくる乱数が予想できない、いわゆる“無作為抽出”に見える方法でなければなりません。しかし、乱数を MCS で使う場合、各サンプルの無作為抽出は、それほど重要ではありません。生成された乱数を使って確率変数のサンプル経路をシミュレーションするのですが、大事なのは、すべてのサンプル経路を生成した後に得られる確率変数全体の分布であって、サンプルを生成する順番に規則性（例えば価格の小さい方から生成するなど）があっても、問題ありません。さらに言えば、特定の領域に、サンプルをわざと偏って発生させても、その偏りを後で補正できるなら（いわゆる尤度比が計算できるなら）、元の確率測度での期待値と同じ結果が得られます。 

Stratified Sampling Methods （層別サンプリング法あるいは層別抽出法）は、以上のような考え方に依拠しており、その方法を簡単に説明すると、 

• 確率変数の値域を、互いに重複しない複数の階層に分け
• 各層ごとに、確率測度に比例した（あるいは恣意的な）数のサンプルを発生させ、
• 各層ごとに、条件付き期待値を求め、（サンプル数が恣意的な場合は、尤度比で修正した確率測度での期待値）
• さらに、その期待値の、全領域に渡る確率加重平均を求めれば、
• 全領域での、サンプル平均と一致し、
• 層別化しない場合のサンプル平均と比べて、推定誤差が低減される

というものです。 

確率変数の値域を層別に分割すると言っても、各層の範囲と確率測度が（要は分布関数が）解析的に導出できない場合は、どうやって値域を分割していくのでしょうか？LMM によるフォワード Libor の分布関数は、解析的に求まらないから MCS を使う訳で、将来の Libor の分布を直接層別化する事はできません。さらに言えば、サンプル平均は、このフォワード Libor を対象とするデリバティブズの Payoff 値の平均を求めるのであって、この Payoff 関数の分布を直接層別化するのは、基本的に不可能です。この場合、Libor の拡散過程を駆動するブラウン運動、すなわち標準正規分布する乱数を層別化する事で、結果的に Libor の値域、さらには Payoff 関数の値域を層別化した事になります。 

層別サンプリング法の具体的な方法と、それにより、どの程度推定誤差の低減効果が期待できるかは、後ほど説明しますが、その前に、この方法で、なぜ推定誤差を小さくできるのか、ある程度直観でも理解しやすいように、簡単に説明します。 

コンピューターアルゴリズムで、標準正規乱数を（擬似）無作為に有限個抽出した場合、若干のサンプルの偏りがどうしても発生します。一例として、標準正規分布する確率変数の値域 (−∞,∞) を、標準偏差 0.25 の間隔で等分し（但し両端の層だけは、領域の片側が ±∞）、100 個の標準正規乱数を無作為抽出して各層に配分すると、各層でのサンプル数がどの位になるか、ヒストグラムで見てみます。（下記グラフ） 

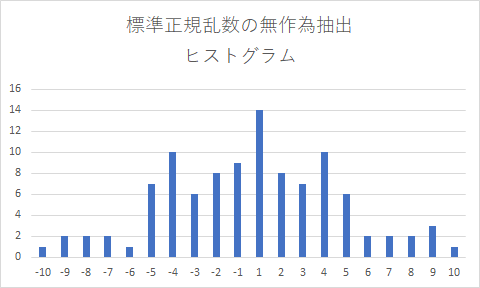
（x 軸の目盛りは、標準偏差 0.25 の間隔で層に分けた場合の、0 を中心としたプラスマイナス方向への層の順番を示します。1 は[0,0.25], 2 は [0.25,0.5] また -1 は[-0.25,0]、-2 は[-0.5,-0.25]を示します。但し、両端の層は、片側が±∞） 

一見して分る通り、無作為抽出で得られたサンプル数の度数分布は、標準正規分布からは、どうしても偏りが出ます。サンプル数を ∞ に向けて増やしていけば、標準正規分布のきれいなカーブに近づいて行きます。しかし、有限個の場合は、サンプル数の偏りが発生するのは、避けられません。 

これを、層別サンプリング法により、各層で生成されるサンプル数を、各層の確率測度に比例した数だけ生成すると、下図のようになります。一見して分る通り、分布の偏りが大きく改善されます。（あくまで、分布の全体像を示すためだけの例なので、目盛りは無視して下さい。） 

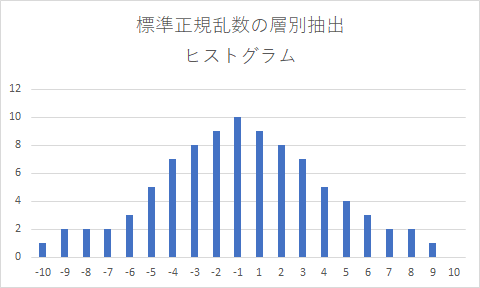
無作為抽出の方法で見られる、サンプル分布の偏りは、サンプル平均に誤差を生じさせる大きな原因になります。例えば、オプションの Payoff で In the Money の領域に、対象資産価格のサンプルがより多く偏った場合、サンプル平均は、真の平均より大きくなるでしょうし、逆に、Out of The Money の領域にサンプル数が多く偏った場合、小さくなるでしょう。しかし、それを、層別抽出法でサンプルを生成すれば、モデルが想定している分布に近い分布でサンプルを生成する事ができ、サンプル数の領域間（層別間）の偏りによる誤差を小さく（殆ど消す事が）できます。これが、層別抽出法による推定誤差の低減効果です。 

さらに、各層へのサンプル数の配分を、確率測度に比例させず、恣意的に行う事で、より大きな分散低減効果を得る事も可能です。例えば、シンプルなヨーロピアンオプションの Payoff の場合、対象資産の価格分布の領域をいくつかの層に分けた上で、In the Money の領域の層のサンプル数を、より多く配分し、Out of The Money の領域にある層のサンプル数をより少なく配分すれば、同じサンプル数であっても、より高い分散低減効果を得る事ができます。もう少し、精確に言えば、各層における Payoff の予想期待値を、事前にシミュレーションで求めておき、その期待値が大きい層に、より多くのサンプルを配分し、期待値が小さい層に、より少ないサンプルを配分します。Deep Out of The Money の層であれば、Payoff の期待値は 0 になり、そういった層には、ほとんどサンプルを配分しなくても、シミュレーション上は問題ありません。分散に影響を与えるのは、In the Money でかつ確率測度の高い領域であり、そういった領域へのサンプル数を、恣意的に多くすれば、より大きな分散低減効果が得られます。 

層別にサンプルを生成する方法は、モデルを駆動する乱数の分布関数が解析的に求まっていれば、通常の乱数生成のアルゴリズムを少し修正するだけで、簡単に出来ます。乱数生成のアルゴリズムは、まず一様乱数の生成からスタートしますが、一様乱数のサンプルの層別生成は極めて簡単です。そうやって層別抽出された一様乱数を、分布関数の逆関数を使って標準正規乱数に変換すれば、標準正規乱数自体を層別抽出した事になります。一方、分布関数が解析的に求まっていない場合、受理棄却法などの方法を使えば、層別にサンプルを生成できますが、無駄になる乱数生成が多く発生し、計算時間の増加が、推定誤差低減効果を減殺してしまいます。 

次のセクションで、サンプルの層別抽出法を具体的に解説したいと思います。その後で、層別抽出法による推定誤差の低減効果がどの程度になるか、またサンプル数に偏りを持たせる場合、どのようにすれば最も推定誤差が低減できるのかについて、解説したいと思います。 

6.6.4.4.2　  層別のサンプル抽出法

LMM のように、確率変数がブラウン運動で駆動される場合、層別サンプリング法を使うには、まず標準正規乱数を層別にサンプル生成する必要があります。その層別化された乱数を LMM 等のモデルに代入すれば、そこから導出される確率変数（フォワードLiborなど）自体が層別にサンプル生成された事になります。さらに、Libor に依存する Payoff の値も層別化された事になります。 

そこで、標準正規乱数の層別サンプリング法ですが、そもそも、コンピューターアルゴリズムで生成される標準正規乱数は、一様乱数を変換したものです。従って、一様乱数を層別にサンプル抽出し、それを標準正規乱数に変換すればいいだけです。一様乱数を層別化するのは極めて簡単です。 

コンピューターアルゴリズムでの一様乱数の生成方法は既に説明しました（Section 6.6.3.1）。生成される一様乱数は \([0,1)\) の値域でランダムな値を取るのでした。そこで、\([0,1)\) の領域を、互いに交わらない n 個の区間　\(A_i,~~i=1,…,n\)　に分割し、それぞれの区間で　\(m_i\) 個、合計で Ｍ個の一様乱数を生成するとします。\(A_i\) 層で生成された一様乱数を \(\dot {u}_{i,j},~~~j=1,…,m_i\) と表記します。以上を数式で記すと、 

\[ \begin{align} & A_1=[0,a_1)~~~~A_2=[a_1,a_2),…,A_n=[a_{n-1},a_n =1), \\ & \bigcup A_i =[0,1),~~~~A_i∩A_j=\emptyset \\ & \dot {u}_{i,j}=\{ \dot {u}_{i,1},…,\dot {u}_{i,m_i}\} \in [a_{i-1},~a_i ) \\ & M=\sum_{i=1}^n m_i \end{align} \]

層別化は、各層の確率測度を均等に区分してもかまわないし、それぞれ任意の幅に取ってもかまいません。そのようにして層別化された各層に、それぞれの確率測度に比例する数の一様乱数を生成して配分します。その方法は、まず \([0,1)\) 間の一様乱数 u を M 個生成した後、下記式を使って、\([a_{i-1},~a_i)\) 間の一様乱数に変換するだけです。 

\[ \dot {u}_{i,j}=a_{i-1}+(a_i-a_{i-})u,~~~~~ i=1,…,n ~~~~ j=1,…,m_i \tag{6.94} \]

各層の内部だけで見ると、\(\dot {u}_{i,j},~~~~ j=1,…,m_i\) はそれぞれ独立で、無作為抽出したのと同じように層内で散らばります。 

ちなみに、[0,1) 間の一様乱数を無作為抽出した場合に、各区間に一様乱数 u が含まれる確率　\(P_i\)　は、 

\[ P_i \left(u∈[a_{i-1},a_i )\right)=a_i-a_{i-1}~~~~~~i=1,…,n \]

となります。これは、各層に含まれるサンプル数 \(m_i\) の、M に対する比率の期待値 \(E(m_i/M)=P_i (u∈[a_{i-1},a_i ))\) でもあります。単なる無作為抽出では、すでにグラフで示した通り、\(m_i/M\) と \(P_i\) は必ずしも一致しませんが、層別サンプリング法は、それが確実に一致するようにサンプルを生成するものです。 

さらに層別サンプリング法は、 \(m_i\) を確率測度に比例させずに決める事も可能です。その場合、区間 \(A_i\) に属するサンプルの条件付き期待値を計算する際に、確率測度の補正が必要になります。すなわち、各サンプル値に下記の補正値 \(R_i\) を掛けて補正する事になります。これについては、後ほど、より詳しく説明します。 

\[ R_i=\frac {P_i}{m_i/M} \tag{6.95} \]

注： \(R_i\) は、尤度比（likelihood ratio）と呼ばれ、連続な確率測度間のラドン・ニコディム微分に相当します。離散的なデータの確率測度の変換なので、微分ではありませんが、役割は同じです。 

さて、以上のように層別抽出された一様乱数を、標準正規分布関数の逆関数に代入すると、層別化された標準正規乱数に変換できます。
まず、一様乱数の各層を標準正規分布関数の逆関数を使い、標準正規分布の層に変換します。すなわち、 

\[ \begin{align} & A_1~~→~~Z_1=[Φ^{-1} (0),Φ^{-1} (a_1 )), \\ & A_2~~→~~Z_2=[Φ^{-1} (a_1),Φ^{-1} (a_2)),… \\ & A_n~~→~~Z_n=[Φ^{-1} (a_{n-1}),Φ^{-1}(a_n )) \end{align} \]

そして、各層ごとに生成された一様乱数も同様にして標準正規乱数に変換します。 

\[ \dot{x}_{i,j}=Φ^{-1}(\dot {u}_{i,j}) \tag{6.96} \] \[ \dot {x}_{i,j}=\{\dot {x}_{i,1},…,\dot {x}_{i,m_i} \}∈[Φ^{-1}(a_{i-1}),Φ^{-1}(a_i)) ~~~~~~~~~~~~~~~~~(6.96)' \]

\(Φ^{-1}(∙)\) は単調増加関数なので、\(A_i\) 層で抽出された一様乱数はすべて、\(Z_i\) 層に入ります。また、\(Z_i\) の各層の確率測度も、\(A_i\) の確率測度と一致します。図示すると、こんなイメージです。 

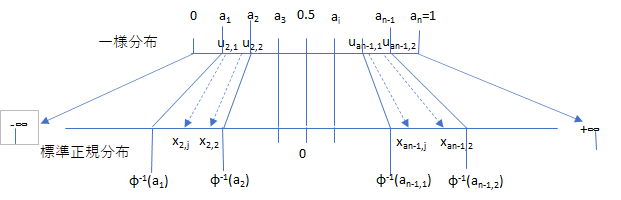
標準正規分布関数の逆関数 \(Φ^{-1}(∙)\) は、実際には近似式ですが、有効数字の桁数が ９～１３程度と、極めて精確な近似式なので、金融の分野でのMCSで使うには、これで十分かと思います。 

さらに、この層別化された標準正規乱数を古典的 LMM に代入して、フォワード Libor をシミュレーションすると、フォワード Libor の分布自体が層別化されたことになります。図示すると、こんなイメージです。 

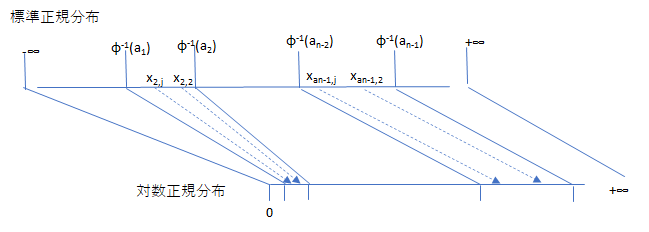
古典的 LMM はフォワード Libor が対数正規分布すると仮定しているので、値域は \([0,∞)\) になります。 

さらに、実際に求めたいサンプル平均は、Libor を対象としたデリバティブズの Payoff 関数値です。という事は、Payoff の関数値を層別化する必要がありますが、上記の説明と同様、一様乱数の層別化から順次変換していけば、最終的に Payoff 関数値が層別化された事になります。Payoff 関数を ｙ（） と置くと、ｙ は、その元の元となる一様乱数の関数とみなせ、\(y(\dot {u}_{i,j})\) と表記できます。あるいは、標準正規乱数 ｘ の関数として、\(y(\dot {x}_{i,j})\)　とも表記可能です。 

6.6.4.4.3   各層の条件付き期待値と、その確率加重平均

サンプル値の値域を層別化する事によって、いかにサンプル平均の推定誤差を小さく出来るか見てみます。その前に、そもそも層別サンプリング法を使った場合の、サンプル平均の求め方を説明します。既に簡単に述べましたが、確率変数全体の期待値は、層別化した場合、各層での条件付き期待値の確率加重平均で求まります。 

まず、層別サンプル数を、各層の確率測度に比例して生成する場合を考えます。この場合、各層の確率測度は解析的にすでに求まっているとして、それを \(P(x∈A_i)=P_i\) と表記します。ここでは、標準正規乱数 x を層別化したと考えます。求めるサンプル値は、x の関数として \(y(x)\) と表記します。 

確率測度に比例して層別サンプルを生成するので　\(P_i=m_i/M\) とならないといけないのですが、\(m_i,~M\) は整数なので、\(P_i=m_i/M\) となるよう各層の範囲（すなわちPiが、有理数になるような範囲）を決めなければなりません。そして \(y_{サンプル平均}\) を サンプル全体の平均とすると、 

\[ y_{サンプル平均} \approx E(y(x))=\sum_{i=1}^n P_i~E(y(x)|x∈A_i ) \tag{6.97} \] \[ y_{サンプル平均} = \sum_{i=1}^n P_i∙ \frac {1}{m_i} \sum_{j=1}^{m_i} y(\dot {x}_{i,j}) =\sum_{i=1}^n \frac {m_i}{M} \frac {1}{m_i} \sum_{j=1}^{m_i} y(\dot {x}_{i,j}) =\sum_{i=1}^n \frac {m_i}{M} y_{i層平均} \tag{6.98} \]

但し　\(y_{i層平均}\) は、\(\dot {x}_{i,j}\) が \(A_i\) 層に含まれている場合の条件付きサンプル平均です。 

各層のサンプル数を恣意的に決めた場合は、6.95 式の尤度比（likelihood ratio）を使って各層の確率測度を補正すれば、同様に全体のサンプル平均が求まります。すなわち 6.98 式にある確率測度 \(P_i\) に、尤度比\(R_i\) を掛けて、下記式のようにして求めます。 

\[ y_{サンプル平均} = \sum_{i=1}^n P_i ∙ R_i∙ \frac {1}{m_i} \sum_{j=1}^{m_i} y(\dot {x}_{i,j}) =\sum_{i=1}^n P_i ∙ \frac {P_i}{m_i/M}∙ y_{i層平均} \tag{6.99} \]

ここで使われた尤度比　\(\frac {P_i}{m_i/M}　は、確率測度変換におけるラドン・ニコディム微分に相当します。（有限個の離散的なデータを使うので、ラドン・ニコディム微分とは呼べませんが、その役割は同じです。）