1. QuantLibを使ってみる
1.2 Example を試す
1.2.5 CallableBonds : Call Option付き債券の価格評価
1.2.5.1 はじめに
固定金利債で、Call Option や Put Option が付いているものは、政府債ではあまりみかけませんが、事業債では一般的です。債券の Call Option とは、発行体が、任意で債券を中途償還できる権利であり、Put Option は逆に投資家側から中途償還を請求できる権利です。発行体は、調達金利が低下してより安いコストで借換えができる場合に、Call Option を行使します。一方、投資家は、金利が上昇して、同質のクレジットで、より高い利回りの投資が可能になれば、Put Option を行使して、投資対象を乗換える事ができます。
事業債の利回りは一般的な市場金利に加え、発行体のクレジットスプレッドの影響も受けるので、Call Option は、厳密には、“金利” と “クレジットスプレッド” が確率変数となるオプションになります。(Put Option もそうです。) 従って厳密な価格計算をしようとすると、両方の確率変数を勘案したモデルが必要になりますが、実務慣行としては、金利オプションの部分にのみ着目したモデルで価格評価を行うのが一般的です。債券の場合、まず市場価格が与えられます。そこから、何等かの金利オプションモデルを使って債券価格に含まれるオプション価値を推定します。そのオプション価値を、市場価格から差し引いた後の利回りとクレジットスプレッド(OAS:Option Adjusted Spread)を計算し、一般的な投資家は、それを投資判断の基準としています。
この場合クレジットスプレッド・オプションの価値は勘案されていません。すなわち、クレジットスプレッドは将来に渡り一定、と仮定されている事になります。クレジットスプレッドオプションの価値の計算は、クレジットスプレッドの変動が、例えば CDS(Credit Default Swap) 市場などでスプレッドの変動が観測できる銘柄に限られるので、大半の事業債では、計測が不可能です。また、クレジットスプレッドは金利水準と異なり、短期的には比較的安定しているので、その変動リスクを、あまり厳密に勘案しなくても良いだろうという思いもあるでしょう。
ところで、この Example では、OAS を計算するアルゴリズムをテストするのではなく、デリバティブズの価格計算と同じように、パラメータを外生的に与えて、そこから価格計算する方法をテストしています。すなわち、市場価格を外生的に与える事なく、債券価格自体を、モデルから導出しています。QuantLib のライブラリーを覗くと、OAS を計算するメソッドも備わっているようです。いずれにしても、Call Option 付きの固定金利債券の金利オプション価値をどのように計算するかが重要なので、そこにフォーカスして説明したいと思います。
また、この Example でテストする商品オブジェクトの CallableFixedRateBond クラスや、価格エンジンの TreeCallableFixedRateBondEngine クラスは、ソースコードが格納されているディレクトリ名が experimental(実験用?) となっています。どうも β 版のようなもので、これをそのまま完成版として使うべきではないので注意して下さい。実際にソースコードを覗くと、コールオプションの行使期日と、債券のクーポン日の関係性のチェックを、債券の具体的な情報を使わずに、ハードコードで無理やり行っている部分がありました。知らずに使うと問題を起こす可能性があります。
コードを理解するには、最低限Hull-Whiteモデルの概要を理解している事が必要です。その前提で話をすすめさせて頂きます。(Hull-Whiteモデルについては、上級編“Hull-Whiteモデル”の所で、解説しています。)
1.2.5.2 ソースコードのコンパイルと実行
まず、これまで通り、ソースコードのビルドの方法から説明します。QuantLibのインストール方法を解説したセクションですでにビルドしていれば、再ビルドは必要ありません。もし、ビルドが済んでいない場合は、次の手順で、Debugモードでビルドし、試しに実行してみて下さい。
- QuantLibのファイルFolderのExampleディレクトリから、CallableBondsのディレクトリを探し、そこにあるプロジェクトファイル CallableBonds.vcxproj をダブルクリックし開ける。Visual Studio が起動され、このプロジェクトファイルが開かれます。
- ソリューションエクスプローラーに表示されているプロジェクトのディレクトリを展開し、SourceFiles のフォルダーにある "CallableBonds.cpp" をクリックする。約350行あるソースコードが開かれます。
- 3. きちんと動作するか、まず確認してみる。メニューバーからビルド→ソリューションのビルドを選択。ビルドが開始されます。既にビルド済みであれば、この操作は必要ありません。(当初、複数のプロジェクトをまとめているQuantLib.slnをビルドした場合、個別のプロジェクトにおけるmain()関数を走らせる必要があります。その場合は、ソリューションエクスプローラーwindowから、該当のプロジェクト(ここではCallableBonds.)をクリックした上で、メニューバーから “プロジェクト” → “スタートアッププロジェクトに設定” を選択して下さい。)
- エラー無くビルドが正常終了すれば、試しにプログラムを走らせてみます。メニューバーのデバック→デバックの開始を選択。下記の Console画面が出力されれば成功です。(但し、プログラムが終了すると同時に Console画面も消えてしまうようであれば、メニューバーから、 ツール → オプション → デバック → 全般 を選択し、「デバックの停止時に自動的にコンソールを閉じる」のチェックボックスをはずします。)
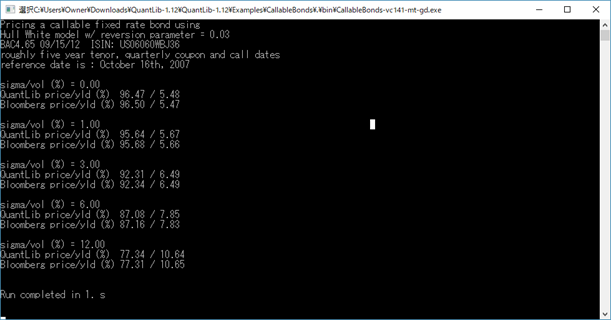
- 5. 下記のConsole画面にある通り、この例ではCallable Bondsを、5通りのVolatility値でシミュレーションし、それをBloombergの計算結果と比較しています。計算時間は、私のPCで1秒程度でした。3項Treeを使った数値解の計算アルゴリズムを数回走らせていますが、結構早い印象です。
1.2.5.3 ソースコードの解析
< プログラムコードの全体像 >
まずプログラムコードの全体像を俯瞰してみます。
このExampleでも、これまでと同様、次の様な手順でコードが書かれています。
- まず、Instrument (商品オブジェクト)と PricingEngine (価格エンジンオブジェクト)の部品を生成します。
- 次に、それらを組み立てて、価格エンジンと商品のインスタンスを作成します。
- 最後に、価格エンジンを商品オブジェクトに設定した後、商品オブジェクトに備わっている cleanPrice() と yield() メソッドを走らせて、価格と利回りを計算しています。
金利オプション価値の計算には、Hull Whiteモデルをもとに、3項Treeを使っています。モデルに投入するVolatilityの値を5通り用意し、それぞれの計算結果を、Bloombergの計算結果と比較しています。上記のConsole画面出力の通り、概ね、近い値が出ているのが判ります。Hull-Whiteモデルを使っているので、シナリオにあるVolatilityは、ガウス分布における瞬間短期金利のVolatilityであり、Black Modelで使われる対数正規分布のVolatilityではありません。そうすると、金利の(変化率ではなく)絶対水準が、1年で(1×標準偏差の信頼区間で)上下3%~12%変動するとの最後の3つのシナリオは、あまり現実的ではありません。このExampleは、プログラムコードのテスト目的なので、むしろ極端なパラメータを使った方が、問題を発見しやすいので、そうしたのかも知れません。
< ステップ毎のコード解析 >
では、Exampleのコードを、ステップ毎に説明します。
① 事前準備
51~77行目において、このExample専用のメソッドとしてflatRate( )という、フラットなイールドカーブ(YieldTermStructureインスタンスへのポインタ)を返すメソッドが定義されています。異なる引数の型に対応する為、同じメソッド名で2つのオーバーロード関数が実装されています。それぞれ、後でmain( )関数の中で使われていますが、このExample用だけに定義されている関数なので、QuantLibのライブラリーにある別のクラスから呼び出して使う事は出来ません。
② boost::timerのセット
79行目から main( ) 関数がスタートします。
まず 83行目の boost::timer は、これまでと同じく、この Example の実行にかかる計算時間を計測します。上の Console 画面出力の通り、この Exampleでの計算時間は、たかだか1秒でした。
③ 本日の日付と、時価評価基準日(evaluation date)の設定
85 と 86行目で、本日の日付と、Evaluation Date の設定を行っています。本日を 2006年10月としており大分古いですが、テスト上は問題ありません。この Example コードがかなり昔に作成された事を伺わせます。Evaluation Date は 87行目にある通り、本日と同じ日で設定されています。前の Bonds の Example では、取引慣行に従い、債券の決済日を Evaluation Date としていました。この違いにより、微妙な価格差が発生します。実務では、どちらの基準日で時価評価しているのか、注意が必要です。
④ イールドカーブの構築
108~116行目でイールドカーブオブジェクトを生成しています。ここでは5.5%のフラットなイールドカーブを生成しています。事前準備で用意したflatRate( )メソッドを使っています。債券の利回り表示は、一般的な市場慣行では、フラットなイールドカーブを前提としたIRR(内部収益率)の概念を使って行うので、このような設定にしたのだと思われます。
⑤ 金融商品オブジェクトの部品の生成
120~164行目で、価格評価の対象となるCallable Bondの部品と属性データを生成しています。ここで生成される商品オブジェクトはCallableFixedRateBondクラスのインスタンスです。このクラスの階層構造は以下のようになっています。左に行くほど、抽象的なベースクラスになります。
LazyObject ← Instrument ← Bond ← CallableBond ← CallableFixedRateBond
クラス名から判る通り、ここでは固定金利クーポンのコールオプション付き債券を構築します。固定金利クーポン債券の構築の仕方については、前の Bonds の例で説明しました。再度、簡単に説明すると、固定金利キャッシュフローの正確な日付と金額を特定するための情報をもとに、商品オブジェクトを組み立てます。ここでは、141から164行目で、その部品・情報を用意しているのが判ります。債券の発行日、償還日、クーポンレート、支払い回数、日数計算方法、カレンダー、休日の取扱い慣行、などです。
特に、キャッシュフロー日付けを特定する Schedule クラスのインスタンスが、大きな部品として生成されています(162行目)。また、キャッシュフロー金額は、Scheduleオブジェクトを使って、この債券のコンストラクターの中で構築されています。これらについても Bondsの例のなかで詳しく説明しているので、そちらを参考にして下さい。
さて、CallableBond オブジェクトは、通常の債券の情報に加え、Call Option ・ Put Option の行使日と行使価格の情報が必要です。120 から 136行目で、その情報を持つ CallabilitySchedule オブジェクトを生成しています。このクラスは、Callability オブジェクトの配列です。Callability オブジェクトは、それぞれ一個のオプションの情報をカプセル化しています。具体的には、Put/Callのタイプ、償還価格(すなわち行使価格)、および行使日の情報です。この例では、各クーポン日にオプション行使が可能となっているので、合計で 24回のコール日付が設定されています。従って、それぞれに対応する24個の Callability オブジェクトが生成され、それが CallabilitySchedule 配列に格納されています。
⑥ 金融商品オブジェクトの生成
以上で用意された部品・情報をもとに(即ちコンストラクターの引数として渡す事により)、181行目で CallableFixedRateBond のインスタンスが生成されています。これで、金融商品オブジェクトが完成です。
⑦ 価格エンジンの部品の生成
Callable Bond は Call Option の付いた債券であり、その価格計算には何等かの金利オプションモデルが必要になります(固定金利債の場合だけです。変動金利債の Call Option は一種のクレジットスプレッドオプションで、全く別体系のオプションモデルが必要になります。固定金利債であっても事業債であれば、クレジットスプレッドオプションの要素が含まれていますが、この例では考慮されていません)。ここでは Short Rate Model の代表格である Hull-White モデルが使われています。Callable Bondの場合、通常 Call Option が複数回存在しており、いわゆる Bermudan Option の形態をとるものがほとんどです。従って、解析解で価格計算を行うのは望み薄です。そこで、何等かの数値解を求めるアルゴリズムが必要になります。Hull-White は、3項 Tree を使って、アメリカンや バージョンのオプション価格を計算する方法を提示しており、ここでもその方法が使われています。
では、ソースコードを見てみます。価格エンジンの部品となる HullWhite(Model)オブジェクトを組み立てる為、まず部品の部品を用意します。166 から 173行目で、3項 Tree を使った HullWhite(Model)に必要なパラメータを準備しています。失礼しました。166 と 167行目の maxIteratinos 変数(1000に設定されている)および accuracy 変数(小数点で8桁)だけは、HullWhite(Model) とは関係ないパラメータです。このパラメータは、後で CallableBond クラスの yield( )メソッドの引数として使われます。そのメソッド内で使われる Solver の、再計算回数の上限と、求める利回りの精度を設定する値です。
168 行目の、gridIntervals 変数(40に設定)は、3項Tree の時間軸方向のステップ数を設定します。また reversionParameter (0.03に設定)は、HullWhite(Model) のドリフト項における中心回帰強度を設定します。173 行目は volatility 値を、とりあえず適当な値で初期化しています。後で、この値を変えながら、価格に対するインパクトをシミュレーションします。本来、中心回帰強度と Volatility は、市場データに Calibration して導出されますが、ここでは無理やり外生的に与えています。あくまでテスト用のプログラムなので、Calibration はテストの目的外という事なのでしょう。(Hull-Whiteオブジェクトの詳細な説明については、次の Example “Gaussian 1D Short Rate Model” の例で説明する予定です。)
そして 175 行目で、HullWhite(model) クラスのコンストラクターに、中心回帰レベルを決めるイールドカーブ(termStructure)と中心回帰の強度(reversinParameter)、および Volatility(sigma)を与えて、HullWhite(model)クラスのインスタンスを生成しています。
⑧ 価格エンジンオブジェクトの生成
価格エンジンの部品(と言ってもHullWhite(Model)オブジェクトだけですが)が揃ったので、178行目でそれらを使って、TreeCallableFixedRateBondEngine を生成しています。この価格エンジンが、3項 Tree を使った Callable Bond の価格計算機能を備えており、その Tree の時間間隔を生成するのに必要な、もうひとつのパラメータ gridIntervals (ここでは 40 に設定)をコンストラクターに渡しています。これで価格エンジンが出来ました。実際の価格計算アルゴリズムは、相当複雑なので、ここではあえて説明しません。QuantLibライブラリーを、ありのままで使おうとされるユーザーであれば、商品オブジェクトと対応する価格エンジンの構築方法、および、用意されているインターフェースの機能さえ理解しておけば十分でしょう。さらに応用したいという方は、自らソースコードで確認してみて下さい。
⑨ 商品オブジェクト(Instrument)に価格エンジン(PricingEngine)を設定後、価格と利回りを計算
185 行目で、CallableBond オブジェクトに、TreeCallableFixedRateBondEngineを設定しています。
これまでの Example では金融商品(Instrument)クラスに備わっている NPV( )メソッドを呼び出して、金融商品の現在価値を計算し出力していました。ここでは、Bond クラス特有のメソッドを使って価格を計算し出力しています。すなわち、195 行目にある cleanPrice()メソッドです。NPV( )メソッドは、債券の将来キャッシュフローの現在価値合計を計算しますが、そこには経過利息の価値も含まれます。いわゆる Dirty Price と呼ばれているものです。債券の場合、一般的に市場でQuoteされている価格は、Clean Priceと呼ばれる、経過利息を除いた価格になります。経過利息の計算方法は、債券の種類や、取引市場によって様々であり、個別の債券の種類ごとに特定する必要があります。計算方法は、Bondオブジェクトを構築する際に、引数として渡した、日数計算方法や、カレンダーや、休日の取扱い方法などで決まっていきます。181行目で、Callable Bond の商品オブジェクトを生成する際に、コンストラクター へ渡された引数のいくつかは、それを計算する為です。
187 行目以降は、Hull-White モデルの Volatility パラメータを様々に動かしながら、Callable Bond の価格を計算し、その計算結果を Bloomberg の計算結果と比較しています。注意して見て欲しい点は、Volatility パラメータを動かすごとに、新しい Hull-White モデルのインスタンスと、それを使った3項 Tree の価格エンジンを生成している事です。Black-Scholes モデルを使った株式オプションの価格エンジンでは、Volatility 情報は、一種の市場データとして Observable として価格エンジンに与えられていました。Volatility データが変更になった場合は、Observer パターンに従い、データ変更の通知が価格エンジンに送られ、価格エンジンが必要に応じて再計算する仕組みでした。すなわち、都度価格エンジンを生成する必要はありませんでした。しかし、ここでは、Hull-White モデルに与えられたVolatility は、Observableではなく、単に実数値として与えられているので、その値が変更になると、オプションモデルさらに価格エンジンを作りなおさなければなりません。3項Treeを使う場合、Volatilityが変わると、Tree構造全体をすべて書き替えないといけないので、そうなっているのでしょう。
以上で、このExampleの説明は終わりです。
<ライセンス表示>
QuantLibのソースコードを使う場合は、ライセンス表示とDisclaimerの表示が義務付けられているので、添付します。 ライセンス