1. QuantLibを使ってみる
1.2 テストプログラムを試す
1.2.3 MulticurveBootstrapping : Multi-Curve の構築
1.2.3.4 ソースコードの解析
ソースコードの本体部分について、次のような順番で解説します。
- 時価評価基準日の設定
- Discount curve(OIS curve)の構築
- Index curve(forecasting curve)の構築
- Instrument オブジェクト(金利スワップ)の組み立て
- PricingEngineの組み立て、価格の計算、画面出力
- Appendix 1~5 重要なクラスの解説
行番号を付したhtmlファイルに変換したソースコードを載せますので、それを見ながら、読み進めて下さい。
1.2.3.4.1 時価評価基準日の設定 (63~83行目)
まずmain()本体の最初に、下記のようなデータが与えられています。
| ・ 使用されるCalendar (67行目) | : TARGET |
| ・ 本日(todaysDate)(69) | : 2012年12月11日 |
| ・ 時価評価基準日(Settings::instance().evaluationDate()) (70) | : 本日 |
| ・ 本日から決済日までの日数(fixingDays) (73) | : 2営業日 |
| ・ 決済日(settlementDate; スワップのスタート日)(76) | : 本日+2営業日 |
この内、時価評価基準日は、通常、すべての商品の価格計算で必要な情報なので、グローバル変数として取り扱われるべきデータになります。QuantLibでは、そのようなデータを保持するため、Settingsクラスを用意しています。このクラスは、Singleton パターンを使い、グローバルな変数が、一個だけしか生成できないようにしたクラスです。ここでは、時価評価基準日としてtodaysDateをSettingsオブジェクトの中に設定しています。
(注:Settingsクラスについては、マルチスレッドの環境下で使うと、問題含みです。その辺りについては、ここでは解説しません。Luigi Ballabio氏のImplementing QuantLib : Odds and End 中で、詳しく解説されているので、それを参照して下さい。その該当箇所の日本語訳はこちら。)
1.2.3.4.2. Discount Curve(OISカーブ)の構築 (85~201行目)
次に、1 本目のイールドカーブとして、EONIA(Euro Over-Night Index Average)インデックスをベースにした OIS カーブを組み立てます。
注 : ユーロのOvernight Indexは、このプログラム例が作成された当時はEONIAでしたが、その後ESTRに変更されています。
注 : プログラム例のコードを理解するために、ここでイールドカーブ生成のアルゴリズム(Boostrapping+Interpolation法)を復習しておきましょう。その手順を簡潔に述べると、
- 指標金利の観測点となる期間(pillar)を満期とするベンチマーク商品(インターバンク預金や、FRAや、金利先物や、金利スワップなど)を特定し、その市場レートを取得する。
- そのベンチマーク商品のキャッシュフローから、Discount Factor を未知数とする、次のような方程式を立てる。
\( \sum \left(CashFlow_i \times DiscountFactor(t_i)\right) = MarketPrice \)
(商品の市場価格は、デリバティブズであれば右辺は 0, 債券や預金も、決済日のCash Flow(市場価格に相当)も上記左辺に含めて計算すれば やはり右辺は 0)
- ii. の方程式をすべての期間(pillar)で設定し、それを連立させ、
- その連立多元方程式を解く形で、未知数となる Discount Factor ベクトルを求める事になります。(詳しくは基礎編:イールドカーブの構築方法(2))
QuantLib では、上記の
i. の役割を Quote クラスのオブジェクトが行い、
ii. の役割を、BootstrapHelperクラスのオブジェクトに担わせ、
iii. それを期間(pillar)の順で並べて(配列を作り)、
iv. その配列を部品として、PiecewiseYieldCurve < Discount, Cubic,… > オブジェクトを構築し、そこで連立方程式を解くアルゴリズムを走らせます。
このステップを念頭に、ソースコードを見ていきます。
(1) 基礎的な部品:まず基礎的な部品の生成から
-DayCounterオブジェクト(89行目) :
イールドカーブ構築の際に使われる日数計算方を、ここでは Actual365Fixed に設定しています。
-BootstrapHelper オブジェクトの配列変数(90行目) :
上記 ③のBootstrapHelper の配列を格納する配列変数(変数名 eoniaInstruments)を生成。この段階ではまだ空です。
-OIS インデックス(92行目) :
OISインデックスとしてEoniaクラス(Indexクラスの派生クラス)のオブジェクトを設定。
(2) ベンチマーク商品ごとにBootstrapHelperオブジェクトの生成(105~190行目)
ここでは下記の3種類のベンチマーク商品の市場データを使い、それぞれについて、BootstrapHelperオブジェクトを作成します。(BootstrapHelper<YieldTermStructure > クラスについては Appendix-4 で解説)
-オーバーナイト金利(105~123行目) :
Overnight(本日から翌営業日)、Tomorrow Next(翌営業日から翌々営業日)、Spot Next(翌々営業日から1営業日後)の3種類のオーバーナイト金利を使って、イールドカーブの最も手前の部分を構築します。
- まずそれぞれの市場金利データから Quote オブジェクトを作成します(105~110)。上記で説明したアルゴリズムの i. のに相当します。
(注:Quoteクラスについては、Appendix-1、そのベースクラスであるObservableクラスについてはAppendix-2) - それに、いくつかの小さな部品を加えて、BootstrapHelper(ここではその派生クラスの DepositRateHelper クラスの)オブジェクトを作成します(114~123)。これは上記アルゴリズムの ii. に相当します。
(注:Quoteオブジェクトのポインタを使って、Handle< Quote> オブジェクトを作成し、それを BootstrapHelper に渡しています。Handle についてはAppendix-3) - 作成された BootstrapHelper オブジェクトは、eoniaInstruments という名の配列変数に格納されます(122行目、for ループの中)。これは上記アルゴリズムの iii. に相当します。
-先日付スタートの短期OIS(142~159行目):
- フォワードOIS期間(スタートとエンド日)と、それに対応するレートのデータが与えられて、Quote オブジェクトを生成しています(145~149)。ちなみに、このスワップ期間は、欧州中銀による、準備預金モニタリング期間に対応しています。
- その Quote オブジェクトと、さらにいくつかの小さな部品を加えて BootstrapHelper (ここではその派生クラスの DatedOISRateHelper<YieldTermStructure>クラスの)オブジェクトを作成します(152~159)。
- 作成されたこの BootstrapHelper オブジェクトも、eoniaInstruments に格納されます。
- 中長期のOIS(163~190):
- 期間が 15か月から 30年までの中長期 OIS レートを使って、18 種類の Quote オブジェクトを生成します(163~182行目)。
- さらに、その Quote オブジェクトにいくつかの小さな部品を加えて BootstrapHelper(ここではその派生クラスの OISRateHelper<YieldTermStructure>クラスの)オブジェクトを作成します(184~190行目)。
- これも、eoniaInstruments という名の配列変数に格納されます。
さて、以上で、Boostrapping + Interpolation アルゴリズムの i. から iii. のステップが完了しました。最後の iv. のステップが次にきます。
(3) YieldTermStructure オブジェクトの作成(194~201行目)
上記で生成された BootstrapHelper の配列(eoniaInstruments)を使って、PiecewiseYieldCurve<Discount、Cubic,…>オブジェクトを生成します。このステップは簡単で、部品をそのコンストラクターに渡すだけです(194~195)。コンストラクターを起動すると、Boostrapping+Interpolation アルゴリズムが走り、iv. の連立方程式を解いて、イールドカーブ(ここではDiscount Curve)が完成します。
(注 : PiecewiseYieldCurve<Discount、Cubic,…>はクラステンプレートで、3 種類のテンプレート引数を取ります。但し、3 番目の引数はデフォールト設定されているので、194行目のコードでは省略されています。このオブジェクトは、テンプレート引数 Discount で指定された YieldTermStructure の派生クラスのオブジェクトになります。これについては Appendix-5)
さらに、出来上がったYieldTermStructure オブジェクトのポインタを使って、RelinkableHandle<YieldTermStructure>オブジェクトを生成しています。これはHandle クラスの派生クラスで、ポインタのポインタになります。
これで、OIS カーブが出来上がり、PricingEngine へ渡す準備も整いました。
1.2.3.4.3. Index カーブ(forecasting カーブ)の構築 (208~307行目)
2本目のカーブとして、スワップの変動金利キャッシュフローを推定する為のイールドカーブを組み立てます。このカーブはInstrumentの部品になります。組み立ての手順は、OISカーブと同じで、
- 期間(pillar)ごとのベンチマーク商品と、その市場レートを Quote に格納し、
- それを使って商品ごとの BootstrapHelper を作成し
- それを配列変数に格納し
- その配列変数を、PiecewiseYieldCurve<Discount, Cubic,...>のコンストラクターに渡し、Boostrapping + Interpolation のアルゴリズムを走らせます。
繰り返しになるので、コードの解説は省略しますが、OIS カーブとの違いだけ示しておきます。
- 指標金利インデックス(210行目) : OIS カーブの時は、Eonia インデックスを使いましたが、ここでは Euribor6M イ ンデックス(期間6か月のEuribor金利)を使っています。
- ベンチマーク商品として FRA を使う(226~254行目) : FRA をイールドカーブ構築の為のベンチマーク商品としています。そのため BootstrapHelper は、FraRateHelper を使っています。
- ベンチマーク商品として Euribor の金利スワップを使う(258~293行目) : OIS では、中長期ゾーンのベンチマーク商品として OIS スワップを使いましたが、ここでは Euribor の金利スワップを使っています。従って、BootstrapHelper として SwapRateHelper を使っています。
生成されたイールドカーブのオブジェクトは、さらに RelinkableHandleオブジェクト(変数名forecastingTermStructure)に格納され、それが PricingEngine の部品となります(306~307行目)。
(注 : Euribor や Libor は、指標金利としての役割を終え、新たに、これらを指標金利とするデリバティブズ取引を新規で取り組む事は無いと思います。但し、業界内には過去の取り組んだ長期のスワップ取引が、相当数残っており、それらの時価評価には、forecasting カーブとして、Euribor や Liborを指標金利とするイールドカーブを構築する必要があります。この場合、各通貨のOISフォワード金利に、それぞれ決まった固定スプレッドを足して、カーブを構築します。)
以上で、2種類のイールドカーブが組み立てられました。
1.2.3.4.4. Instrument オブジェクト(金利スワップ)の組み立て(313~362行目)
いよいよ、時価評価の対象となる金融商品(Instrumentオブジェクト)を作ります。ここでは、シンプルな期間5年の金利スワップを、スポットスタートと、1年後のフォワードスタートの2種類作っています。
(1) 部品を準備
まず、スワップの取引条件を、部品として作成します。
| 看做し元本(314行目) | 1,000,000 ユーロ |
| 固定金利キャッシュフロー (316~321行目) |
|
| 変動金利キャッシュフロー (324~326行目) |
|
| スワップの期間(328) | 5年 |
| スワップタイプ(329) | Payer |
| スワップのエンド日(331) | 決済日(2営業日後)から5年目 |
| 固定金利キャッシュフローの発生日 (332~336行目) |
Scheduleオブジェクトで生成 |
| 変動金利キャッシュフローの発生日 (337~341行目) |
Scheduleオブジェクトで生成 |
| 休日を特定するCalendar(67行目) | TARGET |
以上で部品が揃いましたが、1点だけ注意点。325 行目で変動金利キャッシュフローの指標金利を 6 か月物 Euribor と指定しましたが、そのオブジェクトを生成するコンストラクターに、先ほど作成した forecasting カーブ(変数名 forecastingTermStructure)を渡しています。将来の変動金利キャッシュフローは、このカーブからフォワード金利カーブを導出して求めます。
(2) Instrument(VanillaSwapオブジェクト)の生成
部品が揃ったので、いよいよ Instrument を組み立てます。まず一つめの商品としてスポットスタートの5年金利スワップ(VanillaSwapオブジェクト)を作成します(342~345)が、コードを見ての通り、部品をコンストラクターに渡してオブジェクトを作成するだけです。
次に、1年後スタートで、期間5年のフォワード金利スワップを作成します。347、348 行目でスタート日を 1 年後に設定すれば、後は同じで VanillaSwap のコンストラクターに部品を渡して、オブジェクトを作成するだけです。
これで2つのInstrumentが完成しました。
1.2.3.4.5. PricingEngineの組み立て、価格の計算、画面出力(391~508行目)
最後に、PricingEngine を組み立て、それを上記の Instrument オブジェクトに設定すれば、価格計算が行えます。シンプルな金利スワップ(VanillaSwapオブジェクト)の価格エンジンはDiscountingSwapEngineクラスを使います。この価格エンジンの部品は、既に作成済みの OISカーブ(変数名discountingTermStructure)だけです。
コードの大半は、画面出力用であり、PricingEngineの作成、Instrument オブジェクトに設定、価格計算の部分は、下記の通りわずかです。
(1) スポットスタートの5年物スワップの価格計算(406~413行目)
- PricingEngineの作成(406)
- VanillaSwapオブジェクトへ設定(408)
- 価格計算(411~413)
(2) フォワードスタートの5年物スワップ()
- PricingEngineの作成(406)
- VanillaSwapオブジェクトへ設定(409)
- 価格計算(434~436)
PricingEngineは、価格計算以外にも、いくつかの計算アルゴリズムを備えています。このプログラム例にもある通り、
- Fair Spread の計算 : 現在の市場金利を基準にした場合、特定の固定金利のスワップを取り組んだ場合に、変動金利に加算(あるいは減算)するスプレッドは何%が適切なのか
- Fair
Rate の計算 : 現在の市場金利を基準にした場合、スプレッド0の変動金利キャッシュフローに対し、何%の固定金利のスワップが適切なのか
の計算機能があります。それ以外にも
- basis point sensitivity
- オプションの Greeks(リスク感応度)
などのリスク量の計算機能もあります。いずれも価格計算のアルゴリズムを、応用して導出します。
以上が、MulticurveBootstrappingプロジェクトの内容でした。
1.2.3.4.6. Appendix
Appendix-1 Quote クラス
Quateクラスは、市場データを格納する為のクラスです。QuantLibでは、Quoteクラスをベースクラスとし、市場データの種類に合わせて、いくつかの派生クラスを定義しています。その基本的な役割は、データの保持と、そのデータへのアクセス用関数の提供です。Reference Manualから、Quoteクラスから派生する様子を示した図を抜き出しました。
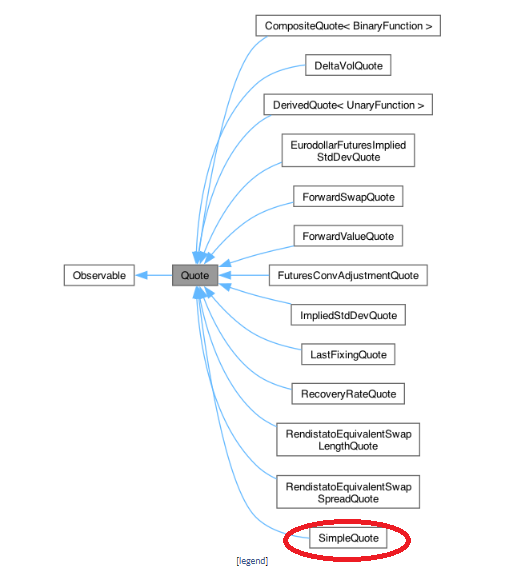
この図にある通り、プログラム例で使われているSimpleQuoteは、Quoteの派生クラスです。Quoteされているデータのタイプ(価格なのか、金利なのか、Volatilityなのかなど)によってバリエーションが発生しています。そして、QuoteクラスのベースクラスはObservableと呼ばれるクラスです。
Quote クラスそのものの役割はシンプルで、詳細な解説は不要かと思います。一方、そのベースクラスとなる Observable クラスとしての役割は、はるかに重要で、その機能は複雑です。Observable クラスと、それと対をなす Observer クラスは、デザインパターンのひとつである、Observer パターンを使って設計されています。実は、これまで解説してきた Instrument クラスや PricingEngine クラスや TermStructure クラスも、すべて Observer あるいは Observable、あるいはその両方の派生クラスとして定義されています。
そこで、Quoteクラスの解説はそこそこにし、以下にObserverパターンについて解説したいと思います。
Appendix-2 Observerパターンについて
金融商品の価格計算は、あたりまえですが、必ず市場データを使います。実務では、それを Reuter や Bloomberg や、あるいは証券取引所といった市場データの提供会社から電子データとして取得します。もし実践で QuantLib を使うのであれば、外部データと接続用の API を使い、QuantLibライブラリに取り込む事になるでしょう。QuantLibは、それをObservableクラスの派生クラスであるQuoteクラスのオブジェクトに格納する事になります。
ここでひとつ大きな問題が発生します。すなわち
― 常に変動する市場データに対し、どう対応するか?
という事です。
市場データは、絶えず変動しているので、それによってデリバティブズ商品の価格も変動します。QuantLib の中心的なクラスとなる Instrument と PricingEngine も、当然市場データに依存するので、市場データが変化したかどうかを監視する必要があります。データが動けば、価格計算をやり直す必要があるからです。そこで、そのような監視機能を、Observer クラスにまとめ、市場データに依存するオブジェクトはすべて、その派生クラスとして定義します。
一方、市場データを保持する Quote クラスは、監視される側(Observableクラス)になります。この Observable クラスは、自分を監視しているすべての Observer を、登録(register)しています。具体的には、自分を監視している Observer のポインタをメンバー変数として保持しています。そして、Observable のデータが更新された場合、そこに登録しているすべての Observer に対し、その事を通知します。通知を受け取った Observer 側は、データが変更された旨のフラッグを立て、価格の再計算に備えます(直ちに価格の再計算をする訳ではありません)。
この関係を図示すると、次の様になります。
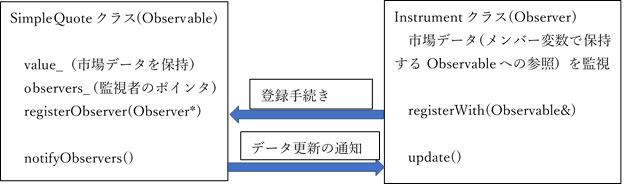
これが、Observerパターンの最も基本的な役割です。
このプログラム例で示されている、イールドカーブ構築から Instrument と PricingEngine オブジェクトの生成においては、Observer と Observable の関係が、多重的になっています。すなわち、市場データを保持している SimpleQuote オブジェクトが、そのまま Instrument と PricingEngineの部品になる訳ではありません。
SimpleQuote オブジェクトは、まず Handle に格納され、それが BootstrapHelper オブジェクト(下記の図では RateHelper となっていますが同じものです)の中に取り込まれます。BootstrapHelper が Observerで(Handleを経由して) SimpleQuote が Observable となる関係が出来上がります。
そして、BootstrapHelper は、YieldTermStructure の部品になります。今度は、BootstrapHelper が Observable の役割になり、YieldTermStructure が Observer となります。
最終的にYieldTermStructureオブジェクトが、Instrument と PricingEngine の部品としてそれぞれのオブジェクトに取り込まれますが、その結果 YieldTermStructure が Observable となり、Instrument と PricingEngine が Observer となります。
以上を図示すると下記のような関係です。
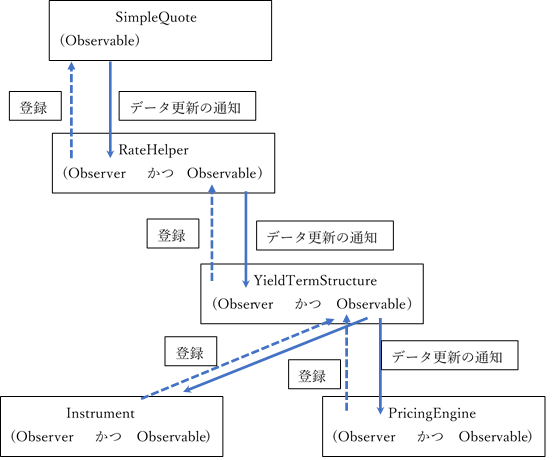
Instrument と PricingEngine も Observable の役割を持っており、この商品や価格エンジンのデータに依存する他の Observer オブジェクトから監視される側になる事も想定されています。
Observable を部品として、Observer オブジェクトを組み立てると、そのコンストラクターを起動する際に、上記の登録の手続きが自動的に行われます。MulticurveBootstrapping プロジェクトのプログラム例では、
- SimpleQuoteを使って、Handleオブジェクトを生成
- そのHandleオブジェクトを使ってBootstrapHelperオブジェクトを生成
- BootstrapHelper オブジェクトを使って、YieldTermStructure オブジェクトを生成
- YieldTermStructureオブジェクトを使って、InstrumentとPricingEngineを生成
する際に、それが行われています。
デザインパターンである Observerパターンについては、Luigi Ballabio氏の“Implementing QuantLib : Odds and ends : Observer Pattern”に詳細な解説があり、それを参考にして下さい。その部分の日本語訳はこちら
Appendix-3 Handle<TemplateClass>クラス
先ほど説明した Quote オブジェクトは、市場データを保持しますが、それを BootstrapHelper や PricingEngine などの部品として使う場合、Quote オブジェクトのポインタを渡すのではなく、そのポインタのポインタを使います。その仕組みは、QuantLib が用意した Handle<TemplateClass>クラスで提供されています。
プログラム例にある通り(118行目など)、BootstrapHelper を作成している for ループの中で、Quote オブジェクトのポインタを使って、一旦 Handle<Quote>オブジェクトを作成し、それを BootstrapHelper のコンストラクターに渡しています。Handle<Quote>オブジェクト自体がポインタとして生成されるので、Handleはポインタのポインタになります。
Handle<TemplateClass> の内部構造は、若干複雑で、その仕組みは Luigi Ballabio氏の "Implementing QuantLib : SmartPointers and Handles"に解説があるので、そちらをご覧ください。(その日本語訳はこちら)
ここでは、市場データを部品として、より大きな部品に組み込む場合、なぜポインタのポインタである Handle クラスを使うのかについて、若干の説明をします。
市場データのデータソースは、通常、複数存在します(取引所、Reuter、Bloomberg、ブローカーなど)。すると、PricingEngine や TermStructure など、市場データに依存するオブジェクトは、市場データをスイッチできる仕組みが必要になります。その場合、各オブジェクトが Quote オブジェクトのポインタを直接保持すると、データソースの変更があった場合、それに依存しているすべてのオブジェクトで、データソース入れ替え操作が必要になります。
そこで、Handle オブジェクトに、Quote オブジェクトのポインタを持たせ、その Quote に依存するオブジェクトは、すべてその Handle を保持するようにします。すると、データソースのスイッチは、Handleが保持するQuoteのポインタを変更する 1 回の操作だけで、Handle に依存するすべてのオブジェクトで、データソースの取り換えが可能になります。これが、ポインタのポインタを使う理由です。
Handle のもうひとつの役割は、Observer―Observable の依存関係を、Handle を経由しても行える点です。その仕組みは、若干複雑で先ほどの Luigi Ballabio 氏の文献を参照して下さい。
Appendix-4. BootstrapHelper< YieldTermStructure> (別名 RateHelperクラス)
このクラスは、YieldTermStructure クラスをテンプレート引数に取る、クラステンプレートです。
ところで、MulticurveBootstrapping プロジェクトのソースコードに、BootstrapHelper<YieldTermStructure>の名前は見当りません。その代わり 90 行目(下記に抜き出し)を始め、RateHelper というクラス名がいたる所で使われています。
90行目: std::vector<ext::shared_ptr<RateHelper>> eoniaInstruments;
RateHelper クラスは、BootstrapHelper<YieldTermStructure>クラスから typedef を使って宣言されたクラスであり、要は別名です。BootstrapHelper<YieldTermStructure>というクラス名が長すぎるので、簡略化した呼び名を付けたようです。BootstrapHelper という名前の方が、実際にこのクラスが果たす役割にマッチしているので、以下はその名前を使って解説します。
本文中で説明した通り、BootstrapHelper の役割は、期間(pillar)ごとのベンチマーク商品のキャッシュフローと市場価格から、Discount Factor を未知数とする方程式を提供するものです(同時に、Pillar を特定する役割もあります)。プログラム例では、そのベンチマーク商品の種類に合わせ、それぞれに対応する派生クラスが使われています。下の図は、Reference Manual から抜粋した、BootstrapHelper の派生クラスを示すダイアグラムです。様々な商品がカーブ構築の際のベンチマーク商品になり得るので、それぞれの商品に対応するクラスが用意されています。その中で、楕円で囲まれたクラスが、このプログラム例で使われたBootstrapHelperの派生クラスです。
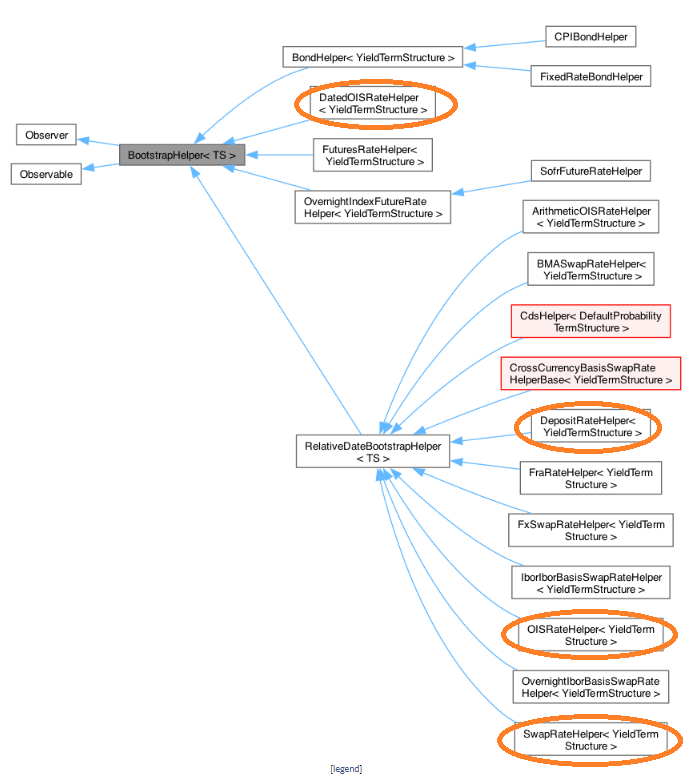
上のダイアグラムにある通り、BootstrapHelperは、BootstrapHelper<YieldTermStructure>という名前のClass Templateで、テンプレート引数には、YieldTermStructureクラス(の派生クラス)が入ります。このテンプレート引数で与えられたイールドカーブから Discount Factor を抜き出し、Pillar ごとの商品の市場価値を計算します。それが市場価格と一致するような方程式を提供します。
ちなみに、BootstrapHelper は、Observer と Observable クラスの派生クラスであり、BootstrapHelper が取り込む Quoteオブジェクトに対する Observer となり、BootstrapHelper オブジェクトを取り込む YieldTermStructure の Observable になります。
Appendix-5. PiecewiseYieldCurve<Discount, Cubic,…>クラス
このテンプレートクラスは、Boostrapping+Interpolation のアルゴリズムを備え、それを使って YieldTermStructure クラスのオブジェクトを構築するクラスです。クラスの構造や、アルゴリズムの実装方法は非常に複雑で、その解説は控えます。詳しく知りたい方は、以下の情報を参考にして下さい。
Boostrapping + Interpolation 法のアルゴリズムについては
PiecewiseYieldCurve<...>の構造と使用例については
このクラスの構造を見る為に、PiecewiseYieldCurve<...>クラスを定義しているヘッダーファイルを見てみます。(piecewiseyieldcurve.hpp にあります。QuantLib ライブラリのソースコードから探してみて下さい)
template <class Traits, class Interpolator,
template <class> class Bootstrap = IterativeBootstrap>
class PiecewiseYieldCurve
: public Traits::template curve<Interpolator>::type,
public LazyObject {…
ここから分かる通り、このクラスは、下記の3種類のテンプレート引数を持つ、テンプレートクラスになります。
| Class Traits |
| Class Interpolator |
| Template <class> class Bootstrap=IterativeBootstrap |
1つ目のテンプレート引数はTraitsとなっていますが、ここではInterpolationの対象となるYieldTermStructure<Interpolator>の派生クラスを指定します。直接そのクラス名を指定するのではなく、Traitsを使って間接的に指定します(なぜそうするかの説明は、Implementing QuantLibの解説を参照して下さい)。Traitsは(私がソースコードの中から見つけた限り)以下の4種類用意され、それぞれYieldTermStructureクラスの派生クラスを特定しています。(bootstraptraits.hppファイル参照)
| Discount | : InterpolatedDiscountCurve <Interpolator> |
| ZeroYield | : InterpolatedZeroCurve<Interpolator> |
| ForwardRate | : InterpolatedForwardCurve<Interpolator> |
| SimpleZeroYield | : InterpolatedSimpleZeroCurve<Interpolator> |
それぞれ、どのようなカーブかは、クラス名から自明でしょう。但し、クラステンプレートである Interpolator の部分は、次の 2 番名のテンプレート引数で特定されます。
2つ目のテンプレート引数は Interpolator (これもClass traitsです)となっていますが、QuantLib が用意している様々な Interpolation Class の中から、Interpolationの方法を指定します。代表的なのは
| Cubic |
| LogLinear |
| Linear |
3つめのテンプレート引数は、Bootstrapping + Interpolation アルゴリズムの中で、連立方程式を解くアルゴリズムです。デフォールトで IterativeBootstrap が指定されています。これは、Solver を使って方程式を解くアルゴリズムになります。実務では、殆どこの方法を使っているので、デフォールト設定されたと思われます。 従って、プログラム例の中で PiecewiseYieldCurve<Traits, Interpolator, Bootstrap>のインスタンスを生成した際に、3番目のテンプレート引数は、省略されていました。
上記の通り、この3種類のテンプレート引数で、Interpolation の対象となるイールドカーブの種類、Interpolation の方法、Bootstrap の方法、を指定した事になります。この例では、① Discount Curve を、② Cubic Spline 法によるInterpolation を行いながら、③ Solver を使った方程式の解を求めるアルゴリズムで、構築している事になります。
まだ疑問が残ります。Cubic Spline による Interpolation 法は、多くのバリエーションがあります。テンプレート引数で Cubic と指定していますが、どの Cubic Spline 法が不明です。これも、Cubic のデフォールト設定により、内容が特定されています。ここでは、その詳細の説明は省略しますが、数々の Cubic Spline 法の定義内容は、ソースファイルの cubicspline.hpp に書かれているので、そこで確認して下さい。
要は、非常に複雑で、様々な選択肢がある Boostrapping + Interpolation 法のアルゴリズムの中から、とりあえず QuantLib が用意した方法を使えば、イールドカーブが簡単に作成できるという事です。
<ライセンス表示>
QuantLibのソースコードを使う場合は、ライセンス表示とDisclaimerの表示が義務付けられているので、添付します。 ライセンス