1. QuantLibを使ってみる
1.2 テストプログラムを試す
1.2.2 EquityOption プロジェクト : シンプルな株式オプションの価格計算 (続き)
1.2.2.4 ソースコードの解析
1.2.2.4.1 部品の作成
まず、Instrument オブジェクトと PricingEngine オブジェクトの部品の生成から
| (1) | 日付のデータ(52~56行目) | ||||||||||||||
| "カレンダー"、"本日"、 "決済日(取引のスタート日)"、 "時価評価日" といった日付データが、部品の原料として提供され、それを使ってCalendar, やDate型のオブジェクトを生成しています。CalendarやDateはQunatLib内で定義されたクラスです。それぞれのクラスの意味は Appendix :Date Calendar DayCount クラスについて を参照。 ちなみに、Calendar オブジェクトとして設定されている TARGET は、欧州中銀の資金決済システムがオープンしている営業日を示すカレンダーです。 |
|||||||||||||||
| (2) | オプションの取引条件と市場データ(58~66行目) | ||||||||||||||
オプション価格の計算に必要な取引条件と、市場データが、部品の原料として提供され、それらを使って部品の部品が生成されています。
|
(それぞれの変数の型宣言として、Real、Spread、Rate、Volatility、という、QuantLib内で定義された型で宣言されていますが、いずれもdouble型を示します。こうする事で、宣言された変数の意味が明快になります。それぞれの意味についてはAppendix:Numeric Types)
| (3) | (1)と(2)の画面出力(68~88行目) : 上記の情報をコンソール画面に出力しています。 |
| (4) | Exerciseオブジェクト(90~98行目) |
オプション行使日の情報を原料にして、Exercise クラス(その派生クラスであるEuropeanExercie、BermudanExercise、AmericanExercise)のオブジェクトを生成しています。コードは以下の通りです。(注:ext:: は、boostからc++11へ移行する際に、互換性を残すために QuantLib 内で特別に作られた namespace で、環境設定(boostを使うか否か)に従って、 boost と std のスイッチが行われます。 その説明は Appendix:ext:: namespace ) |
| (5) | リスクフリー金利、配当、Volatilityのカーブ(102~109行目) |
| それぞれ、(1) (2) で生成した部品を使って、TermStructureクラス(の派生クラス)のオブジェクトを生成ししています。TermStructure クラスは QuantLib 内で、最も重要なクラスのひとつですが、これについては、別の Example の所で詳しく解説する予定なのでここでの説明は飛ばします。 また、Handle<T>は、T 型のオブジェクトに対するポインターのポインターになりますが、これについても、別の Example の解説の時に説明します | |
| (6) | Payoffオブジェクト(110行目) |
| (2)で用意されたオプションタイプ(ここではPut)と、ストライク価格(strike=40)を使って、Payoff クラス(の派生クラスである PlainVanilaPayoff クラス)のオブジェクトを生成。 | |
| (7) | 確率過程オブジェクト(111~112行目) |
StochasticProcessクラスの派生クラスであるBlackScholesMertonProcessクラスのオブジェクトを、上記ですでに生成済みの下記部品を使って組み立てています。
|
ここで生成された、Black Scholes Merton 過程(=モデル)は、Black Scholes モデルを拡張して、対象資産(株や外国為替)に配当あるいは金利が発生する商品に対応したモデルです。
1.2.2.4.2 Instrument オブジェクトと PricingEngine オブジェクトの組み立て
以上で、Instrument と PricingEngine の部品生成が終わりました。これらを使って、Instrument オブジェクトと PricingEngine オブジェクトを組み立て、PricingEngine オブジェクトを Instrument オブジェクトに設定(メンバー変数として登録)します。
(1) Instrumentオブジェクト(114~117行目):上記の(4)と(6)で生成された Exerciseオブジェクトと Payoffオブジェクトを部品とし、3種類の VanillaOptionクラス(Instrumentの派生クラス)のオブジェクトを組み立てています。以下のコードは、その組み立ての様子です。部品から組み立てるというと大変そうに聞こえますがが、部品をコンストラクターに渡しているだけで、これで完成です。
VanillaOption europeanOption(payoff, europeanExercise);
VanillaOption bermudanOption(payoff, bermudanExercise);
VanillaOption americanOption(payoff, americanExercise);
(注:VanillaOptionクラスは、Optionクラスの派生クラスで、OptionクラスはさらにInstrumentクラスの派生クラスです。その継承関係は Appendix: VanillaOption クラス )
(2) PricingEngine オブジェクトの生成と、Instrument オブジェクトへの設定(123行目):
この1行(下記に抽出)で、PricingEngineの組み立てと、それをInstrumentオブジェクトに設定するのを同時に行っています。
europeanOption.setPricingEngine(ext::make_shared(bsmProcess));
このコードは、VanillaOption オブジェクト(変数名europeanOption)のメンバー関数である setPricingEngine(…) を呼び出しています。この関数は、PricingEngine オブジェクトを Instrument オブジェクトに設定する(メンバー変数に取り込む)関数です。
ところが、その PricingEngine オブジェクトは、この段階では未だ出来ていません。そこで、上記のコードにある通り、PricingEngine クラスのコンストラクターを引数として、setPricingEngine(…)へ渡して、この関数呼び出しと同時に PricingEngine オブジェクトが生成されています。ここでは、AnalyticEuropeanEngine クラスのオブジェクトが生成されており、その部品には、先ほど生成した bsmProcess(BlackScholesMertonProcessオブジェクト)が使われています。もうひとつの重要な部品であるTermStructureオブジェクトは、bsmProcess を生成する時にその部品となって、間接的にPricingEngineに取り込まれています。
部品の生成には行数がかかりましたが、InstrumentオブジェクトとPricingEngineオブジェクトの組み立ては、それぞれたった1行です。
1.2.2.4.3 価格計算の実行と画面出力
価格計算とコンソール画面出力(121~129行目):ここでは、ヨーロピアンオプションの価格を Black Scholes Merton のオプション価格式(解析解)を使って計算し、それをコンソール画面に出力しています。価格計算は 126行目にある europeanOption.NPV() 関数の呼び出しで実行されました。
コンソール画面出力のBlack-Scholesの行がそれです。
1.2.2.4.4 その他のPricingEngineオブジェクトの組み立てと価格計算
131行目以降は、その他の20個の価格エンジンの組み立てと、価格計算、その画面出力を行っています。それぞれの価格エンジンは、使われるオプションモデルの違いと、使われる価格計算アルゴリズムの違いで、使われる部品にバリエーションが発生します。
ここでは、それぞれの価格エンジンが、どのような部品から組み立てられているかの説明に留め、オプションモデルの内容や、数値解のアルゴリズムの説明は行いません。
| (1) | Black Scholes Merton モデル |
| 価格エンジンの組み立てについては既に説明しました。 | |
| (2) | Black Scholes Merton + Vasicekモデル(131~146行目) |
| 株と金利が確率変数となる2ファクターモデルになります。価格エンジンはAnalyticBlackVasicekEngineが使われており、その部品は、(1).Vasicekモデルのオブジェクト、(2)既に生成したBlackScholesMertonProcessのオブジェクト、さらに、(3)株と金利の相関係数、になります(140行目の.setPricingEngineに渡されたコンストラクター参照)。143行目でNPV()メソッドで価格計算を行い、画面出力しています。/td> |
| (3) | (semi-analytic) Hestonモデル(148~160行目) |
| Hestonモデルは、Stochastic Volatilityモデルの一種です。ここで使われている価格エンジン(AnalyticHestonEngine)は、Hestonが導出した解析的近似解で価格を計算します。 この価格エンジン(及び、次のBatesモデルの価格エンジン)の部品構成は、他の価格エンジンと若干異なります。 1 まず、Hestonモデルで使われているパラメータをコンストラクターに与えて、HetonProcessオブジェクトを生成しています。 2 次に。これを部品として、HestonModelクラスのオブジェクトを組み立てています。 3 最後に、そのHestonModelオブジェクトを使って価格エンジンの部品として使うようになっています。 上の2の部分が他のPricingEngineの部品には無い部分です。理由は、Hestonモデルを使う場合、モデルパラメータのCalibrationが必要になります。このHestonModelオブジェクトの中に、そのアルゴリズムが実装されています。 |
|
| (4) | ④ (semi-analytic)Batesモデル(162~175行目) |
| Batesモデルは、Heston モデルにJump Diffusionのファクターを加えたものです。価格エンジンは、まずBates過程を記述する BatesProcessオブジェクトを作り、それを使ってCalibration用の BatesModelオブジェクトを生成し、さらにそれを使って、BatesEngineを組み立てています。 |
Heston モデルも Batesモデルも、モデルパラメータの Calibration が必要ですが、その為にはベンチマーク商品の価格(ストライク価格軸のImplied Black Volatilityカーブ)データが必要です。ただこのExampleでは、そのデータを用意していません。計算結果は、Black Scholes Mertonモデルの結果とほぼ一致しているので、結局、テスト用オプション取引にだけCalibrationされた結果だと思います。
5 から 9 までのモデルは、アメリカンオプションの価格を、解析的近似解で求める価格エンジンです。このテクニックは、昔からありましたが、価格に若干の下方バイアスがかかる欠点があり、あまり使われていなかったのではないかと思います。ところが、7, 8, 9, の QD+ (参考文献を見ると2015年頃に発表されたようです。私も最近になるまで知りませんでした)の計算結果をみると(コンソール出力画面参照)、数値解とそん色ない計算結果になっています。であれば、数値解よりは計算速度が速いので使えそうです。いずれの価格エンジンも、部品は、既に作成済みのBlackScholesMertonProcessオブジェクト(変数名bsmProcess)のみであり、価格エンジンの組み立ても簡単です。モデルの中身(アルゴリズム)などの詳細な説明は飛ばします。
| (5) | Barone, Adesi, Whaley のアメリカンオプション用の近似解アルゴリズム(177~185行目) |
| (6) | Bjerksund and Stenslandのアメリカンオプション用の近似解アルゴリズム(187~195行目) |
| (7) | QD+ fixed point (高速) (198~205行目) |
| (8) | QD+ fixed point (精確) (198~205行目) |
| (9) | s QD+ fixed point(高精度) (198~205行目) |
10~21までは、数値解のアルゴリズムを使った価格エンジンによるものです。
| (10) | 数値積分法(228~236行目) |
| 数値積分法による価格計算を行っています。価格エンジンとしてIntegralEngineクラスのオブジェクトを使って価格計算をしています。部品は BlackScholesMerton 過程のみです。数値積分法も、シンプルな台形則から、複雑なガウス求積法など、いくつか存在しますが、このエンジンの内部でどのアルゴリズムが走っているかは、調べていません。興味がある方は、ご自分でソースコードを確認して下さい。 |
次に、有限差分法を使った価格エンジンです。有限差分法は、アメリカンオプションやバリエーションオプションの価格計算の為に、実務でもよく使われるテクニックです。
| (11) | 有限差分法(238~253行目) |
| 価格エンジンは、FdBlackScholesVanillaEngine クラスのオブジェクトで、部品は BlackScholesMertonProcess オブジェクトに加え、時間軸と状態変数軸の両方のステップ数が必要です。後者については 239行目で 801という値が与えられています。 |
次の 7 種類の価格エンジンは、すべて 2項ツリーのバリエーションになります。価格エンジンの部品は、既に生成済の BlackScholesMertonProcess(変数名bsmProcess)と時間ステップ数(変数名timeSteps)です。なので、価格エンジンの組み立てはコードにある通り、シンプルです。実務では、アメリカンオプションやバーミューダンオプションの価格評価に、2項モデルよりも先ほど述べた有限差分法を使う方が多いと思います。なので、各モデルの解説は飛ばします。
| (12) | Jarrow-Rudd二項モデル(255~266行目) |
| (13) | Cox-Ross-Rubinstein二項モデル(268~279行目) |
| (14) | 同確率二項分岐モデル(281~292行目) |
| (15) | Trigeorgis 二項モデル(294~305行目) |
| (16) | Tian二項モデル(307~318行目) |
| (17) | Leisen-Reimer二項モデル(320~331行目) |
| (18) | Joshi二項モデル(333~344行目) |
次の 3 種類の価格エンジンは、モンテカルロシミュレーション(以下MCS)を使ったエンジンです。本来なら、非常に複雑で多様なバリエーションがあるアルゴリズムですが、この例の通り、極めてシンプルに価格エンジンが作られています。
| (19) | モンテカルロ法―疑似乱数(346~361行目) |
| 疑似乱数(Pseudo Random)を使ったシミュレーションを行います。価格エンジンはMakeMCEuropeanEngine<PseudoRandom> | |
| (20) | モンテカルロ法―Sobol列(363~376行目) |
| 低乖離数列(Low discrepancy sequence準乱数 Quasi Randomとも呼ばれています)の中からSobol列を使ったシミュレーション。価格エンジンはMakeMCEuropeanEngine<Sobol> | |
| (21) | モンテカルロ法―Longstaff-Schwartz最小2乗法(378~392行目) |
| 最小2乗法を使って、モンテカルロシミュレーションでアメリカンオプションの価格計算を行うアルゴリズムです。価格エンジンに、いくつかのパラメータを部品として与えていますが、その意味や、Longstaff-Schwartzの手法については、上級編のMCSの解説:Least Squares Monte-Carloの中で簡単に説明しています。 |
MCS のアルゴリズムは、様々なバリエーションがあります。例えば、一様乱数発生方法、一様乱数から標準正規乱数への変換方法、分散逓減法、などは、いくつかの選択肢があり、どれを使うのがいいか、ケースバイケースで決める必要があります。また、サンプル数をどうするか、離散化バイアスを小さくする為のテクニックなどもあり、本来なら、かなり多数の部品を用意しないと、アルゴリズムが具体化できないはずです。しかし、上記の例の価格エンジンの組み立てには、わずかな数の部品とパラメータしか使っていません。エンジン構築の裏側で、いくつかのデフォールト設定があり、ユーザーが指定しなくても、開発者が選択したオプションで価格エンジンが作られています。それがどのようなものかや、Luigi Ballabio 氏の”Implementing QuantLib”の "Monte-Carlo Framework" のチャプターで解説があるので、そちらを参考にして下さい。
MCS については、その全容の説明には本1冊分かかるので、ここでは行いません。本 Webサイトの上級編で若干の解説をしているので、興味がある方はそちら(上級編 6.6 モンテカルロシミュレーション)を参考にして下さい。
1.2.2.5 まとめ
これまで見てきた通り、このサンプルプログラムでは、3 種類のオプション(Instrumentオブジェクト)を、21 種類の価格エンジン(PricingEngineオブジェクト)を使って価格評価しています。そして、Instrument オブジェクトと PricingEngine オブジェクトは、それぞれ重要部品で作られ、その重要部品は、さらに小さな部品群から作られます。
QunatLib では、債券、スワップ、オプションなどのカテゴリーに含まれるかなりの数の金融商品がクラスライブラリーとして提供されています。また、それぞれについて、複数の価格計算エンジンもクラスライブラリーとして提供されています。しかし、具体的にどの金融商品をどの価格エンジンを使って価格計算するか、さらに、その金融商品と価格エンジンをどういった部品からどのように組み立てるかといった、設計図は存在していません。実際に組み立てるには、金融商品のキャッシュフローやリスク特性、およびその商品の時価評価に使えるモデルが何かが分かってないと、難しいと思います。仮に、それらが分かっていても、QuantLibが用意しているクラスライブラリの中から、どれを選択するか判断しなければなりませんが、そういった場合の判断材料として、以下のような情報にあたれば、ある程度ヒントが得られると思います。
- クラス名 :クラス名から、どういった商品の種類や、価格エンジンの種類・アルゴリズムがある程度推察できます。
- コンストラクター : 商品と価格エンジンが特定できれば、それぞれのコンストラクターを見れば、まず必要な主要部品が分かります。次に、その主要部品のコンストラクターを見れば、さらに小さな部品群が分かります。
- ソースコード : 最終的には、商品や価格エンジンのクラスのソースコードを見れば、そのクラスのオブジェクトが、どのような部品から作られ、どのような計算を行えるか分かります。当然、相当程度の C++ の文法や、商品知識、金融工学の知識が必要になります。
- Examples プロジェクト : 19個のプロジェクトで、そこでカバーされている主要な商品と、それに対応する価格エンジンの組み立て方法が、具体例で分かります。
< Appendix >
・ Dateクラス、Calendarクラス、DayCounterクラス
金融工学に関する理論を、実務のシステムに落とし込む上で、実務家が最初に直面する問題が、日数計算に関する実務上の取り扱いです。私自身、デリバティブズ取引に携り始めた頃、最も頭を悩まされたもののひとつが、日数計算でした。クーポン発生日が休日あるいは月末の場合の取り扱い、うるう年の取り扱い、経過利息計算の際の日数計算方法などは、国や取引市場や商品の種類によって多種多様です。金融商品の価格を計算しようとする場合、こういった実務での取引慣行を正しく反映した計算を行わなければなりません。
QunatLibでは、こういった多種多様な取引慣行に従った日数計算方法を、クラスライブラリーとして提供しています。そのメインになるクラスは以下の3つです。
- Dateクラス
- Calendarクラス
- DayCounterクラスです。
これらのクラスについては、Luigi Ballabio氏のImplementing QuantLibに、解説が載っています その 日本語訳
DayCounterについては、世界中の様々な日数計算ルールが、Wikiで解説されているので、それを参考にして下さい。Day count convention - Wiki 但し、どの金融商品が、どの日数計算方法を使っているかについては、検索エンジンを使って、商品 + 日数計算方法あるいは US Treasury(例) + day count convention などで検索してみて下さい。
・数字の型 (Numeric Types)
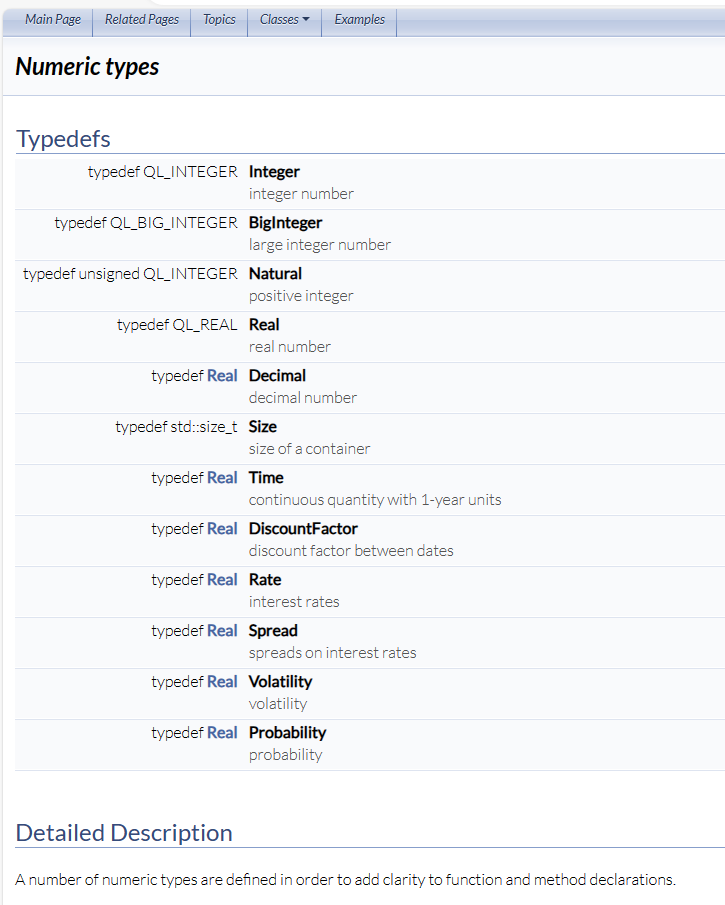
QuantLib では、intとかdoubleといった数字の型を、IntegerとかRealなど独自の型定義で表示しています。変数の型宣言で使われている、RateとかSpreadとかVolatilityはすべてマクロでReal(double)に変換されます。QuantLibが定義している数字の型は、下記のようなものがあります。(QunatLib Reference Manualから抜粋)
何等かの数字を格納する変数について、このような型定義をすれば、変数の意味がより明確になり、読みやすいコードが書けます。
・ auto (自動型宣言)
auto は c++11 から取り入れられた自動型変換機能です。ソースコードの例でみてみます
auto europeanExercise = ext::make_shared< EuropeanExercise > (maturity);このコードでは、europeanExercise という名前の変数を auto で型宣言しています。変数 europeanExercise は、右辺の make_shared< EuropeanExcercise >()で初期化されています。これは、EuropeanExcercise クラスへのスマートポインタのコンストラクターになっており、そのインスタンスで左辺の変数を初期化したことになります。従って、変数 europeanExercise の型は shared_ptr<EuropeanExcercise> でなければなりませんが、その型宣言を auto にすれば、自動的にそう解釈して、その型の変数をメモリ領域に設定してくれます。auto については、Webで様々な解説が検索できるので、それらを参照して下さい。
ext:: namespace について
ext:: は QuantLib が定義した namespace のひとつで、その中で、boost の shared_ptr を使うか、c++11 以降の標準テンプレートライブラリ(std::)に備わった shared_ptr を使うか、切り替え用のマクロが定義されています。
QuantLibは、もともとboostライブラリが提供するスマートポインタを使っていました。ところがc++11以降の規格で、boostの性能に近いスマートポインタが提供されるようになり、QuantLibは、順次stdのスマートポインタへの移行をすすめています。ただ、昔の規格との互換性を持たせるため、環境設定の際に、いずれのスマートポインタを使うか、選択できるようにしています。マクロ設定は、shared_ptr.hpp というヘッダーファイルに書かれているので、そこで内容を確認できます。
StochasticProcess クラス
Option の価格評価に使われる PricingEngine の最も重要な部品のひとつが StochasticProcess クラスのオブジェクトです。Stochastic Process(確率過程)とは、対象資産価格(確率変数)の、微小時間における確率変動の様子を記述した確率偏微分方程式で、一般的に、下の式のような形で表現されます。
\[ dS(t)=μ(…)dt+σ(…)dw(t) \]この式の第1項 \(μ(…)dt\) はドリフト項で時間の変化とともに、確定的(deterministic)に変化する量を示します。第2項 \(σ(…)dw(t)\) は拡散項で、微小な時間でのブラウン運動 \(dw(t)\) による、確率的挙動(Stochastic)での変化量を示します。オプションモデルとは、まさにこの Stochastic Process の事を意味します。モデルのバリエーションは、この式にあるドリフト項係数 \(μ(…)\) と拡散項係数 \(σ(…)\) の関数形(それぞれ定数の場合もあります)のバリエーションや、ブラウン運動の次元の違いによるものです。
QuantLib では、StochasticProcess というベースクラスから、様々なモデルの派生クラスが定義されています。各モデルに対応する派生クラスでは、上式のドリフト項や拡散項の関数形が具体的に記述(メンバー変数として保持)されています。下記に、Reference Manual から抜粋した、StochasticProcess クラスの継承関係のダイアグラムを載せます。
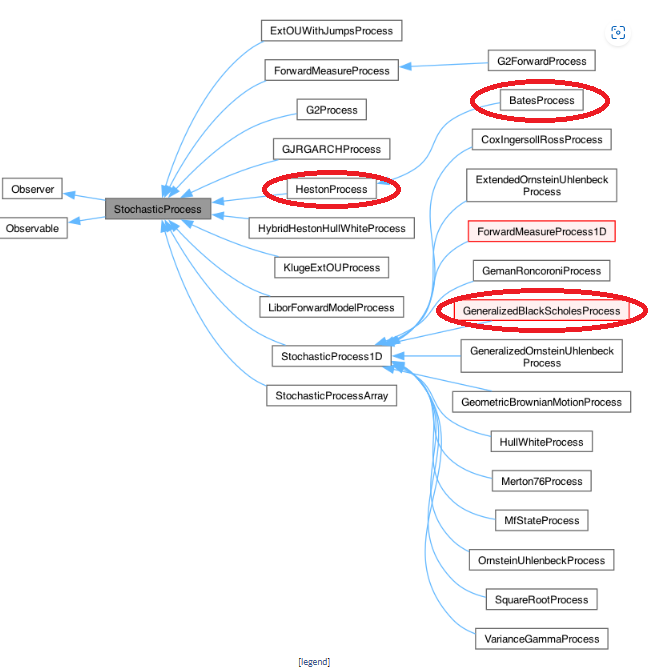
この Example で使われている BlackScholesMertonProcess は、このダイアグラムにある GeneralizedBlackScholesProcess からさらに派生したクラスになります。また同様に Example で使われている HestonProcess や BatesProcess も、このダイアグラムで StochasticProcess クラスから派生している事が分かります。
VanillaOptionクラス
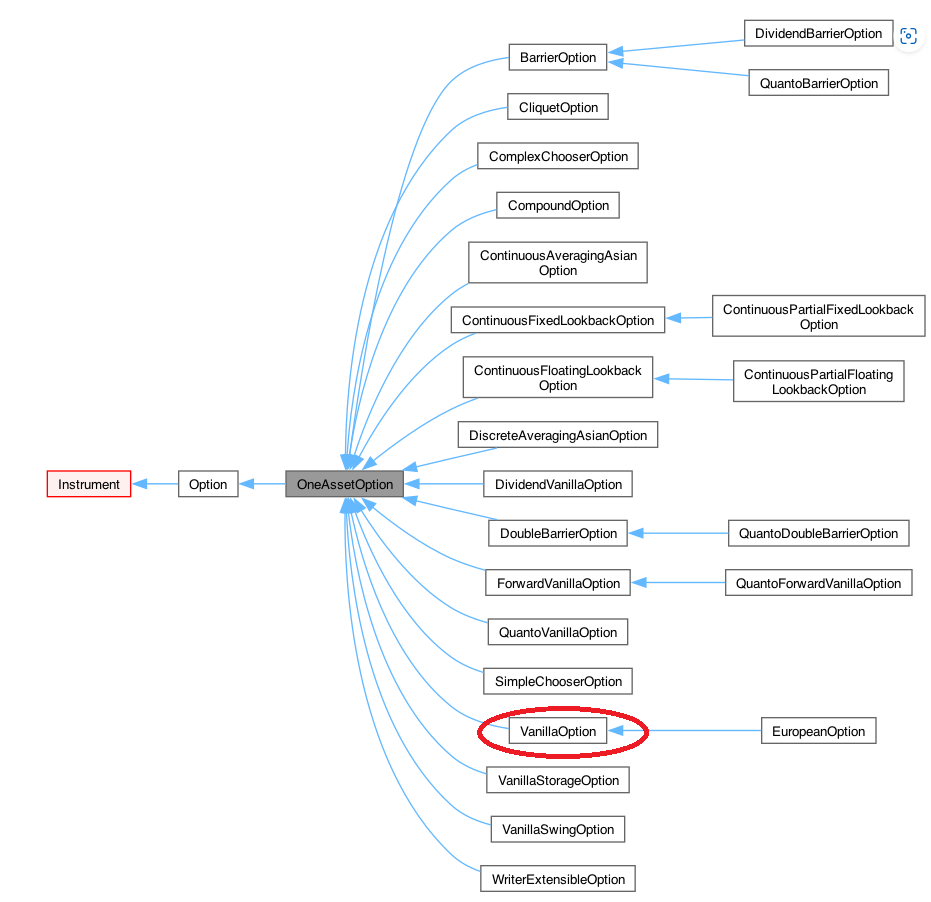
VanillaOptionクラスは、Instrumentクラスから3階層下の派生クラスで、直接の派生元はOneAssetOptionクラスです。Optionクラスの派生クラスのダイアグラムを下に載せますが、QuantLibで提供している様々なオプション商品群が分かります。クラス名から、それぞれどのようなオプション商品か概ね推察できると思います。
<ライセンス表示>
QuantLibのソースコードを使う場合は、ライセンス表示とDisclaimerの表示が義務付けられているので、添付します。 ライセンス