1. QuantLibを使ってみる
1.2 テストプログラムを試す
1.2.4 Bonds プロジェクト (続き)
1.2.4.4 ソースコードの解析
では、ソースコードの中身を詳細にみていきます。前回のプロジェクト同様、イールドカーブの構築にコードの半分以上を使っています。その部分については、前回解説済なので、簡単に済ませ、3種類の債券オブジェクトの構築方法を中心に解説します。またその重要な部品については、Appendix で詳しく解説します。
1.2.4.4.1 時価評価基準日の設定(59~76行目)
まず時価評価日など、日付に関する情報を、下記のように設定します。
| 行番号 | |
| 59 | Calendar calendar = TARGET(); : 使用されるカレンダーをTARGETに設定 |
| 61 | Date settlementDate(18, September, 2008); : 債券の決済日 |
| 63 | settlementDate=calendar.adjust(settlementDate); :上記日付が仮に休日の場合、翌営業日に修正 |
| 65 | Integer fixingDays = 3; :LIBOR金利決定日からスタート日までの日数 |
| 66 | Natural settlementDays = 3; :本日から決済日までの日数 |
| 68 | Date todaysDate = calendar.advance(settlementDate, -fixingDays, Days); : 本日 |
| 70 | Settings::instance().evaluationDate() = todaysDate; : 時価評価基準日 |
ここで指定している fixingDays や settlementDays の数字は、実際の取引慣行と異なっていますが、あくまでテストなので気にしないでいいでしょう。債券の時価評価基準日 evaluationDate は、実務慣行では決済日を基準にしますが、ここではそれを本日にしているので注意して下さい。
1.2.4.4.2 2種類のイールドカーブの構築 (93~360行目)
(1)債券イールドカーブの構築 (93~220行目)
このプロジェクトでもイールドカーブを、キャッシュフローのディスカウント用と、将来の変動金利の予想用、の2種類作成します。まずディスカウント用として、93 行目から220 行目を使って、債券イールドカーブを構築しています。
イールドカーブの構築方法は、MulticurveBootstrapping プロジェクトで既に説明していますので、ここではそれとの違いのみを説明します。イールドカーブの生成アルゴリズム(Bootstrapping + Interpolation法)については、既に説明済ですが、重要なので、再記します。
- 指標金利の観測点となる期間(pillar)を満期とするベンチマーク商品を特定し、その市場レートを取得する。
- そのベンチマーク商品のキャッシュフローから、Discount Factor を未知数とする、次のような方程式を立てる。 \[ Σ ~~商品のキャッシュフロー_i ~~×~~Discount Factor_i~~ =~~商品の市場価格 \]
- 2. の方程式をすべての期間(pillar)で設定し、それを連立させ、
- その連立多元方程式を解く形で、未知数となる Discount Factorベクトルを求める事になります。(詳しくは基礎編:イールドカーブの構築方法(2))
このアルゴリズムに従い、
- まず pillar ごとのベンチマーク商品の市場レート(価格)を取得
93~99行目 : 3か月、6か月、1年の pillar 用の Deposit
120~164行目 : 2,3,5,10,30年の pillar 用の債券
- 次に、pillar ごとに BootstrapHelper オブジェクトを生成する。(BootstrapHelperクラスについては、前回ここで解説済み)
101~117行目 : DepositRateHelper オブジェクトを生成
167~195行目 : FixedRateBondHelper オブジェクトを生成
- 207~217 行目で、2. の BootstrapHelper オブジェクトの配列を生成する(連立方程式にする)。
- 219 行目で、その配列を使って、PiecewiseYieldCurve<Discount,LogLinear> オブジェクトを生成する。すると生成と同時に、連立方程式を解くアルゴリズムが走り、イールドカーブが完成する。
実務では債券イールドカーブを構築する際に、1.のベンチマーク商品は発行体が同じ(同じクレジットリスクを持つ)債券を使わなければなりません。しかし、プログラム例では、3か月、6か月、1年満期の 預金金利 を、ゼロクーポン債と看做して使っています。実際にはあり得ませんが、あくまでテスト用なので目をつぶりましょう。
従って、2. の役割を担う BootstrapHelper は、預金用の DepositRateHelper クラスと、債券用の FixedRateBondHelper クラスのオブジェクトを使っています。174 行目にある、FixedRateBondHelper のコンストラクターをよく見てください。引数として渡している部品は、債券のキャッシュフローを生成するのに必要な情報になっています。これは BootstrapHelper が、ベンチマーク商品の価格計算をする必要上、商品オブジェクトの情報を必要とするからです。この BootstrapHelper は Instrument と PricingEngineを合体させたようなクラスといえます。
(2)変動金利インデックスカーブの構築 (203~360行目)
次に、変動金利債のクーポンキャッシュフローを予測する為に、インデックスカーブを構築します。構築の手順は、前の MulticurveBootstrapping の例で説明したのと同じなので、省略します。
最後に、上記で生成された2種類のイールドカーブを保持するHandleとしてRelinkableHandleオブジェクトを2つ生成しています(364と366行目)。
364 RelinkableHandle<YieldTermStructure> discountingTermStructure;
366 RelinkableHandle<YieldTermStructure> forecastingTermStructure;
この時点では、生成された RelinkableHandle オブジェクトは空ですが、後で460行目と461行目で、既に生成済みの2種類のイールドカーブをリンクさせる事で(そのポインターを取得する事で)、実際のイールドカーブを指し示すオブジェクトの実体が出来上がります。
460 forecastingTermStructure.linkTo(depoSwapTermStructure);
461 discountingTermStructure.linkTo(bondDiscountingTermStructure);
Handleクラスについては、前のセクションで説明済です(Jissenhen1.2.3.4.6 Appendix-3 )。
1.2.4.4.3 Pricing Engine の構築
376 行目で PricingEngine を構築しています。部品は、先ほど生成した債券イールドカーブ(変数名 discountingTermStructure)です。
auto bondEngine= ext::make_shared<DiscountingBondEngine>(discountingTermStructure);価格エンジンの組み立てはこれで終わりです。
1.2.4.4.4 Instrumentオブジェクト(債券オブジェクト)の構築(378~457行目)
次に、価格計算の対象となる債券オブジェクトを3種類(ゼロクーポン債、固定金利債、変動金利債)生成します。
(1) ゼロクーポン債(379~388行目)
ゼロクーポン債は、最もシンプルなキャッシュフローなので、以下のように少数の部品をコンストラクターに渡すだけで完成です。(379 行目)
| settlementDays, | : 取引日から決済日までの営業日数 | |
| UnitedStates(UnitedStates::GovernmentBond), | : 使用するカレンダー | |
| faceAmount, | : 額面 | |
| Date(15,August,2013), | : 償還日 | |
| Following, | : 償還日が休日であった場合の取り扱い | |
| Real(116.92), | : 償還価格 | |
| Date(15,August,2003) | : 債券の発行日 |
これらの部品(コンストラクターへの引数)で、2点だけ注意点を。
- 償還価格として 実数値 116.92 が渡されています。通常、ゼロクーポン債は額面の100%で償還されるので、このようにオーバーパーで償還される例はあまり見かけません。その結果、最初の方で示した出力画面で、このゼロクーポン債の価格が 100.92 とオーバーパーになっていました。テストコードなので、気にしないでおきましょう。
- カレンダーとして 米国の政府債用のカレンダーが指定されています。米国では、金融商品によって、取引可能な営業日が若干異なっています。従って、カレンダーの指定は、単に国名として United States を指定するだけではなく、サブカテゴリ―として商品を指定する必要があります。
債券オブジェクトが出来れば、それに価格エンジンを設定します(388行目)。
(2) 固定金利債
次に固定金利債を生成しています。固定金利債は、固定金利のクーポンキャッシュフローを持ちます。従って、このオブジェクトを作るには、クーポン支払日の情報から作る必要があります。
― 391~394行目で Schedule オブジェクトを生成しています。この部品は、クーポン支払日の配列を、指定された取引慣行に従って、自動的に生成するオブジェクトです。Schedule クラスは、前の MulticurveBootstrapping プロジェクトにおいて、VanillaSwap オブジェクトの部品としても使われていました。詳しい説明は Appendix-1 を参照して下さい。
― 396~403行目で、Instrument の派生クラスである FixedRateBond のオブジェクトを生成しています。コードにある通り、コンストラクターに、必要な部品を渡して具体的なオブジェクトが生成されます。コンストラクターが起動されると、具体的なクーポンキャッシュフローが生成されて、内部の変数に保存されます。FixedRateBond クラスと、そのコンストラクターの役割、さらにそこで使われている重要な部品については、Appendix―2 を参照して下さい。 また1本のキャッシュフローをオブジェクトモデル化したCouponクラスについては Appendix-3 を参照して下さい
― 405行目債券オブジェクトが出来れば、それに価格エンジンを設定します
(3) 変動利付債
最後に、変動利付債のオブジェクト(Instrumentの派生クラスである FloatingRateBond クラスのオブジェクト)を生成します。まず、その主要部品を2種類、事前に作成します。すなわち
― 変動金利インデックス(411~412行目) : ここではUSDLiborオブジェクト
― Scheduleオブジェクト(414~417行目)
これらの部品を使って、FloatingRateBond オブジェクトを組み立てます。419 行目にあるこのオブジェクトのコンストラクターを抜き出し、どのような引数(部品)を使って組み立てているか見てみます。
| FloatingRateBond floatingRateBond ( | ||
| settlementDays, | : 取引日から決済日までの期間 | |
| faceAmount, | : 額面 | |
| floatingBondSchedule, | : クーポンの支払日の配列 | |
| libor3m, | : 変動金利インデックス | |
| Actual360(), | : 日数計算方法 | |
| ModifiedFollowing, | : クーポン日が休日の場合の取扱い | |
| Natural (2), | : 金利決定期間(2営業日前) | |
| std::vector<Real>(1, 1.0), | : ギアリング(リバースFloater) | |
| std::vector<Rate>(1, 0.001), | : 変動金利スプレッド | |
| std::vector<Rate>(), | : 金利キャップ | |
| std::vector<Rate>(), | : 金利フロアー | |
| true, | : 金利後決め=True | |
| Real(100.0), | : 償還価格 | |
| Date(21, October, 2005) | : 発行日 | |
| ); |
― この中で、最も重要な部品は、変動金利インデックスで、411 行目で生成された USDLibor インデックスが使われています。USDLibor インデックスを含めた Index クラス全般については、Appendixー4を参照して下さい。
― 引数の中に、日本ではあまり馴染みの無い情報が含まれています。簡単に解説すると
- ギアリング:リバース変動利付債は、下記式でクーポンレートが決められますが、その式の中のギアリングが該当します
\[固定金利 ~- ~ 変動金利~~×~~ギアリング \] リバース変動金利債では、上式から分かる通り変動金利が上昇すると、逆にクーポンレートは下がり、下落するとクーポンが上昇するような変動利付債です。なのでリバースです。 - キャップとフロアー : 変動金利の上限と下限を決めます。
- 金利後決め(in arears) : 変動金利は、通常クーポン期間のスタート日の2営業前に決めます。それを、クーポン期間のエンド日(クーポン支払日)の2営業日前に決める条件です。Coupon in arearsと呼ばれていますが、この条件の変動金利クーポンは、コンベクシティ調整の為に、オプションモデルが必要になります。
上記のように、変動利付債では、クーポンにオプションが付いているケースがあります。その場合、クーポン自体をオブション商品とみなし、クーポンごとに価格計算をする機能が用意されています。その機能は、FloatingRateCouponPricer クラスにカプセル化されています。その具体的な派生クラスで、Coupon に内包しているデリバティブズの価格計算アルゴリズムを定義します。(この機能は、クーポンに付されているオプション等の条件が、それぞれ独立の場合にのみ有効です。)このプログラム例では、
- 443行目で、BlackIborCouponPricerオブジェクトを生成し、
- 447~456行目で、そのCouponPricerにVolatilityデータを与え
- 457行目で、FloatingRateBondのキャッシュフローオブジェクトに、そのPricerをセットしています。
FloatingRateCouponPricer の詳細についても、Appendix―5を参照して下さい。
最後に440行目で、FloatingRateBondにPricingEngineを設定しています。
1.2.4.4.5 価格の計算と画面出力 (470~544行目)
最後に、3種類の債券の価格や経過利息などを計算し出力しています。価格計算は、これまでのプロジェクトの例と同じく、Instrument(と、その派生クラス)に備わっている NPV()メソッドを呼び出すだけです。具体的には、490~492行目で、3種類の債券オブジェクトの NPV()を呼び出しています。
| 490 | << std::setw(widths[1]) << zeroCouponBond.NPV() |
| 491 | << std::setw(widths[2]) << fixedRateBond.NPV() |
| 492 | << std::setw(widths[3]) << floatingRateBond.NPV() |
計算結果は、前ページの最初の方で示した画面出力の通りです。
このプロジェクトでは、NPV()メソッド以外に、債券オブジェクトが備えている以下のようなメソッドを使い、その計算結果を出力しています。
| cleanPrice() | : 経過利息を含まない債券価格 |
| dirtyPrice() | : 経過利息を含んだ債券価格 |
| accruedAmount() | : 経過利息額 |
| previousCouponRate() | : 前回クーポンレート |
| nextCouponRate() | : 次回クーポンレート |
| yield() | : 複利利回り |
コードの解析は以上の通りですが、このBondsプロジェクトでも、
- 金融商品(3種類の Instrument オブジェクト)と価格エンジン(1個の PricingEngine)を、部品から作り上げ、
- PricingEngine を Instrumentに設定し
- Instrument に備わっている NPV()メソッドやその他のメソッドを呼びだし価格計算を行っています。
部品の中で、最も重要なのがイールドカーブ(TermStructureクラスのオブジェクト)ですが、ここでも、コードの半分以上がその組み立てに使われています。
金融商品は、種類によって使われる部品が様々ですが、どういった部品が必要になるかは、QuantLibのReference Manualから、各Instrumentクラス(から派生した具体的な商品のクラス)のコンストラクターの引数を見て確認します。複雑な部品では、部品自体をより小さな部品から作り上げる必要があり、その場合は部品のコンストラクターで、さらにどのような部品が必要か確認します。
このプロジェクト例で使われたいくつかの重要な部品については以下のAppendixで解説します。
1.2.4.4.6 Appendix
Appendix-1 Schedule クラス
金融商品(Instrumentオブジェクト)は、キャッシュフローの集合と看做す事が出来ます。債券やスワップのように、キャッシュフローが決まった間隔(3か月、6か月、あるいは1年)で多数発生する場合、キャッシュフロー発生日を特定するクラスが用意されています。それが Scheduleクラスになります。キャッシュフロー発生日の決め方は、商品によって、取引慣行で決まっていたり、あるいはスワップのように、取引ごとに個別の契約で決めたりします。いずれも一定のルールに従ってスケジュールを特定するので、そのルールを取り込み、具体的なスケジュールを生成するのが Scheduleクラスです
Schedule のコンストラクターにどのような引数(部品)を渡して、具体的な Scheduleオブジェクトが作られるか、見てみます。Bondsプロジェクトの391行目にある Schedule のコンストラクターを抜き出しました。
| Schedule fixedBondSchedule ( | |
| Date(15, May, 2007), | : 発行日 |
| Date(15,May,2017), | : 償還日 |
| Period(Semiannual), | : クーポン支払い回数/年 |
| UnitedStates(UnitedStates::GovernmentBond), | : カレンダー (米国:政府債営業日) |
| Unadjusted, | : 休日の場合の調整(クーポン日) |
| Unadjusted, | :休日の場合の調整(償還日) |
| DateGeneration::Backward, | :クーポンスケジュールの生成方法 |
| false | :クーポン日が月末の場合の調整 |
| ); |
クーポン日のスケジュールの決め方は、主に、発行日を基準に決める方法と、償還日を基準に決める方法があります。年2回払いであれば、
発行日を基準に、発行日から6か月後、1年後、1年6か月後・・・
償還日を基準に、償還日から6か月前、1年前、1年6か月前・・・
と応当日を決めていきます。上記のコンストラクターでは DateGeneration::Backwardと指定し、後者の基準で具体的なスケジュールが決められています。
また、上記の方法でスケジュールを生成する際、応当日が休日であった場合に支払日をどう調整するかも、取引慣行で決まっています。上記では、クーポン日、償還日についてそれぞれ Unadjusted と設定されています。これは、6か月分のクーポン額を計算するにあたって、クーポン日が休日で実際の支払日が翌営業日になったとしても、その期間のクーポン額は調整しない事を意味します。休日の特定は、引数で渡されたカレンダーに従います。
さらに、債券の期間(年数)に端数がある場合、上記の方法でクーポン日を決めると、最後(あるいは最初)のクーポン期間がちょうど6か月にならない場合があります。その場合、その期間を通常の期間より長めにとるのか、短めにとるのか選択する必要があります。その設定は、コンストラクターに、その情報(最後のクーポン日あるいは最初のクーポン日)を指定する必要があります。上記のコンストラクターでは、その情報はみられませんが、その場合はデフォールトで決まった方法が使われます。
このように、QuantLib を使いこなすには、Instrument や PricingEngine が、どのような部品で作られているか、Reference Manual でコンストラクターの引数を確認する必要があります。さらに、大きな部品であれば、部品自体のコンストラクターの引数を確認して、それがどのような部品の部品で作られるか確認する必要があります。さらに、この Schedule クラスの例で示した通り、部品を特定するには、取引慣行や個別の契約内容を確認する必要があります。すなわち、かなり詳細な実務知識が必要になります。ただ、それを知ってさえいれば、あとは QunatLib ライブラリーの中から必要な部品を選べばいいだけです。QuantLib は欧米や日本といった主要な金融市場で取引されている金融商品の大半の取引慣行をオブジェクトモデル化し、クラスライブラリーとして提供しています。それらをライブラリーの中から探すだけで、わざわざ自分でコードを開発する必要はありません。
Appendix-2 FixedRateBond クラス
QuantLib において、Instrument クラスのオブジェクトが果たす主な役割は、金融商品のキャッシュフローの情報を保持する事です。Instrument の派生クラスである FixedRateBond クラスの役割もそれがメインになります。このクラスは、引数としてキャッシュフローを生成する為に必要な情報(部品)を受け取ります。上記で説明した、Schedule オブジェクトもその一つで、その受け取った情報(部品)を使って、コンストラクターが具体的なキャッシュフローを組み立てます。
実は、FixedRateBond クラスは、コード例にあるのと別のコンストラクターも用意されています。そこでは Schedule オブジェクトを別に作成するのではなく、Scheduleオブジェクトの生成に必要な情報をFixedRateBond のコンストラクターに渡して、そのコンストラクターの中で作ってしまうものです。そのコンストラクターのコードを fixedratebond.cpp ファイルから抜粋したものを下記します。引数の中に、先ほど説明した Schedule のコンストラクターで使用したのと同じ情報が含まれているのが分かります。
FixedRateBond::FixedRateBond(Natural settlementDays,
const Calendar& calendar,
Real faceAmount,
const Date& startDate,
const Date& maturityDate,
const Period& tenor,
const std::vector<Rate>& coupons,
const DayCounter& accrualDayCounter,
BusinessDayConvention accrualConvention,
BusinessDayConvention paymentConvention,
Real redemption,
const Date& issueDate,
const Date& stubDate,
DateGeneration::Rule rule,
bool endOfMonth,
const Calendar& paymentCalendar,
const Period& exCouponPeriod,
const Calendar& exCouponCalendar,
const BusinessDayConvention exCouponConvention,
bool exCouponEndOfMonth)
: Bond(settlementDays,
paymentCalendar==Calendar() ? calendar : paymentCalendar,
issueDate),
frequency_(tenor.frequency()), dayCounter_(accrualDayCounter) {
maturityDate_ = maturityDate;
Date firstDate, nextToLastDate;
switch (rule) {
case DateGeneration::Backward:
firstDate = Date();
nextToLastDate = stubDate;
break;
// other cases 省略
default:
QL_FAIL("unknown DateGeneration::Rule (" << Integer(rule) << ")");
}
Schedule schedule(startDate, maturityDate_, tenor,
calendar, accrualConvention, accrualConvention,
rule, endOfMonth,
firstDate, nextToLastDate);
cashflows_ = FixedRateLeg(schedule)
.withNotionals(faceAmount)
.withCouponRates(coupons, accrualDayCounter)
.withPaymentCalendar(calendar_)
.withPaymentAdjustment(paymentConvention)
.withExCouponPeriod(exCouponPeriod,
exCouponCalendar,
exCouponConvention,
exCouponEndOfMonth);
// other construction of member variables 省略
}
さて、せっかくコンストラクターの中身を示したので、そこで行われている Schedule の作成以外に、もうひとつ重要な部分を説明したいと思います。それは、その金融商品の具体的なキャッシュフローを生成する部分です(上記コードの最後にある cashflows_=FixedRateLeg(…) の部分です。)
ここでは、キャッシュフローの配列である Leg クラスのオブジェクト(変数名cashflows_)を生成しています。デザインパターンに馴染みのある方は、Factory Method パターンが使われてるのが分かると思います。すなわち、FixedRateBond クラスは、具体的なキャッシュフローを組み立てる工程を、FixedRateLeg クラスという組み立て工場(Factory)に下請けに出しています。FixedRateLeg オブジェクトは、ここでは見えませんが、背後で Coupon オブジェクトの配列(すなわちキャッシュフロー)を生成しています。Coupon オブジェクトは、1本のキャッシュフローを具体化したオブジェクトですが、これについては、次の Appendix-3 で説明します。
Appendix-3 Couponオブジェクトについて
ここでは、債券のキャッシュフローの基本単位である、Couponクラスについて、少し説明したいと思います。
Couponクラスの派生元、派生先は、下記のチャートのようになっています。(QuantLib の Reference Manualから抜粋)
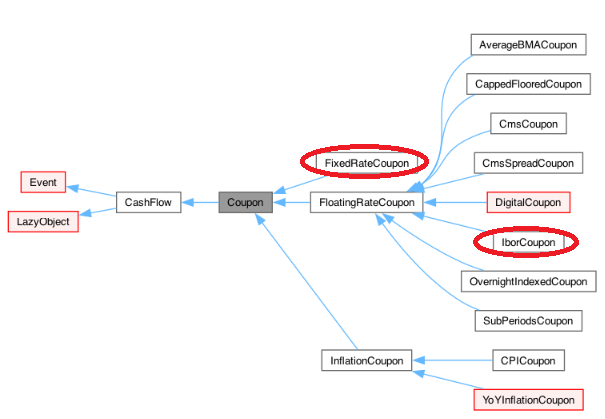
ベースクラスとなっているEventクラスですが、特定の日付に発生する経済事象を抽象化したクラスです。経済事象とは、Cash Flowの発生や、オプション期日の到来、オプションの行使、などが想定されます。従って、このクラスのメインのインターフェースは、そういった事象が発生したか否かを返すhasOccured( )と、その発生日付を示すdate( )になります。
そして、そこから派生する CashFlow クラスは、読んで字のごとく、Cash Flow の発生事象を抽象化したクラスです。Cash Flow の構成要素は、“日付”と“金額”になりますが、この階層では、いずれの情報もメンバー変数として持っていません。しかし、純粋仮想関数としてamount( )メソッドが宣言されており、その内容を派生クラスで実装する必要があります。このメソッドの機能は、名前から明白で、Cash Flow の金額を返します。
そして“Coupon”クラスがそこから派生しています。実は、この階層でもまだ抽象クラスで、このクラスのオブジェクトを作る事はできません。このクラスは、債券のクーポン属性をオブジェクトモデル化したクラスです。債券のクーポンに共通する属性として思い浮かぶものを挙げてみると、“クーポンレート”、“クーポン計算期間”、“クーポン支払日”、“クーポン日が休日の取扱い”、“クーポン金額”、“経過利息の計算”、などがあります。従って、このクラスは、こういった属性の情報にアクセスできるインターフェースと、メンバー変数を持ちます。ところが、肝心の“クーポンレート”を保持するメンバー変数がありません。上記のチャート図にある通り、このクラスから、さらにクーポンのタイプを細かく類型化し、具体的な派生クラスを作り、そこで保持するようになっています。
Coupon の派生クラスのひとつが“FixedRateCoupon”クラスです。ここで初めて具体的なオブジェクトを生成する事が出来ます。固定金利クーポンの属性や計算機能をカプセル化したクラスです。メンバー変数として、InterestRate クラスの変数 rate_ を持ちます。この変数の意味は名前から明白です。この値を使って、Coupon クラスで宣言された様々なインターフェースの実装が行えます。InterestRate クラスは、金利に関する meta-data を保持するクラスです。金利は、例えば年率2.5%と表示されていても、複利の回数や、日数計算方法の違いによって、実際に支払われる金額が異なってきます。そういった情報も含めて、金利の情報をカプセル化したクラスが InterestRate クラスになります。
Appendix-4 Indexクラス
コード例に使われている USDLibior インデックスは、Libor クラスの派生クラスで Libor クラスは、IborIndex → InterestRateIndex → Indexクラスの派生クラスですす。ベースクラスとなる Indexクラスから、様々な派生クラスが派生する様子を、Reference Manual から抜き出しました。
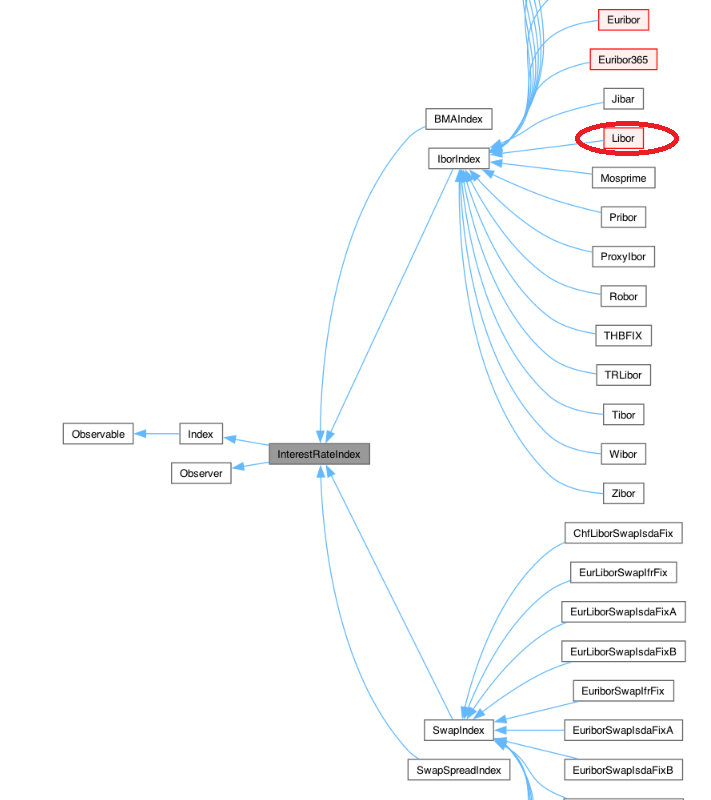
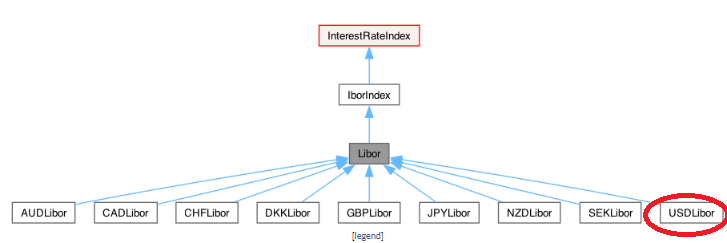
Index クラスは、金融指標(金利、株式、為替、債券などの指標)の属性をカプセル化したクラスです。このベースクラスは、抽象クラスで、ここで宣言されているメソッドはほとんど、純粋仮想関数です。それらのメソッドは、すべての Index に共通する、インデックスの値の設定と、設定された値へアクセスする関数になります。
このベースクラスから、‘金利’に関するインデックスを取り扱うクラスとして、InterestRateIndexクラスが派生しています。金利に関するインデックスは、LIBORのようなロンドン市場におけるインターバンク金利以外にも、コール金利、Federal Fund 金利、Swap 金利、など様々な金利関連商品のインデックスがありますが、InterestRateIndex は、それらすべてをカバーするベースクラスになります。このクラスが提供しているインターフェースや、格納しているメンバー変数は、これらの金利インデックスすべてに共通するものです。
さらに、このクラスから IborIndex クラスが派生しています。Ibor は、Inter-Bank Offer Rate の略で、銀行間の資金市場(Inter-Bank Money Markets)における、資金の出し手が呈示する金利(Offer Rate、すなわち貸出金利)のことです。
LIBOR クラスは、IborIndex からさらに派生したクラスです。ロンドンのインターバンク資金市場における取引慣行などをカプセル化したクラスになります。そこから、通貨ごとのクラスが派生し、それが最終的に具体的なクラスになります。このテストプログラムでも、最終的に USDLibor クラスのオブジェクトを生成しています。
Index クラスは、あくまでインデックスの‘Fixing に必要な情報’や、‘Fixingの方法’をカプセル化したクラスで、Fixing 後のデータを保持するクラスでは無い点に注意して下さい。このクラスのクラス階層の、どの段階にもFixingされた指標の値を保持するメンバー変数はありません。実は、Fixing後のデータは、IndexManagerと呼ばれるクラスのインスタンスに、すべてまとめて保管されています。この Example のコードには出てこないので、その説明は省略します。
Index クラス全体の説明は、Luigi Ballabio氏の“Implementing QuantLib”の中の”Odds and Ends“の中で、解説している部分があるので、そちらを参考にして下さい。IndexManagerについても、説明があります。 また、その日本語訳はこちら。
ちなみに、かつて変動金利インデックスの主流であったLIBORは、もはや使われなくなったのはご存知だと思います。
Appendix-5 FloatingRateCouponPricerの生成
FloatingRateCouponPricer について、少し説明したいと思います。変動利付債のクーポンに Cap や Floor が付いている場合、クーポン自体が一種の金利オプションであり、その価格計算には、何等かのオプション価格計算のエンジンが必要になります。それが、この FloatingRateCouponPricer になります。従って、これは一種の簡易版価格エンジンで、それが個別の FloatingRateCoupon オブジェクト毎に設定されます。
下記に、FloatingRateCouponPricer の派生クラスのダイアグラムを載せますが、それを見てみると、通常の Cap/Floor 付きクーポンで使われる BlackIborCouponPricer や、CMS リンクのクーポンで使われる CmsCouponPricer などが見当たります。
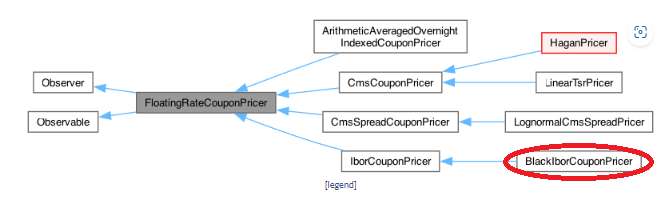
このプロジェクトでは、443行目で、BlackIborCouponPricer クラスのインスタンスを生成しています。オプションの価格を計算するには、パラメータとして Volatility の情報が不可欠であり、446 から 454行目で、その Volatility の Term Structure オブジェクトを生成しています。しかし、ここでは、Volatility の値が 0 に設定されており、オプションの価格計算上、意味の無い値になっています。テスト用なので適当な数字にしたのでしょう。
<ライセンス表示>
QuantLibのソースコードを使う場合は、ライセンス表示とDisclaimerの表示が義務付けられているので、添付します。 ライセンス