1. QuantLibを使ってみる
1.2 Example を試す
1.2.6 : BermudanSwaption : 3種類のShort Rate Modelを使ったバーミューダン・スワップションの価格評価
1.2.6.1 はじめに
ここでは、QuantLib のテスト用プロジェクト、BermudanSwaption について解説します。このプロジェクトの解説は、既に2021年に Web に上げていましたが、その後、C++11 への移行に伴いソースコードが若干書き換えられたので、解説もアップデートしました。
このプロジェクトは、3種類の Short Rate Model (G2++、Hull-White、Black-Karasinski)を使って、バーミューダン・スワップションの価格評価を行っています。前のプロジェクト CallableBonds でも、バーミューダンタイプの Call Option付き債券の価格を、Hull-White モデルを使った価格エンジンで導出しました。しかしそこでは、モデルのパラメータを Calibration で求めるのではなく、適当な値を外生的に与えていました。
ここでは、3種類の Short Rate Model それぞれについて、モデルパラメータを、ベンチマークとなる Swaption 価格に Calibration してから、価格評価を行っています。実務でパラメトリックなモデルを使う場合、パラメータの Calibration は必須です。ここでテストされる3種類の Short Rate Model は、すべて CalibratedModel から派生しており、このベースクラスで、Calibration のアルゴリズムが用意されています。このプロジェクト例で、それが具体的にどのように使われているか、学べると思います。
ちなみに、Short Rate ModelのパラメータCalibrationは、2つの別々のアルゴリズムが必要です。すなわち
- イールドカーブに、中心回帰レベルをフィットさせるアルゴリズム
- ベンチマーク商品の価格(あるいはVolatility) に、中心回帰強度と Volatility パラメータをフィットさせるアルゴリズム
このプロジェクトで例示されているのは、2.の方のアルゴリズムです。1.のイールドカーブへのフィットは、価格エンジンの中に組み込まれており、価格エンジンを起動するたびに、自動的に行われます。なので、ユーザーは、そちらの方は気にしなくていいでしょう。
ここで使われている、3種類のShort Rate Modelについて、簡単に解説しておきます。Short Rate Modelのファミリーは、瞬間短期金利の確率過程を記述するもので、一般的に下記のような確率微分方程式で記述されます。
\[ dr(t)=k(t)(θ(t)-r(t))dt+σ(r,t)dW(t) \]但し
\(r(t)\) : 瞬間短期金利
\(k(t)\) : 中心回帰強度
\(θ(t)\) : 中心回帰レベル
\(σ(r,t)\) : 拡散係数(Volatility)
\(dW(t)\) : ウィーナー過程
上の式は、Short Rate Model を一般化した表記方法で、各パラメータ係数の違いが、個別の Short Rate Model を特徴付けます。
(a) Hull-Whiteモデルについては、前のプロジェクトで既に解説済なので飛ばします。
(b) Black-Karasinskiモデルは、瞬間短期金利が、中心回帰する幾何ブラウン運動すると仮定したモデルです。但し、ここでは中心回帰強度 \(k(t)\) と、拡散項係数 \(σ(r,t)\) は、それぞれ定数と仮定したモデルを使っています。このモデルは、短期金利 \(r(t)\) がマイナスになる事が無いので、当初はそれが Hull-White モデル対する優位点とされていました。一方で、このモデルからは、ゼロクーポン債価格や、オプション価格が解析的に求まらず、価格計算には有限差分法や、3項Tree などを使って、数値的に(近似値を)求める必要があります。このモデルや、これに類似する Short Rate Model のグループは、90年代に、実務でも使われていたようですが、主要国で超低金利、あるいはマイナス金利が状態化した今、このモデルをそのままの形で使っている所は無いと思います。
(c) G2++モデルは、確率変数が 2ファクターの Short Rate Model で、瞬間短期金利 \(r(t)\) が、ガウス分布する2つの確率変数\(~x(t),~y(t)~\)とイールドカーブへのフィッティングパラメータ \(φ(t)\) の和として、下記のような確率微分方程式で表現されるモデルです。
\[ \begin{align} & r(t)=x(t)+y(t)+φ(t), \\ & dx(t)=-a x(t)dt+σ dW_1 (t),~~~~~~ x(0)=0 \\ & dy(t)=-b y(t)dt+η dW_1 (t),~~~~~~ y(0)=0 \\ & Corelation(dW_1 (t),~dW_2 (t))=ρ dt \end{align} \]\(dx~と~dy~\)はいずれも 0 に中心回帰するドリフト項と、それぞれ\(σ,~η\) の Volatility 係数を持つ拡散項で記述されています。このモデルのパラメータは、\(φ(t),~a,~b,~σ,~η,~ρ\) で、\(φ(t)\) はイールドカーブにフィットするように Calibration され、\(a,~b,~σ,~η,~ρ~\) は、市場の Volatility データに Calibration されます。このプロジェクト例では、後者の Calibration を行っています。
Short Rate Model については、すでにある程度理解されているという前提で話を進めるので、ここでは、これ以上詳しく解説しません。より詳しい説明は上級編 “Short Rate Model”を参考にして下さい。た G2++ については、Brigo-Mercurio “Interest Rate Models”(2006, Springer)に詳しく解説されています。
この プロジェクト例では、いずれのモデルのパラメータも、時間に依存せず、定数と仮定されています。パラメータを時間の関数(通常は、Piecewise Constant な関数と仮定される)とすれば、市場データへのフィットは良くなりますが、デメリットも多くあります。実務では、定数と仮定して使う事の方が多いように思います。時間に依存する関数と仮定して Calibration する方法は、Gaussian1DModel で解説する予定です。
イントロダクションの最後に一点述べておきます。このプロジェクトでは、変動金利インデックスとして 6か月EURIBOR が使われています。ご承知の通り、LIBOR や EURIBOR などの金利指標はもはや使われなくなっています。実際に QuantLib を使う際は、これらはすべて最新のOISインデックスに入れ替えて使う必要があります。
1.2.6.2 ソースコードのコンパイルと実行
これまでと同様、まずBermudanSwaptionプロジェクトのソースコードをビルドし、実行可能なバイナリーファイルを生成します。その手順は以下の通りです。
- まず QuantLib ディレクトリ下にある“QuantLib.sln”ファイルを開けます。すると Visual Studio が起動され、このソリューションファイルが開かれます。ソリューションエクスプローラーにある 21個のプロジェクトのリストから、BermudanSwaption プロジェクトを選択します。
- メニューバーから、“プロジェクト(P)” → “スタートアッププロジェクトに設定(A)” を選択します。これにより BermudanSwaption プロジェクトが、21個のプロジェクトの中で、最初に実行されるプロジェクトになります。
ここからのビルド方法は、QuantLib.sln ファイルのビルド、EquityOption プロジェクトのビルド、の所で何度か解説しているので、そちらを参考にして下さい。そこで解説した通り、Boost ライブラリーへのパスの設定を忘れずに行って下さい。
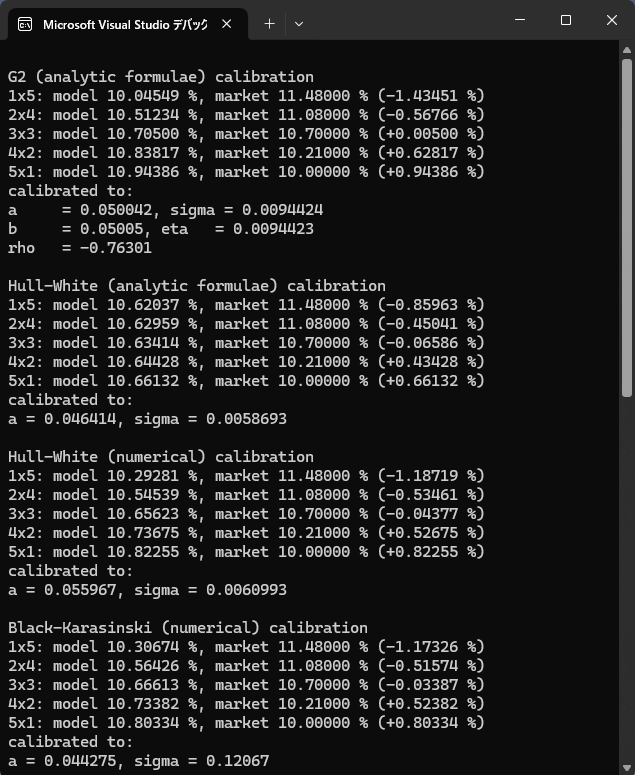
ビルドが成功すれば、試しにプログラムを走らせてみます。メニューバーから“デバック(D)” → “デバックの開始(S)”を選択します。下記の コンソール画面が出力されれば成功で
(但し、プログラムが終了すると同時にConsole画面も消えてしまうようであれば、メニューバーから、ツール→オプション→デバック→全般を選択し、「デバックの停止時に自動的にコンソールを閉じる」のチェックボックスをはずします。)
計算時間は、数分かかります。計算時間の多くは、G2++モデルの価格エンジンのアルゴリズムによるものと推察されます。G2++モデルは、2ファクターモデルになるので、有限差分法や3項Treeのアルゴリズムでは、1ファクターモデルと比べて、N を時間軸のステップ数とすると、\(O(N^2)\)のオーダーで計算時間がかかります。
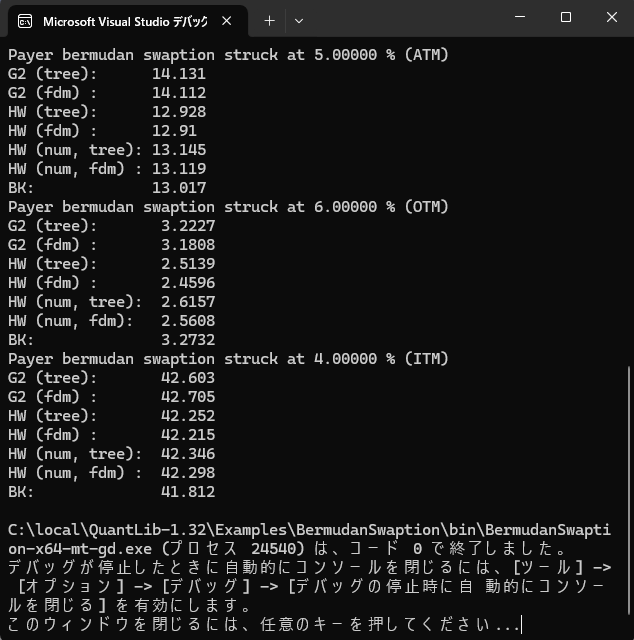
コンソール画面出力
1.2.6.3 ソースコードの全体像
ソリューションエクスプローラーにある BermudanSwaption プロジェクトを展開すると BermudanSwaption.cpp というファイル名のソースコードファイルが現れます。それを、ブラウザーでも見られるように、htmlファイルに変換したソースコードを載せますので、それを見ながら読み進めて下さい。
ソースコードは約300行あります。その構成は、下記のようになっています。
| ― プリプロセッサ- | (22~45行目) |
| ― Calibration用のデータと関数の定義 | (49~89行目) |
| ― メイン関数 | (91~363行目) |
| ・本体 | (93~356行目 try{}で囲まれた部分) |
| ・例外処理/td> | (357~363行目 catch{}部分) |
メイン関数の本体部分は、これまでのプロジェクト例と同様、下記のような作業を行っています。
- 商品オブジェクトと価格エンジンの部品をそれぞれ作成し、
- 部品を組み立てて商品オブジェクトと価格エンジンを作成
- 価格エンジンを商品オブジェクトにセットして価格計算を実行
- 計算結果を画面出力
但し、特にこのプロジェクトでは、それらに加えて、2.と3.のステップの間に価格エンジンで使われるモデル(Short Rate Model)の、パラメータの Calibration を行っています。
Calibration のアルゴリズムは、ベンチマーク商品(ここではヨーロピアン・スワップション)の価格を、ベンチマークモデル(ここでは Shifted Lognormal モデル)と、Calibration 対象となるモデル(ここでは3種類のShort Rate Model)で計算し、その差が最小となるようなパラメータを求めるものです。言い換えると目的関数の最小値問題を解いてパラメータを求めるものです。このアルゴリズムを実装しているCalibratedModelクラスの calibrate()メソッド、及びそこで使われている CalibrationHelper クラスについては、別途 Appendix でより詳しく説明します。
バーミューダン・スワップションの価格計算は、解析解では求まらず、有限差分法や3項Tree といった数値解を求めるアルゴリズムが必要になります。このプロジェクト例では、G2++ と Hull-White モデル(解析解モデルと数値解モデルの2種類)については、有限差分法を使ったアルゴリズムと3項Tree を使ったアルゴリズムの2種類の価格エンジンをテストしています。Black-Karasinski モデルについては、3項Tree を使った価格エンジンのみをテストしています。
<ライセンス表示>
QuantLibのソースコードを使う場合は、ライセンス表示とDisclaimerの表示が義務付けられているので、添付します。 ライセンス