実務で使える金融工学　実践編

１.  QuantLibを使ってみる

1.2   Example を試す

1.2.5   CallableBonds :　Call Option付き債券の価格評価 (続き)

1.2.5.4   ソースコードの解析

ではソースコードの中身を詳細に見ていきます。 

1.2.5.4.1   ローカル関数の定義（43～68行目）

このプロジェクトでは、main()関数の前に、ローカル関数 flatRate()を2種類（オーバーロードさせて）定義しています。この関数は、イールドカーブ構築に必要なデータを引数として与えてやると、全期間同一レートとなるフラットなイールドカーブを返します。債券の利回りは、通常、フラットなイールドカーブを前提としたＩＲＲ(Internal Rate of Return:内部収益率)の概念を使って表現されるので、期間構造を勘案したイールドカーブは使いません。 

Main()関数本体の中で、この関数にデータを与え、フラットなイールドカーブを構築しています。 

1.2.5.4.2　  時価評価基準日の設定

76，77 行目で、本日の日付と時価評価基準日（evaluationDate）を設定しています。これまでのプロジェクト例で解説した通り、時価評価基準日は、グローバル変数として、Settingクラスのオブジェクトに情報が保持されます。 

ここでは、時価評価基準日として「本日」が設定されています。ところが、債券の時価評価基準日は、通常、債券の決済日が使われます。（前のbondsプロジェクト例では、そうなっていました）　QuantLibでは、時価評価基準日は、Singletonパターンを使ったSettingオブジェクト内で１つしか設定できないので、デリバティブズと債券の価格計算を同時に行う場合は注意が必要です。 
　（注： Singleton パターン（デザインパターンのテクニックの一つ）をつかった Settings クラスについては、Luigi Ballabio氏の Implementing QuantLib の Odds Ends の中で詳しく解説されています。 その日本語訳は こちら。 ）

79～85行目で、コンソール画面への出力が記述されています。その内容は、このテストプログラムは、BAC4.65 09/15/12 ISIN: US06060WBJ36　という実際に存在する債券の価格評価を行い、それを、Bloombergの計算結果と比較する、というものです。

（注：実在する債券は、BAC（Bank of America Corp. の略称）発行の、クーポンが4.65％、満期が2012年9月15日のコールオプション付き固定債です。ISINは、International Securities Identification Numberの略で、国際的に統一された証券特定番号です。このプロジェクト例が作成されたのが20年近く前なので、この証券はすでに償還されています。） 

1.2.5.4.3　商品オブジェクトと価格エンジンの生成

　98～172行目までは、以下の作業を行っています。 

• 商品オブジェクトの部品と価格エンジンの部品の生成
• 価格エンジンの構築
• 商品オブジェクトの構築

ここで生成される商品オブジェクトは CallableFixedRateBond クラスのオブジェクトです。このクラスの階層構造は以下のようになっています。 

Instrument ← Bond ← CallableBond ← CallableFixedRateBond 

このクラスは、クラス名から判る通り、コールオプション付き固定金利債をオブジェクトモデル化したものです。このオブジェクトの生成も、これまでのプロジェクトと同様に、オブジェクトに必要な部品からまず作成します。そうやって揃えた部品を CallableFixedRateBond のコンストラクターに渡してオブジェクトが完成します。ここでは部品の生成の解説は飛ばし、一気に商品オブジェクトの生成の所に行きます。 

168行目にある、この商品のコンストラクターを下記します。各引数が部品になりますが、コードを見れば分かる通り、それぞれ事前に作成されています。 

CallableFixedRateBond   callableBond (
	settlementDays,		：決済日までの営業日日数
	faceAmount, 		：額面
	sch,				：クーポンスケジュール
	vector(1, coupon),		：クーポンレート
	bondDayCounter,		：日数計算方法
	paymentConvention,	：クーポン日が休日の場合の取り扱い
	redemption, 		：償還価格
	issue,				：発行日
	callSchedule			：コールオプションの行使日のスケジュール
	);	

各引数（オブジェクトを組み立てる為の部品）を、どこでどのように作成しているかは、コードで確認して下さい。特に、債券の情報として重要な、満期日とか、休日の取り扱いとか、カレンダーなどは、sch（Scheduleオブジェクト）の中に情報として取り込まれているのを確認して下さい。 

さて、コンストラクターに渡された最後の引数である callSchedule は、コールオプションの行使日のスケジュールを具体化したオブジェクトです。110 から 125行目で、その情報を持つ CallabilitySchedule オブジェクトを生成しています。このクラスは、Callability クラスの配列です。配列の要素である Callability オブジェクトは、それぞれ一個のオプションの情報をカプセル化しています。具体的には、Put/Call のタイプ、償還価格、および行使日の情報です。この例では、各クーポン日にオプション行使が可能となっているので、合計で 24回のコール日付が設定されています。従って、それぞれに対応する 24個の Callability オブジェクトが生成され、それが CallabilitySchedule 配列に格納されています。 

さて価格エンジンですが、オプションの価値を計算する必要があるので、金利の確率過程を記述するモデルが必要になります。この例では、Hull-White モデルを使って、3項Tree のアルゴリズムをカプセル化したエンジンを使っています。 

164行目の Hull-White モデルオブジェクトのコンストラクターと、166行目の、それを使った 3項Tree の価格エンジンのコンストラクターを下記します。 

164  	auto hw0 = ext::make_shared<HullWhite>(
		termStructure,		：イールドカーブ
		reversionParameter,	：中心回帰パラメータ
		sigma				：金利のVolatility（ガウス分布）
		);				

166  	auto engine0 = ext::make_shared< TreeCallableFixedRateBondEngine> (
		hw0,				：モデル
		gridIntervals			：3項Treeにおける時間軸のステップ数
		);				

（注：型宣言で使われている auto は、C++11で導入されたもので、変数への代入演算子=の右辺から、変数の型が特定できる場合、自動的にその型の変数にするものです。）

Hull-White モデルのコンストラクターには、モデルのパラメータが渡されています。　また、このモデルを使った 3項Tree のアルゴリズムによる価格エンジンには、3項Tree における時間軸方法のステップ数が引数として渡されています。Hull-White モデル、中心回帰強度と、短期金利の Volatility パラメータは、実務では CAP/Floor や Swaption といった商品の価格に Calibration して求めます。しかしここでは、それらが既に Calibration 済みとして、適当な値を外生的に与えています。  

Hull-White　モデルや、３項Treeを使ったアルゴリズムについての詳細な解説は　上級編　Short Rate ModelーHull-White Model を参考にして下さい。ただ、このモデルがQuantLibの中で、どのようなクラスとして設計されているかについては、後述のAppendixを参照して下さい。  

1.2.5.4.4   　価格の計算

以上で、商品オブジェクト（CallableFixedRateBondオブジェクト）と価格エンジンオブジェクト（TreeCallableFixedRateBondEngineオブジェクト）が完成しました。後は、商品に価格エンジンをセットし、計算を実行するだけです。 

このプロジェクトでは、Hull-Whiteモデルで使うVolatilityの水準を５通り（0％, 1%, 3%, 6%, 12%）用意し、それぞれの債券価格と利回りを計算しています。また、その計算結果を、Bloombergの価格計算機能を使った計算結果と比較しています。Bloombergの価格計算機能も、Hull-Whiteモデルを使った3項Treeアルゴリズムなので、計算結果はほぼ同じになりました。（上記の画面出力参照） 

既に述べましたが、Hull-Whiteモデルで使われるVolatilityは、金利の水準自体のVolatilityであって、変化率Volatility（Black Volatility）ではありません。なので、テスト値に使われている６％とか１２％とかの数値は、実際にはあり得ない様な高い水準です。おそらく、テストプログラムを作成した人が、Black Volatilityと混同したのでしょう。でも、なんとか価格は計算できてます。（このテスト値だと、金利がマイナスになる確率がかなり大きくなりますが、その場合でもエラーにならず、許容されているのでしょう。） 

 

<   Hull-Whiteモデル　クラス >

ここで、価格エンジンで使われているHull-Whiteモデルのクラスが、QuantLibの中で、どのように設計されているかについて少し説明します。 

Hull-Whiteモデルは、ご存知の通り、瞬間短期金利の確率過程を、下記の式でモデル化したものです。 

\[ dr(t)=a(θ(t) - r(t))dt+σ~dW(t) \]

この式は、瞬間短期金利 \( r \) が、中心回帰の傾向があるガウス分布する確率過程（Ornstein-Uhlenbeck 過程）を取ると仮定しています。\(θ(t)\) が中心回帰レベル、\(a\) が中心回帰強度になります。 

中心回帰レベル \(θ(t)\) は、市場のイールドカーブから導出される瞬間フォワード金利カーブに Calibration されます。また中心回帰強度 \(a\) と拡散項の係数 \(σ\) は、市場で観測される金利オプションの価格に Calibration されます。従って、このモデルを使って金利オプションの価格計算を行うには、事前に、イールドカーブと、CAP や Swaptionなどの金利オプションの市場データを集めて、そのデータに Calibration しておく必要があります。但し、このプログラム例では、パラメータを既に計算済とみなして外生的に設定しています。 

さて、このHull-White モデルが、QuantLibの中で、どのようにオブジェクトモデル化されているか、見てみます。まず、このプロジェクトで使われているHullWhiteクラスの継承関係は以下のようになっています。 

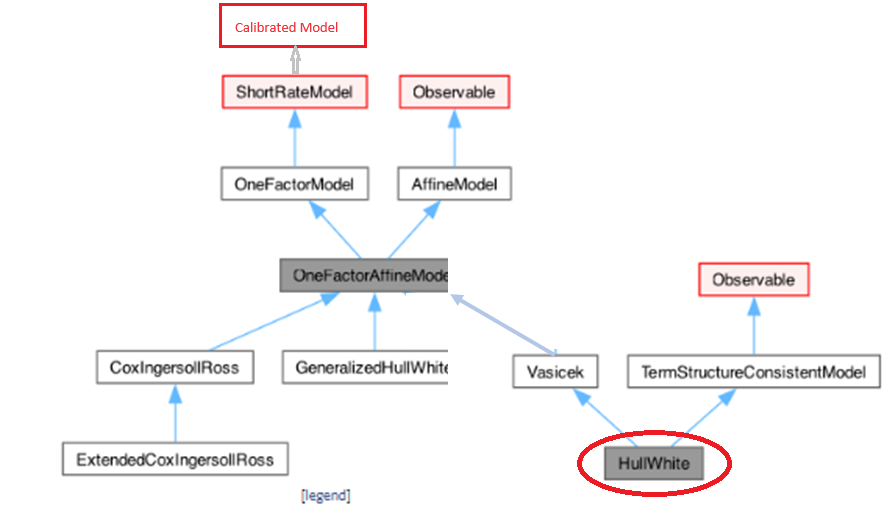
すなわち、このクラスは 3種類のベースクラス、AffineModel、ShortRateModel、および TermStructureConsistentModel から派生しています。ShortRateModel クラスは、さらに CalibratedModel クラスから派生しています。その役割については、BermudanOption のプロジェクトの中で説明する予定で、ここでは飛ばします。 

以下にこの３種類のベースクラスの役割について簡単に解説します 

(a) ShortRateModel　クラス

Short Rate Modelと呼ばれるモデル群は、瞬間短期金利の確率過程をモデル化し、そこから将来のイールドカーブ全体の形状や変動の様子を導出するものです。Vasicekモデルを嚆矢とし、Cox-Ingersol-Rossモデル、Hull-White モデルやBlack-Karasinski、Black-Derman-Toyモデル、などがこのグループに含まれます。

Short Rate Modelは、瞬間短期金利の確率過程を、一般的に次の様な形で表現したものです。 

\[ dr(t)=α(t,r(t))dt+σ(t,r(t))dW(t) \]

ドリフト項の係数 \(α(t,r(t))\) と、拡散項の係数 \(σ(t,r(t))\) の関数形に様々なバリエーションがあり、それがモデルの違いとして現れます。 

従って、Short Rate Model をオブジェクトモデル化するには、まずこの瞬間短期金利の確率過程を共通のベースクラスとするのは自然です。それが、ShortRateModel ベースクラスになります。ここから派生するクラスで、具体的なドリフト項係数や拡散項係数を定義していきます。但し、直下の派生クラスで具体化するのではなく、少しずつ具体化されたクラスを間にはさんで、最終的に具体的モデルが特定されたクラスに行きつきます。その中間にある抽象クラスとして、確率変数をひとつだけ考えるOne Factor Modelのグループと、２つ考えるTwo Factor Modelのグループがあります。Hull-Whiteモデルは、このOneFactorModelからさらに派生しています。 

(b) TermStructureConsistentModel　クラス

Short Rate Modelのドリフト項については、大半のモデルが中心回帰すると仮定されています。その中心回帰レベルは、市場レートから導出される瞬間フォワード金利を基準に決められます。従って、ドリフト項のパラメータを特定するためには、イールドカーブの情報が必要になります。 TermStructureConsistentModel クラスが、その情報を保持し、HullWhiteクラスは、そこからも派生しています。　Hull-Whiteモデルの中心回帰レベルは、θ(t)になりますが、この値を市場のイールドカーブに Calibration して求めます。 

(c)   AffineModel クラス

Hull-White　モデルは、Affine Term-Structure　モデルとも呼ばれており、AffineModel　というベースクラスからも派生しています。Affine Term-Structure Model　とは、ゼロクーポン債利回りが、下記のような形の瞬間短期金利のアフィン関数（一次式）で表現できるモデルの総称です。（注：ここでの　ZeroRate　は連続複利利回りを意味します） 

\[ ZeroRate(t,T)=α(t,T)+β(t,T)r(t) \]

ゼロクーポン債の利回りが求まれば、ゼロクーポン債価格は、下記式で求まります。 

\[ P(t,T)=\exp⁡(-ZeroRate(t,T)*(T-t)) \]

このように、このクラスのモデルでは、ゼロクーポン債価格が、瞬間短期金利から解析的に求まります。 

Hull-White モデルを、実際のオプション価格計算で使うには、まずモデルのパラメータを市場のイールドカーブと、Cap や Swaption の市場価格に Calibration する必要があります。中心回帰パラメータ θ(t) が、イールドカーブに Calibration され、中心回帰の強度パラメータ a と、拡散項の係数 σ が、Cap・Swaption の Implied Volatility に Calibrationされます（但し、先ほど説明した通り、このプロジェクト例では、\(a~ と~σ\) を、外生的に与えています）。 

また このプログラム例では、θ(t) については、Solverを使わず、イールドカーブから解析的に求めています。この場合、３項Treeのように離散時間での確率過程をモデル化すると、誤差が発生する事が指摘されています。（Brigo-Mercurio ”Interest Rate Models-Theory and Practice” 2nd Edition, Springer, page80　参照）　 

 

<ライセンス表示>

QuantLibのソースコードを使う場合は、ライセンス表示とDisclaimerの表示が義務付けられているので、添付します。   ライセンス