1. QuantLibを使ってみる
1.2 Example を試す
1.2.6 BermudanOption プロジェクト (続き)
1.2.6.4 ソースコードの解析
では、ソースコードをステップ毎に説明します。ソースコードを見ながら読み進めて下さい。
1.2.6.4.1 事前準備 : Calibration 用のデータ および Calibration 実行と画面出力用の関数の定義
main()関数の前に、Calibration で使われる市場データと、Calibration の実行と結果の画面出力を担うローカル関数を準備しています。
(1) Calibration用の市場データを用意(51~61行目)
ソースコードにある通り、プレインバニラのSwaptionの市場データを用意しています。行使期間は、1年~5年の5通り、対象スワップの期間も1年~5年の5通りで、合計5×5=25個のデータが用意されています。データは、スワップションのBlack-Implied Volatilityの形で用意されています。後でわかりますが、実際にCalibrationの対象として使われるデータは、この中の5つだけです。
(2) ローカル関数の定義(63~89行目):
Calibration の実行と、Calibration 結果の画面出力用の calibrateModel() というローカル関数を定義しています。この関数は、引数として、次の2つのオブジェクトを取ります。
- Calibrationの対象となる“ShortRateModel”オブジェクト
- Calibrationの目的関数を提供する“BlackCalibrationHelper”オブジェクトの配列
それらを使って、次のような動作を行います。
- QuantLib が用意しているSolverを生成
- そのSolverを使って、モデルオブジェクトの calibrate()を実行。この関数が実際に Calibration アルゴリズムを実行し、モデルパラメータを導出します。
- 導出されたモデルパラメータを画面出力
ここで使われている、ShortRateModel(のベースクラスであるCalibratedModel) と CalibrationHelper の機能については、別途 Appendix 1, Appendix 2で解説します。 ここから以下は、main()関数本体について解説します。
1.2.5.4.2 日付とイールドカーブの設定(97~107行目)
まず、本日の日付と時価評価基準日を設定しています。20年以上前の日付になっていますが、このプロジェクト例が、最初に作成された頃と推定されます。
次に、イールドカーブを生成しています(102~107行目)。ここでは、フォワード金利が5%でフラットなイールドカーブを生成しています。
1.2.6.4.3 スワップションの対象スワップの生成(109~154行目)
ここでは、スワップションの対象となる、フォワードスタートの金利スワップを3種類(At The Money, Out of The Money, In The Money)生成しています。金利スワップオブジェクトの部品の生成と、組み立て方法は、既に MulticurveBootstrappiung プロジェクト例の所で説明済なので、解説は省略します。
1.2.6.4.4 Calibration Helperオブジェクトの生成(156~186行目)
このプロジェクト例の肝である、CalibrationHelper オブジェクトを、部品から生成し、組み立てています。
まず、CalibrationHelper の配列を作り、この配列に、5個の CalibrationHelper オブジェクトを生成し、格納しています。ここで生成された Calibration 対象のスワップションは、行使日 × 対象スワップ期間が 1年×5年、2×4、3×3、4×2、5×1の5種類です。
CalibrationHelper オブジェクトは、ベンチマーク商品の価格を、対象モデルでの価格とベンチマークモデルでの価格の2種類計算する役割を負っています。従って、このオブジェクトは、1個の Instrument と2種類の PricingEngine を内包しているオブジェクトと看做せます。詳しくは、Appendix 1をご覧ください。
1.2.6.4.5 4 種類の Short Rate Model オブジェクトを生成(192~196行目)
ここでは、4 種類の Short Rate Model オブジェクトを生成しています。4 種類といっても Hull-White モデルだけは、2つ生成しているので、実質的には3種類です。Hull-White モデルを2つ生成しているのは、CalibrationHelperで使うヨーロピアン・スワップションの価格計算アルゴリズムで、2通りの方法(解析解の方法と、3項Treeの方法)を試す為です。
いずれのモデルも、(114行目で生成した)イールドカーブオブジェクトを引数として取り込んでいます。このイールドカーブに、モデルの中心回帰レベルパラメータとなる関数 θ(t) をフィットさせます。そのアルゴリズムは、モデルオブジェクトの中に内包されており、価格エンジンを呼び出す度に Calibration されます。
モデルが出来上がったので、次にそのパラメータのCalibrationを行います。
1.2.6.4.6 Calibration の実行(201~244行目)
以上で準備が出来たので、いよいよ Calibration の実行です。最初に G2++ モデル(201~212行目)から。
(1)Calibrationの準備
- まず、先ほど生成したモデルオブジェクト(変数名 modelG2)を使って、G2++モデルを使った価格エンジン(G2SwaptionEngine)を生成します。
- さらに、その価格エンジンを、各 SwaptionHelper オブジェクトに設定します。その SwaptionHelper オブジェクトは、swaptions[i] という名前の配列に5個格納されているので、それぞれに、価格エンジンを設定します。
以上の操作を行っているコードを抜き出します。202~203行目の、たった2行です。
for (i=0; i< swaptions.size(); i++)
swaptions[i]-> setPricingEngine(ext::make_shared< G2SwaptionEngine > (modelG2, 6.0, 16));
PricingEngine のコンストラクターに渡している引数で、6.0 と 16 という値は、価格計算で使われる数値積分の、積分範囲(±6標準偏差)と、積分区間の分割数(16区間)を設定しています。
(2)Calibrationの実行
そこから、ローカル関数の calibrateModel() (コードの63~89行目で定義されたものです。)を呼び出し、Calibration を実行します。この関数内で、ShortRateModelオブジェクトの calibrate() という関数が呼び出されます。実際のアルゴリズムは、この関数内で走っています。より詳しい説明は Appendix 2参照。
(3)コンソール画面出力
206~212行目で、Calibrationされたモデルパラメータを画面出力しています。
他のモデルも、同様のステップなので、説明は飛ばします。Calibration の計算結果は、プロジェクト実行後の画面出力にある通りです。
1.2.6.4.7 バーミュ-ダン・スワップションの生成と価格計算(249~356行目)
以上でモデルの準備が出来たので、いよいよバーミューダン・スワップションの価格計算です。ここでは、スワップションの対象となるスワップを、3種類用意し、それぞれについて、4種類のShort Rate Modelで価格計算を行っています。また、計算結果を Bloomberg の価格と比較しています。
ここでは、At the Money のスワップを対象としたバーミュ-ダン・スワップションの価格計算だけを説明します。ITM と OTM も、手続きは同じなので、説明は省略します。
(1) 対象スワップの生成(249~263行目)
- まず、スワップションの対象となるスワップを生成します。
- 次に、バーミューダン・スワップションの行使日の配列を生成しています。
- それらの部品を使って、263行目でバーミューダン・スワップションを生成しています。
(2) 価格の計算と画面出力(268~284行目)
4種類の Short Rate Models を使った7種類の価格エンジンで、バーミューダン・スワップションの価格計算を行い、計算結果を画面出力しています。(プロジェクト実行後のコンソール画面出力を参照)
これまでのプロジェクト例と同じく、商品オブジェクトに価格エンジンオブジェクトを設定し、商品オブジェクトからNPV()を呼び出せば、計算結果が出力されています。価格エンジンは、3項Treeを使ったものと、FDM(Finite Difference Method :有限差分法)を使ったものを、モデルごとに用意し、価格計算を行っています。バーミューダン・スワップションの場合、どのようなモデルを使っても価格を解析解で求める事が出来ないので、Tree構造あるいは有限差分法といった数値解を求めるテクニックを使う必要があります。
以上で、このプロジェクト例の解説を終えます。
< Appendix 1 : CalibrationHelper クラス>
モデルの Calibration とは、Cap や Swaption といったベンチマーク商品の集合に対して、
- 対象となるパラメトリックなオプションモデルでの価格と、
- ベンチマークモデル(金利オプションの場合はBlackモデル)の価格
との差の2乗和が最小になるような対象モデルのパラメータを探すアルゴリズムです。言い換えると、パラメトリックなモデルを使う際に、そのモデルで計算したオプション価格が、ベンチマーク商品の市場価格に、最もフィットするようなパラメータを求めるアルゴリズムです。
これを数式で示すと、下記式のようになります。
(注1:上記式の右辺で、オプションの価格差ではなく、(Black) Implied Volatilityの差を使ってCalibrationする方法もあります。むしろ、実務ではそちらの方が一般的です。)
(注2:主要先進国の金利が、超低金利あるいはマイナス金利が現実化した今、金利オプションのベンチマーク商品の価格計算で使われていたBlackモデルは、もはや使えなくなりました。従って、上式のBlackPriceについては、Shifted LognormalモデルあるいはBachelierモデルを使ったものになっています。)
このような関数 \(f({\bf benchmark prices}; a,b,…)\) を、最適化問題(Optimization Problem)と呼び、右辺の誤差の2乗和(最適化の対象)を、目的関数(Objective function,または Cost function)と呼んでいます。
この式の右辺における、個々のベンチマーク商品の価格誤差\((BlackPrice-ModelPrice)\)の計算をオブジェクトモデル化したのが CalibrationHelper クラスになります。既に本文中で述べましたが、このクラスは、ベンチマーク商品の価格を、Calibration が必要なモデルと、ベンチマークモデルの両方を使って計算するので、このクラスの中に1個の Instrument(商品オブジェクト)と2個の PricingEngine(価格エンジン)が合体している看做せます。
そして、この価格誤差をすべてのベンチマーク商品で合計したもの(上式のΣ)が目的関数になります。プログラム例の 164~186 行目で、CalibrationHelper の配列(変数名swaptions)を生成していますが、これがまさに目的関数になります。
CalibrationHelperクラスの階層構造は、下記のようになっています(QuantLib Reference Manual の CalibrationHelperクラスダイアグラムを抜粋)。
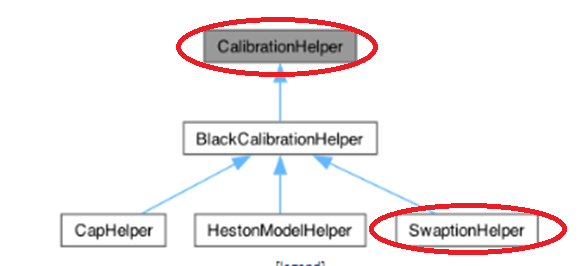
CalibrationHelper ベースクラスは抽象クラスで、そこから派生して、対象となるベンチマーク商品ごとに作られた具体クラスが、CapHelper、SwaptionHelper クラスになります。このプロジェクト例では、SwaptionHelper クラスが使われていますが、そこでは Swaptionオブジェクト(Instrument)の生成と、対象モデルとベンチマークモデルを使った2種類の価格エンジン(PricingEngine)の生成が行われ、さらに両者の価格差を計算するアルゴリズムが実装されています。
< Appendix 2 : CalibratedModel クラス >
さて、Appendix 1 で示した最適化問題を解くには、目的関数が最小になるようなパラメータを求めるアルゴリズムを走らせる必要があります。その最適化問題を解くアルゴリズムをオブジェクトモデル化したのが、CalibratedModel クラスになります。このクラスは、下記のダイアグラムにある通り、Calibration を必要とする様々なオプションモデルのベースクラスとなっており、Short Rate Model のグループも、このクラスから派生しています。 (QuantLib Reference Manualの CalibratedModel クラスダイアグラムを編集)。
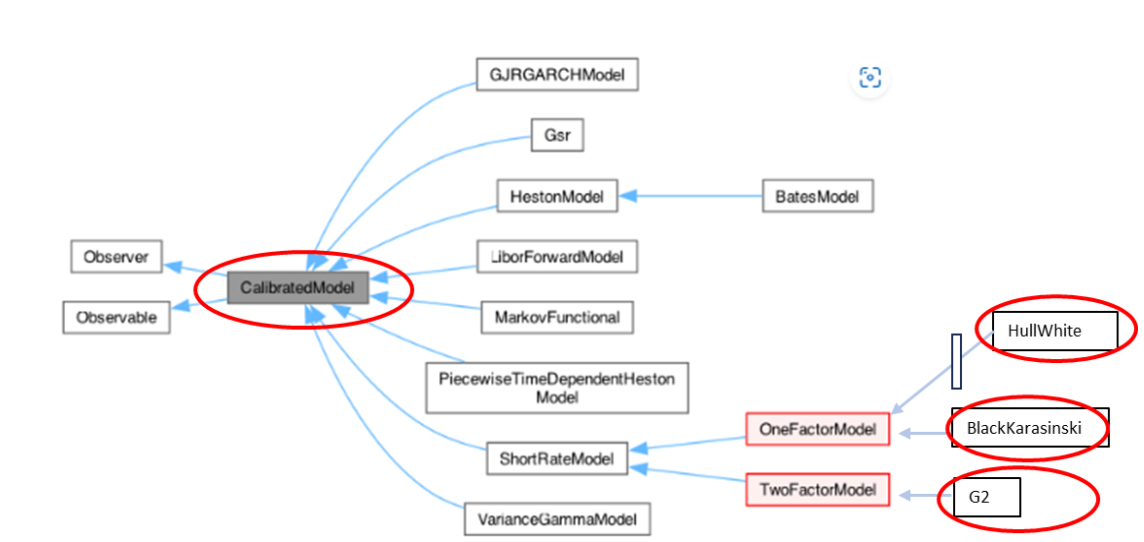
Calibration のアルゴリズムを走らせる為には、Solver や、制約条件・収束条件などの部品を必要とします。それらを列挙すると
- 目的関数(先ほど説明した SwaptionHelper オブジェクトの配列)
- 最適化問題を解く為の、多変数の Solver
- モデルパラメータの制約条件:例えば、Volatility パラメータであれば、その値は正でなければなりません。パラメータごとに、制約条件がある場合、その制約条件を付けた上でSolverを走らせなければなりません。
- Solverの終了条件 :Solverは、目的関数を繰り返し計算し、徐々に誤差を小さくしていきます。しかし、ほとんどの場合、誤差が 0 になる事は無いので、どこかで計算を終了する必要があります。その為に、何等かの終了条件を、設定する必要があります。
- ウェイト:誤差の値について、ベンチマーク商品ごとにウェイト付けする場合があります。ベンチマーク商品の中には、より流動性の高いAt the Moneyのオプションや、流動性の低いDeep out of the Moneyのオプションが含まれています。Calibrationを行う場合、流動性が高い(従って市場価格の信頼性がより高い)At the Moneyのオプションに、よりフィットさせたいと考えるのは、極めて合理的です。その為に、Calibration対象のベンチマーク商品に、一定のウェイトをつけてCalibrationする事があります。
以上のような、アルゴリズムや条件について、QunatLib はそれぞれオブジェクトモデル化した Class を提供しています。CalibratedModel クラスでは、calibrate() という関数が定義されており、この関数の引数として、上記で列挙した様々な部品を渡して、Calibration アルゴリズムが実行されます。参考として、この関数のインターフェースをソースコードから抜き出しました。
virtual void calibrate(
const std::vector <ext::shared_ptr<CalibrationHelper> >&, :目的関数
OptimizationMethod& method, :Solver
const EndCriteria& endCriteria, :終了条件
const Constraint& constraint = Constraint(), :制約条件
const std::vector<Real>& weights = std::vector<Real>(), :ウェイト
const std::vector<bool>& fixParameters = std::vector<bool>() :パラメータ
);引数の型をみればわかる通り、CalibrationHelper のほかに、OptimizationMethod、EndCriteria、Constraint といったクラスのオブジェクトが使われているのが分かります。
<ライセンス表示>
QuantLibのソースコードを使う場合は、ライセンス表示とDisclaimerの表示が義務付けられているので、添付します。 ライセンス