1. QuantLibを使ってみる
1.2 Example を試す
1.2.9 FittedBondCurve プロジェクト: 近似曲線を使った債券イールドカーブの構築
1.2.9.4 ソースコードの解析
1.2.9.4.1 フィッティング対象となる債券価格(イールド)の情報構築(83~159行目)
(1) まず、15 銘柄の債券価格を格納する配列(変数名 cleanPrice[] )を作成し、そこに債券価格を格納します。あくまでテスト用なので、とりあえず 15 銘柄すべて 100 に設定しています(83~88行目)。そして、そのデータを使って、Quote オブジェクト、さらにそのポインタを格納する RelinkableHandle< Quote > オブジェクトを作成します(95~98行目)。市場データを格納する Quote クラスや Handle< >クラス(RelinkableHandeはその派生クラス)の役割は、既に 実践編 1.2.3. MulticurveBootstrapping プロジェクト Appendix 1 と 3の所で、解説済です。
(2) 次に、クーポン支払い回数や日数計算方法や休日の取り扱いなどの債券 Cash Flow に関する情報を特定し、各変数に格納します(100~110行目)。また、本日の日付、カーブの基準日、カレンダーや決済期間、といった市場に関する情報も設定します。
(3) (1),(2) の情報を部品として、BondHelper オブジェクトを作成します(129~159行目)。BondHelper は、BootstrapHelperの派生クラスで、商品と価格エンジンを一体化したようなクラスです。このクラスのオブジェクトは、“イールドカーブを使って評価した債券価格”を計算し、それと市場価格との誤差を計算する事で、最小値問題におけるコスト関数の役割を担います。これについても、既に実践編1.2.3.4 MulticurveBootstrapping プロジェクト Appendix 4 の所で、解説済です。
これで、イールドカーブオブジェクト構築に必要な基本情報(部品)が揃いました。
1.2.9.4.2 イールドカーブの近似曲線の構築
(1) ここから、いよいよFittingMethodオブジェクトによるイールドカーブ構築です。「はじめに」で簡単に説明した通り、パラメトリックな多項式を使って、近似曲線を描きます。そのパラメータを、Solverを使って(最小2乗法を使って)求めるので、まず、Solverの計算回数の制約などの条件を設定します。その部分のコードを抜き出し、それぞれの意味を横に解説しています。
bool constrainAtZero = true; :T=0 時の Discount Factor の値を 1 に制約
Real tolerance = 1.0e-10; :最小値問題の許容誤差
Size max = 5000; :Solverの再帰計算の回数制限 最大5000 (2) まず、Bootstrapping-Interpolation法でイールドカーブを構築
166 行目で、PiecewiseYieldCurve< Discount, LogLinear> オブジェクトを生成しています。このイールドカーブは、Bootstrapping+Interpolation 法で生成されるもので、これも既に 実践編1.2.3 MulticurveBootstrappingプロジェクト の中で解説済です。
(3) さて、いよいよ7種類のFittingMethodによるイールドカーブを構築します。それぞれのオブジェクトの変数宣言とコンストラクターの引数を抜き出しました。、
ExponentialSplinesFitting exponentialSplines (constrainAtZero); (171行目)
SimplePolynomialFitting simplePolynomial (3, constrainAtZero); (184行目)
NelsonSiegelFitting nelsonSiegel; (197行目)
CubicBSplinesFitting cubicBSplines (knotVector, constrainAtZero);(221行目)
SvenssonFitting svensson; (233行目)
SpreadFittingMethod nelsonSiegelSpread (
ext::make_shared(),
discountCurve); (248行目)
ExponentialSplinesFitting exponentialSplinesFixed (constrainAtZero,7,0.02);(263行目) これらはすべて、FittedBondDiscountCurve::FittingMethod クラスの派生クラスで、このクラスは、FittedBondDiscountCurve クラスの内部クラスとして、このクラスのコンストラクターに、部品として渡されます。その一例として、ExponentialSplinesFitting クラスのコンストラクターを抜き出しました。5番目の引数が、FittingMethod オブジェクトになります。
auto ts1 = ext::make_shared< FittedBondDiscountCurve> (
curveSettlementDays, :本日から債券決済日までの営業日数
calendar, :カレンダー
instrumentsA, :BondHelperの配列。コスト関数を提供
dc, :日数計算方法
exponentialSplines, :FittingMethodオブジェクト
tolerance, :最小値問題の最小値許容範囲
max :Solverの再帰計算の制限回数
); この FittedBondDiscountCurve クラスと、その内部クラスである FittingMethod クラスと、さらにその派生クラスである、具体的な Fitting Method のクラスの役割と関係は、Appendix-1 と Appendix-2 で解説します。
(4) (3).で出来上がった7種類の FittedBondDiscountCurve の名前と、Solver の再帰計算回数の情報を、ローカル関数 printOutput()を使って、それぞれ Console 画面出力しています。(前出のConsole画面出力参照)
(5) (3).で出来上がった 7種類の discount curve から、ローカル関数 parRate()を使って、債券の Par Rate を導出し、Console 画面出力します。(275~337行目)
上記の(5)のステップについて、少し解説します。292~337行目にある for~loop の中で、各イールドカーブから、期間ごとの債券の Par Rate を導出し、画面出力しています。このfor~loopは、
for (Size i=0; i < instrumentsA.size(); i++) {にある通り、配列変数 instrumentsA の要素数だけ、計算を繰り返しますが、instrumentsA は、イールドカーブフィッティングの対象となった債券の情報を格納している BondHelper オブジェクトの配列です。そこから、債券のキャッシュフローの情報と満期日の情報を抜き出しています。
その上で、各イールドカーブを使って、各満期日に対応する債券の par Rate(債券価格が額面100%になるクーポンレート)を計算し、出力するようになっています。Par Rate を計算するアルゴリズムは、ローカル関数 parRate()で定義されています。画面出力にある通り、Bootstrapping-Interpolation 法で構築された par Rate も出力されており、それと比較する事で、イールドカーブのフィッティングの状況が分かります。但し、この例では、市場価格に対応するクーポンレートが 2 年ごとに、0.25%ずつ上昇する直線なので、曲線でフィッティングすると、どうしてもずれが発生します。FittingMethod の違いで、ずれの違いも出ていますが、ずれの程度で FittingMethod の優劣は判断できません。なので、この出力を判断基準にしないでください。
1.2.9.4.3 債券のデータを少し変えて同様の近似曲線を描く
前のセクションと同じ操作を、今度は債券のデータを動かして行っています。
(1) 債券決済日(bondSettlementDate)を23か月だけ先日付に動かして、全く同じ操作を行う。
(2) そこからさらに1か月先日付に動かして24か月先日付にすると、債券データの内、2年満期の債券は償還を迎えるので、フィッティング対象から消える。その上で、全く同じ動作を行う。
(3) 債券価格を若干動かす。当初はすべて100の設定であったが、各銘柄のイールドが5bp程度低下するように、債券価格を動かす。その上で全く同じ動作を行う。
以上の操作の結果は、前出のConsole画面出力の通りです。これにより、FittingMethodの優劣が比較できる訳では無いので、あまり意味のないテストであり、解説は控えます。
最後に、ここでは債券イールドカーブの近似曲線の描き方を何通りか紹介しました。しかし、これらの方法で描かれたイールドカーブは、あくまで(特定の発行体の)債券の利回りの期間構造の、全体としての雰囲気を知る程度の役割しか果たしません。なので、あまり厳密にカーブ形状を吟味しても意味は無く、ここで紹介した7種類の手法についても、その優劣にそんな差はありません。既に述べたように、Nelson Siegel や Svensson は、いくつかの中央銀行が、自国の国債市場のイールドカーブを把握するのに使っているようです。また、一部の大手証券会社のトレーディングデスクは、似たような手法で描かれたイールドカーブを使って、債券の割安・割高を判断して、アービトラージ取引(Convergence Trade)に使っているようです。
<Appendix - 1 : FittedBondDiscountCurveクラス>
本文中でも述べた通り、このクラスは近似曲線を使って Discount Curve を描く機能をカプセル化したクラスです。このクラス内部クラスである FittingMethod クラス(の派生クラス)の中で。具体的な近似曲線となるパラメトリックな多項式を定義し、多変数 Solver を使って、債券の市場データに最もフィットするようにパラメータを求めます。
FittingBondDiscountCurve クラスは、YieldTermStructure クラスの派生クラスで、YieldTermStructure クラスはさらに Termstructure クラスの派生クラスになります。この継承関係のダイアグラムを、QuantLibのReference Manual から抜き出しました。
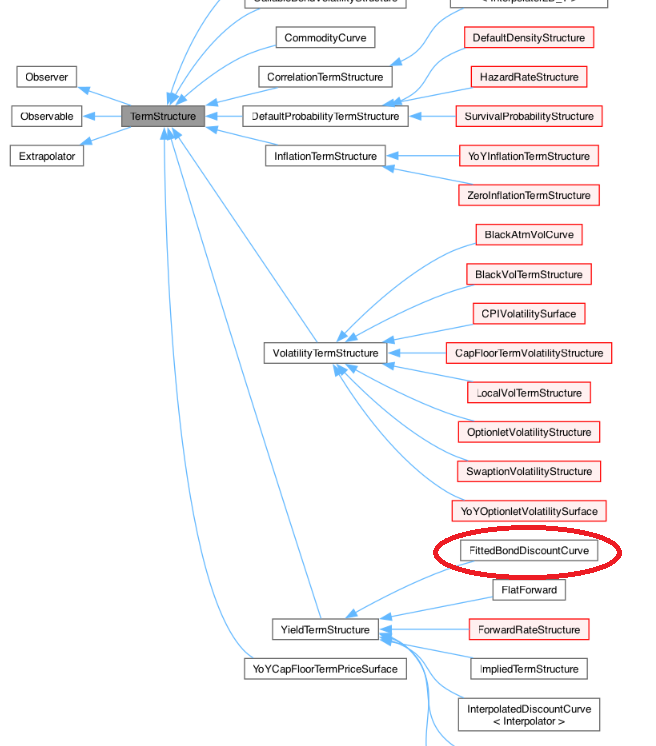
YieldTermStructure クラスから派生する他のクラスの大半は、Bootstrapping-Interpolation 法でイールドカーブを求めるのに対し、このクラスだけは、近似曲線を使ってイールドカーブを求めています。このクラスのオブジェクトを、どのような部品を使って組み立てるかを見る為に、コンストラクターのソースコードを抜き出しました。(本文中でも、その一例を示しています。)
FittedBondDiscountCurve::FittedBondDiscountCurve (
①コンストラクターの引数部分
Natural settlementDays, :債券の決済までの営業日数
const Calendar& calendar, :債券市場のカレンダー
vector<ext::shared_ptr<BondHelper>> bondHelpers,
:フィッティング対象となる債券のBondHelperの配列
const DayCounter& dayCounter, :日数計算方法
const FittingMethod& fittingMethod, :使われる近似曲線の種類
Real accuracy, :Solverの誤差許容範囲
Size maxEvaluations, :Solverの再計算回数の最大値
Array guess, :Solverに渡す初期推定値
Real simplexLambda, :SolverとしてSimplexを使う場合のλ値
Size maxStationaryStateIterations):Solverが平坦値を取ってからの再計算回数の最大値
②ベースクラスのコンストラクター呼び出し部分
: YieldTermStructure(settlementDays, calendar, dayCounter),
③引数をメンバー変数に格納する操作
accuracy_(accuracy),
maxEvaluations_(maxEvaluations),
simplexLambda_(simplexLambda),
maxStationaryStateIterations_(maxStationaryStateIterations),
guessSolution_(std::move(guess)),
bondHelpers_(std::move(bondHelpers)),
fittingMethod_(fittingMethod)
④コンストラクター起動時の動作設定
{ fittingMethod_->curve_ = this;
setup(); : ここではObserver(=this)をObservableオブジェクトへ登録
} まず、コンストラクターの引数ですが、イールドカーブを描く為に必要な最低限の情報(カレンダーや日数計算方法など)の他に、Solver に渡す制御変数をいくつか取っています。その後、引数の一部を使ってベースクラス(YieldTermStructureクラス)のコンストラクターを呼び出し、さらに残りの引数をメンバー変数に格納しています。SimplexLambda は、デフォールトの Solver として Simplex(downhill Simplex法または Nelder-Mead法)が使われている事から、そこで使う λ値(基底ベクトルにに掛ける乗数)になっています。
コンストラクターの中で、引数で取り込んだ FittingMethodオ ブジェクトを、自身のメンバー変数に取り込んだ後、setup()を呼び出しています。このsetup()は、自身をObserverとして、ObservableクラスであるBondHelperに登録する手続きを行っています。
<Appendix - 2 : FittingMethod クラス>
上記コンストラクターの引数の中で最も重要な部品は、FittingMethod クラスのオブジェクトです。FittingMethod クラスは、FittingBondDiscountCurve クラスの内部クラスとして宣言され、かつその Friend クラスになっています。このクラスは、近似曲線となる多項式(関数の線形結合)を格納するクラスで、その派生クラスで、具体的な関数形を特定します。このクラスの階層構造を QuantLib の Reference Manual から抜き出したものを下記します。
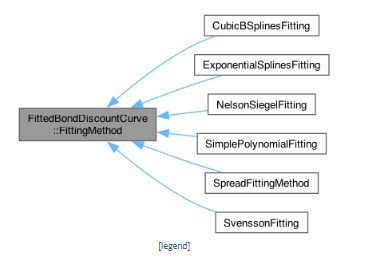
これらのクラスで定義されている近似曲線について、簡単に解説します。
① Cubic B-splines曲線 : discount curve を3次の B-Spline 曲線を繋ぎ合わせて描く。各 \(c_i\)(制御点列)に債券の Discount Factor を置き、それにフィットするように基底関数 \(N_{i,3}~(t)\) を決めていく。
\[ d(t) =\sum_{i=1}^n c_i*N_{i,3} (t), ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ \] \[\begin{eqnarray} 但し \\ & N_{i,0}(t)=\begin{cases} 1 & (t_i < t < t_{i+1}) \\ 0 & (otherwise) \end{cases} ~~~~~~~~~~~~~~~~~~~~~~~~~~\\ & N_{i,1}=N_{i,0}(t)\frac{t-t_i}{t_{i+1}-t_i} + N_{i+1,0}(t) \frac{t_{i+2}-t}{t_{i+2}-t_{i+1}} \\ & N_{i,2}=N_{i,1}(t)\frac{t-t_i}{t_{i+2}-t_i} + N_{i+1,1}(t) \frac{t_{i+3}-t}{t_{i+3}-t_{i+1} } \\ & N_{i,3}=N_{i,2}(t)\frac{t-t_i}{t_{i+4}-t_i} + N_{i+1,2}(t) \frac{t_{i+4}-t}{t_{i+4}-t_{i+1} } \end{eqnarray} \]その際、knot points となる \(t_i\) をあらかじめ決めておく必要がある。ソースコードでも、213 行目で 11個の knot points を外生的に与えている。Reference Manual によれば、カーブの形状は、この knots points の設定方法で大きく変わるので要注意とのこと。
1970年代に、ある文献で、この手法が紹介されました(McCulloch, J. 1971, "Measuring the Term Structure of Interest Rates.")。
② Exponential Splines : 指数関数の線形結合で曲線を表現。Merril Lynch が社内で使っていた方法を公開したもの。Discount curve を下記のような、9項からなる指数関数の線形結合で表現。\(c_i\) と \(κ_i\) が fitting parameter になり、債券利回りの市場データにフィットさせる。指数関数を9個も使っているので、かなり柔軟にカーブの形状が表現できますが、フィットさせるパラメータの数も多くなるので、Solverの計算時間も長くなってしまいます。(画面出力に Solver の再帰計算回数が出ていますが、この手法が圧倒的に回数が多くなっています。)
\[ d(t)=\sum_{i=1}^9 c_i* e^{κ_i~ t} \]③ Exponential Splines with fixed kappa : 上記の Exponential Splines で、\(κ_i\) を固定して使う方法。このプロジェクトでその方法もテストされている。カッパを固定する事で、パラメータの数を半分にし、再帰計算回数を減らして計算速度を向上できる。その分、カーブの表現力は劣る。
④ Nelson-Siegel : 基礎編 2.5.2 参照
⑤ Svensson : 基礎編 2.5.3 参照
⑥ Simple Polynomial : discount curve を下記式のような、n 次の多項式で表現し、各項の係数を fitting parameters として、債券の市場データにフィットさせる。 \[ d(t)=\sum_{i=0}^n c_i~ t^i \]
⑦ Spread Fitting: 使う場面がよく分からないので、解説は省略。
<ライセンス表示>
QuantLibのソースコードを使う場合は、ライセンス表示とDisclaimerの表示が義務付けられているので、添付します。 ライセンス