1. QuantLibを使ってみる
1.2 Example を試す
1.2.7 Gaussian1dModels : Gaussian Short Rate Model と Markov Functional Model
1.2.7.4 ソースコードの解析 (その2)
1.2.7.4.4 MaturityStrikeByDeltaGamma モードでの calibration と価格計算(279~323行目)
さて、CalibrationHelper の作成方法の2つめは、MaturityStrikeByDeltaGamma と呼ばれている方法です。この方法を使った、CalibrationHelper の生成と、Calibration の実行、価格計算の手順を見て行きます。
(1) calibrationBasket()関数を呼び出し、CalibrationHelper の配列を生成(289行目)
NonStandardSwaptionクラスのオブジェクト(変数名swaption)からcalibrationBasket()関数を呼び出し、CalibrationHelperの配列を生成します。
basket = swaption-> calibrationBasket(
swapBase, :スワップションの対象となるスワップ
*swaptionVol, :スワップションのVolatility Surface
BasketGeneratingEngine :: MaturityStrikeByDeltaGamma
);関数に渡している3番目の引数で、この方法を指定しています。
(2) 生成されたCaibrationHelperの配列を画面出力(294行目)
(3) 生成されたCaibrationHelper配列のそれぞれの要素に、価格エンジンを設定(306~307行目)
(4) GSRモデルからcalibrateVolatilitiesIterative()関数を呼び出してCalibrationを実行(310行目)
(5) Calibrationの結果を画面出力(313行目)
(6) バーミューダン・スワップションの価格評価 (319行目)
以上の手順で生成されたCalibrationHelperの配列と、CalibrationされたGSRモデルパラメータの画面出力を、下記に再掲します。また、バーミューダン・スワップションの価格も計算されており、76.27bpとなっています。
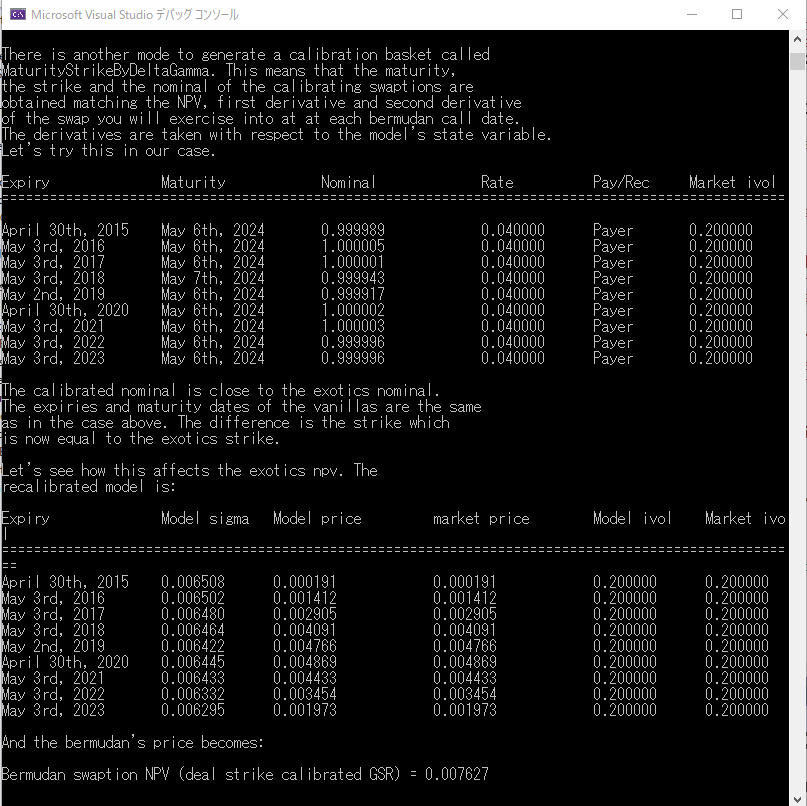
さて、生成された CalibrationHelper の配列と、それを使った Calibration 結果の画面出力について、2~3点、注意点を指摘しておきます。
- Naïveで生成されたCalibrationHelperはすべてAt The Money のスワップションを対象にしています。使われた
forecasting curveが、2.5%のフラットなカーブなので、ストライク金利は、すべて2.5%近辺になっています。(2.5%からの微妙なずれは、日数計算などによる微妙な差によるもの)
- Naïve での CalibrationHelper を使った calibration 結果は、Model による Implied Volatility と市場データの Implied Volatility が一致しています。
通常は、calibration 対象の市場データの数は、calibration されるモデルパラメータの数よりも多くなるので、完全に一致する事はありません。しかし、この例では、piecewise constantなσ(t)の数と、CalibrationHelperの数が同じなので、完全に一致しました。
- Calibration された σ(t) は、おおむね 0.5% 近辺になっています。この値は、ガウス分布における Volatility なので、金利の絶対水準の Volatility に相当します。それに対し、Market Implied Volatilityは、Black Volatility(対数正規分布のVolatility、すなわち変化率のVolatility)に相当し、それは20%で与えられていました。
- MaturityStrikeByDeltaGammaで生成されたCalibrationHelperは、ストライクがすべて4%になっています。このレートは、価格評価対象となるバーミューダン・スワップションのストライクレートと同じです。このように、この方法を取ると、CalibrationHelperは、対象商品のリスク属性に近いものが、自動的に生成されます。
- この方法で calibration された σ(t) は、おおむね0.63~0.65%になっています。市場の Implied Volatility は、ATMと同じ 20%ですが、ガウス分布と対数正規分布の差から、ストライクが異なると、導出されるガウス分布の Volatility は違ってきます。その結果、バーミューダン・スワップションの価格も、Naiveモードのケースと大きく異なっています。
1.2.7.4.5 元本逓減型のバーミューダン・スワップション (327~362行目)
次に、対象スワップの元本が逓減していく型のバーミューダン・スワップションの場合、どのようなCalibrationHelper が生成されるか見て行きます。ここでも、calibrationBasket()関数を、MaturityStrikeByDeltaGammaモードで 呼び出します。すると、元本逓減型の商品のリスク特性に近いようなCalibrationHelperの配列が生成されます。手順は以下の通りです。
(1) 元本逓減型のスワップを作成し、それを対象資産とするスワップションを作成(333~347行目)
対象スワップは、NonStandardSwapクラスのオブジェクト(変数名 underlying2)で、作成されたスワップションは、NonStandardSwaptionクラスのオブジェクト(変数名swaption2)になります。
(2) スワップションオブジェクトに、GSRを使った価格エンジンを設定(349行目)
(1) で作成されたスワップションオブジェクトに、221行目で生成した、GSRを使った価格エンジン(Gaussian1dNonstandardSwaptionEngineクラスのオブジェクト。変数名nonstandardSwaptionEngine)を設定
(3) calibrationBasket()関数を呼び出し、CalibrationHelper の配列を生成(352行目)
商品オブジェクト(変数名:nonstandardSwaption)から、calibrationBasket()関数を呼び出し、CalibrationHelperの配列を生成します(352行目)。この時、MaturityStrikeByDeltaGammaモードが使われています。
(4) 生成されたCalibrationHelperの配列を画面出力(357行目)
出力結果は、下記の通りです。ベンチマーク商品となるスワップションの対象スワップ満期日が全体的に少し短くなっています。また、みなし元本額も、オプション満期日が長くなるにつれ小さくなるように修正されています。これは、CalibrationHelperを、価格評価対象となる元本逓減型のスワップションのデルタとガンマに合わせた為です。
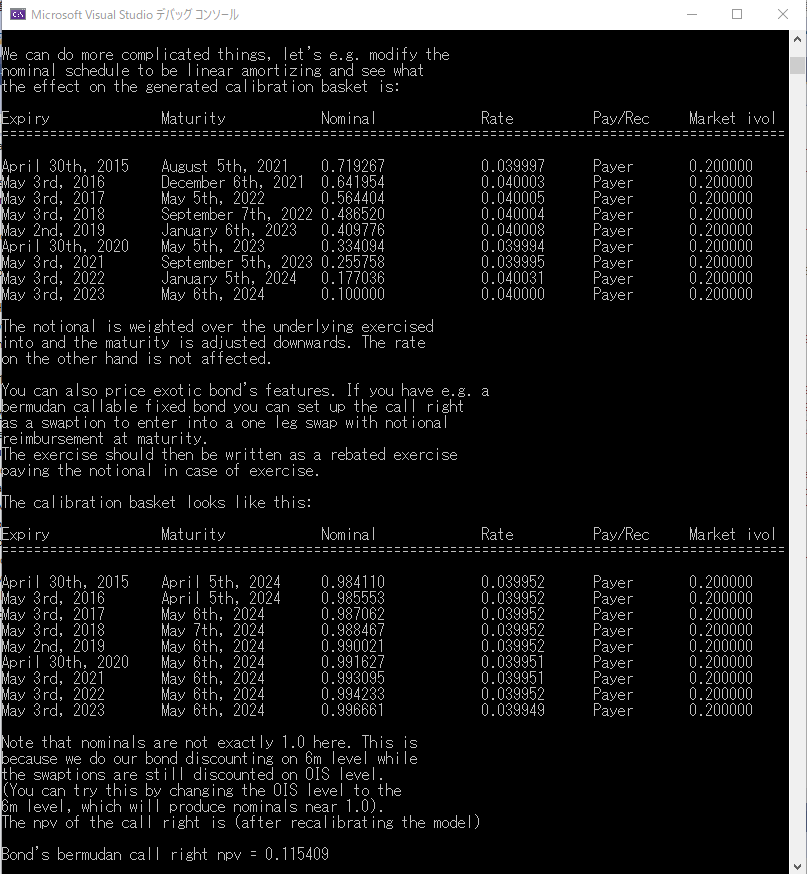
この部分はcalibrationBasket()関数の機能をテストする為だけなので、実際のCalibrationと価格評価は行っていません。
<ライセンス表示>
QuantLibのソースコードを使う場合は、ライセンス表示とDisclaimerの表示が義務付けられているので、添付します。 ライセンス