1. QuantLibを使ってみる
1.2 Example を試す
1.2.10 DescreteHeding : オプションデルタヘッジ戦略におけるヘッジエラーの検証
1.2.10.4 ソースコードの解析
1.2.10.1 ローカルクラスの定義(1):ReplicationPathPricerクラス
先ほど述べた通り、このプロジェクト内でしか使えないローカルクラスが2種類定義されています。コードで書かれている順番とは逆に、最初に ReplicationPathPricer クラスの内容から解説します。
このクラスは PathPricer クラスの派生クラスで、モンテカルロシミュレーションで生成された sample path 上で、Payoff などの計算を行うクラスです。QuantLib では、MonteCarloModel クラスが、モンテカルロシミュレーションのアルゴリズムを統括するクラスとして存在しています。このオブジェクトの主要部品として、価格経路を生成する PathGeneratorオブジェクトと、各経路上の Payoff を計算するPathPricerオブジェクトがあり、両者が協力してモンテカルロシミュレーションを実行します。このプロジェクトも、その枠組みを使っており、ReplicationError オブジェクトの中で、MonteCarloModel オブジェクトが作成され、その主要部品として、このReplicationPathPricer オブジェクトが使われています。MonteCarloModelクラスについては、Appendixでもう少し詳しく説明します。
さて、ReplicationPathPricer が行う経路ごとの Payoff 値などの計算は、operator()演算子(PathPricerベースクラスでは仮想関数として宣言されているもの)の中で実装されています。なので、実装された中味を見れば、このオブジェクトがやろうとしている事が分かります。その中味ですがソースコードの 200~285 行目を見てみます。
この演算子は、引数として Path クラスのオブジェクトを取ります。このオブジェクトは、PathGenerator オブジェクトによって生成された、個々の価格経路になります。この関数の実装を簡単にまとめると以下のようになっています。
Real ReplicationPathPricer::operator() (const Path& path) const {
(a) 202~218行目
Pathオブジェクトから、価格経路における価格観測点の数、
観測点の時間間隔、初期値(対象資産の現在価格)、等の情報を取得・設定。
(b) 224~236行目
ブラックモデルを使い、取引開始時における、オプションプレミアムの額、
及びデルタヘッジ額を計算し、それらの額を、変数“money_account”に代入。
ちなみに、この例では、callオプション売りを、対象資産のデルタロングでヘッジ
しているので、オプションプレミアム相当額の資金受取りと、デルタヘッジ購入に
必要な資金調達が発生します。
スタート時においては、両者合算では、資金調達額の方が大きくなるはずで、
当初のmoney_accountの額はマイナスになるはずです。
(c) 241~266行目
現時点からオプション行使日まで、価格経路上の価格観測点において、次の計算を行う。
i) b.で計算されたmoney_account額に対し、次の価格観測時点までに発生した
資金調達コスト(あるいは資金運用リターン)を計算し、
それをmoney_accountに加減する。
ii) 価格経路上の、次の価格観測時点の価格を基に、Blackの公式を使って、
価格変動後のデルタを計算。
iii) 新たに計算されたデルタで、デルタヘッジ額をリバランスする。
そのリバランスによって発生する追加の資金調達額(または資金運用額)を、
money_accountに加減する。
(d) 272~284行目
最終オプション期日における、経路上の対象資産価格を使い、
payoffを計算する。発生した損益相当額(callの売りなのでマイナスか0)を
money_accountに代入します。
また、その時点で残っていたデルタヘッジのポジションを処分し、
売却代金をmoney_accountに代入します。(デルタロングなので、売却代金は+)
その結果、money_accountの残高は、オプションのPayoffと、
それまで行ったデルタヘッジから発生した損益と、資金の調達コスト
(あるいは運用リターン)の総合計になっています。
}上記の(d)で計算された money_account の額は、価格経路の Volatility(経路上における価格変化率の分布の標準偏差)が、予想 Volatility(Black の価格公式で使った Volatility)と一致していれば、理論上はゼロになるはずです。しかし、モンテカルロシミュレーションで乱数を使って生成された個々の価格経路の実現 Volatility は、必ずしもそうなりません。その結果、sample path上の損益が0にならず、ヘッジエラー(誤差)が発生します。その誤差がどの程度になるかを計算するのが、次に説明する ReplicationError クラスになります。
1.2.10.4.2 ローカルクラスの定義 (2): ReplicationError クラス
このプロジェクトが行う実行内容の大半が、このクラスの中で実装されています。さらに言えば、このクラスのメンバー関数である compute() の中で実装されています(289~368行目)。もう一段突っ込めば、その compute() の中で作成された MonteCarloModel オブジェクトの中でアルゴリズムの大半が実行されています。前ののセクションのReplicationPathPricer::operator()も、MonteCarloModel の中で実行されています。なので、その中味を見れば、このクラスがやろうとしている事が分かります。
MonteCarloModel クラスは、QuantLib で提供されているモンテカルロシミュレーションのフレームワークの中で、最も重要なクラスのひとつです。QunatLib では、モンテカルロシミュレーションに必要な様々なアルゴリズムを、それぞれクラス階層でカプセル化しています。実際のモンテカルロシミュレーションは、それらを統合して行いますが、その統合されたクラスが、MonteCarloModel クラスになります。
このオブジェクトを使ったcompute()アルゴリズムの内容は、以下のようになっています。
- 対象資産の価格経路(sample paths)を生成する PathGenerator オブジェクトを作成し
- そこで生成された sample path ごとに ReplicationPathPricer オブジェクトを使って、オプションとデルタヘッジポジション全体のポジションから発生する全損益を計算し
- その結果を統計処理し、その全損益の分布に関する平均と標準偏差を計算する。
- 計算結果を画面出力する。
以上の動作の内、2. 3.は、compute()の中で生成された MonteCarloModel オブジェクトが行っています。
では、compute()の中味(289~368行目で実装)を見ながら、上記のアルゴリズムを少し掘り下げて見てみます。
(1) まず引数として、(i) シミュレーションで生成される、対象資産価格の離散的な価格過程(sample path)において、その価格の観測時点の回数(nTimeSteps) と、 (ii) 生成されるsample pathsの個数(nSamples)、を取ります(289行目)。
(2) PathGeneratorオブジェクトの生成(300~325行目)。
PathGeneratorオブジェクトは、確率過程モデル(ここではBlack Scholesモデル)を使って、対象資産価格が時間経過とともに拡散していく様子を、コンピューターシミュレーションで生成します。なので、まず確率過程モデル(ここではBlackScholesMertonProcess)オブジェクトを、その部品から作っていきます。300~310行目までで、その部品を用意し、311行目でそのオブジェクト(変数名diffusion)を作成しています。
またシミュレーションの為に乱数生成装置が必要ですが、それを、PseudoRandomクラス使って、317行目で作成しています(変数名rsg)。このクラスは、メルセンヌツイスターを使って一様乱数を発生させ、それを標準正規累積分布関数の逆関数を使って、標準正規乱数に変換するアルゴリズムを提供しています。
最後に、323 行目で、これらの部品を使って、PathGeneratorオ ブジェクトを作成します(変数名 myPathGenerator)。そのコンストラクターの引数を見れば、これがどのような部品から作られているかが分かります。
auto myPathGenerator = ext::make_shared<generator_type> (
diffusion, :価格過程オブジェクト
maturity_, :価格過程の最終期日(=オプション期日)
nTimeSteps, :最終期日までを離散時間で分割する数
rsg, :乱数生成装置
brownianBridge :ブラウンブリッジの使用可否
);(注:ブラウンブリッジは、2つの時点の確率変数が分かっている場合に、その中間点の確率変数を生成するテクニック。ここではfalseの設定なので、説明は省略します。)
(3) PathPricerオブジェクトの生成(330~332行目)
PathPricer の派生クラスである ReplicationPathPricer クラス(このプロジェクトのローカルクラス)のオブジェクトを生成しています。そのコンストラクターの引数を見れば、これがどのような部品から作られているかが分かります。それらの部品は、ReplicationError クラスの中のメンバー変数が使われています。
auto myPathPricer = ext::make_shared<ReplicationPathPricer> (
payoff_. :オプションのPayoff関数
optionType(), :オプションタイプ(Call or Put)
payoff_.strike(), :Payoffのストライク価格
r_, :リスクフリー金利
maturity_, :オプション行使日
sigma_ :Volatility
); これらの情報を使い、sample path 上の価格を使って、オプションの Payoff とデルタヘッジから発生する損益と、ポジションを構築するのに必要な資金調達コスト(or 資金運用リターン)の合計を計算します。
(4) Statisticsオブジェクトの作成(335行目)。
ここではQuantLibが用意した Statistics クラスのオブジェクトをそのまま作成しているだけです(変数名 statisticsAccumlator)。
(5) 以上の部品を使い、MonteCarloModelオブジェクトを作成(340行目、変数名MCSimulation)
さらに、このオブジェクトから、メンバー関数である addSamples()を呼び出し、具体的なモンテカルロシミュレーションが実行されます(347行目)。具体的には、引数であるnSamplesの数だけ、sample path が生成され、それぞれのsample pathで、ReplicationPathPricerにより、オプションとデルタヘッジから発生する損益が計算されます。
(6) 最後に、シミュレーション結果の統計値(平均、標準偏差、等々)を画面出力
以上が、ReplicationErrorクラスの説明ですが、ひとこと言わせてもらうと、このような動作内容を、あえてクラスとしてカプセル化する必要があるのかどうか、若干疑問です。すべてmain()関数の中で実装すればよく、あえて再利用の可能性が無いローカルなクラスにする必要性は感じません。
1.2.10.4.3 メイン関数本体(160~191行目)
最後に、main()関数の内容を解説します。ここでやろうとしている事は、
- シンプルなヨーロピアンタイプの call option を作成し、(期間1か月、ストライク100,対象資産価格100、volatility=20%、リスクフリー金利=5%)
- そのポジションとデルタヘッジポジションから発生する損益合計を、ReplicationError オブジェクトを使って、多数の sample path でシミュレーションし、
- シミュレーション結果(損益の期待値と標準偏差)を計算し、画面出力するという事です。
そのアルゴリズムの大半は、ReplicationError オブジェクトが担っており、171 行目でそのオブジェクトを作成(変数名rp)し、178 と 181 行目で、そおメンバー関数である compute()を呼び出してアルゴリズムを実行しています。アルゴリズムの内容は、既に解説した通りです。
最終的なシミュレーション結果は画面出力の通りですが、その内容について、若干解説します。画面出力を再度載せます。
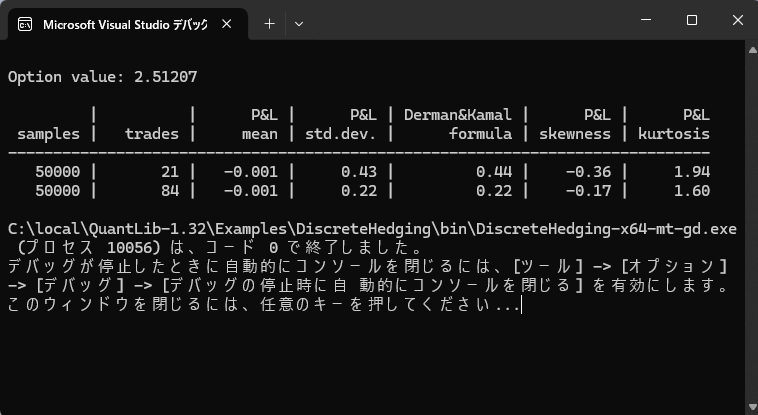
最初に、対象オプションの価格が出力されています。ここでは2.51207となっています。その下の表がシミュレーション結果になります。結果の上段は、オプション期日までにリバランスを 21 回行った場合、下段は、リバランスを 84 回行った場合になります。オプション期間が 1 か月なので、前者はおおむね1営業日ごとに1回のリバランス、後者は4回のリバランスを行っているイメージです。
サンプル総数 50,000 の平均損益はいずれも、-0.001 となっており、オプション価格との誤差は、約4bpポイントです。これは、デルタヘッジ戦略を何回も試行すれば、大数の法則により、オプション価値と Replicateされた取引戦略は、同じ価値に収束する事を意味します。
一方、損益の標準偏差は上段が 0.43(オプション価格の約 17%)、下段が 0.22(オプション価格の約 9%)になっています。つまり、オプション価値を Replicate する取引戦略は、かならずしもうまく行かない可能性があり、かつ、その精度はリバランスの回数が少ないほど悪くなります。逆に、リバランスの回数をどんどん増やして行けば、このシミュレーションによる誤差は0に収束していきます。Black Scholes モデルの前提は、デルタヘッジのリバランスを連続時間で無限回行えば、オプションのリスクを完全にヘッジできるというものですが、このシミュレーション結果は、それを示唆しています。
この誤差の発生原因は、モンテカルロシミュレーションで生成された sample path 上の価格変化が、path によっては、予想 Volatility と一致しない事から発生します。Sample path 上の対象資産価格は、Black Scholes モデルが予想する確率分布になるように、乱数を生成してつくられますが、sample path毎に見れば、乱数の性質上、必ずしも Black Scholes モデルが予想した volatility になりません。実際に発生した価格変動から計測された Volatility を実現 Volatility と呼びますが、それが予想 Volatility からずれた度合いだけ、損益もずれる事になります。言い換えると、生成された sample path上の価格分布の Volatility が、予想 Volatility と一致していれば、対象資産価格の path がどこに到達しても、最終的に損益合計は、ほぼ 0 になります。
出力にある Derman & Kamal formula は、シミュレーションで発生する損益の分布の標準偏差を、解析的に求める式で(「はじめに」で紹介した Goldman Sachs のリサーチレポート参照)、実際の標準偏差の値とほぼ一致しているのが分かります。
最後の2つのコラムにあるskewnessとkurtosis は、それぞれ歪度、尖度と呼ばれています。歪度は、確率分布における3次のモーメント、尖度は4次のモーメントに相当します。正規分布であれば、それぞれ0、3に収束するはずですが、それよりは若干ずれています。これは、Black Scholesモデルで生成された価格の確率分布は、正規分布ではなく対数正規分布なので、ずれが発生しています。
< Appendix : MonteCarloModel クラス >
MonteCarloModel クラスは、モンテカルロシミュレーションに必要な様々なアルゴリズムを組み合わせ、統合したクラスになります。その様々なアルゴリズムは、それぞれクラス構造でカプセル化されており、MonteCarloModel は、それらのオブジェクトを引数として取り、その中でアルゴリズムが統合されます。
デリバティブズの価格計算の中で使われるモンテカルロシミュレーションは、
- まず価格モデルが想定した確率過程に従う価格経路(sample path)を、乱数を使って生成し、
- 次にその価格経路上で、オプションのPayoff値を計算し、
- さらに、そのようなsample paths を多数発生させ、それぞれのPayoff値を計算し、
- 最後に、その平均を計算して、それをデリバティブズの価格と看做す
というアルゴリズムになります。
MonteCarloModel のメンバー関数である addSamples()の中で、1.2.3.を担うオブジェクトを使ってアルゴリズムを走らせ、sampleAccumulator() の中で4.を担うオブジェクトを使って計算を行います。
1.のアルゴリズムは、path_generator_type (価格経路生成装置)というクラスが担っており、2.のアルゴリズムは path_pricer_type(経路上のpayoff計算装置)と呼ばれているクラスが担っています。いずれも、実際のクラスの正式名称ではなく、typedef を使って付けられた別名になります。実際のクラス型は、MonteCarloModel クラスのテンプレート引数から取り出します。これらのクラス型のオブジェクトが、addSamples() の中で呼び出され、1.2.3.のアルゴリズムが実行されます。4.のアルゴリズムは、Statistics クラスのオブジェクトが担っています。
MonteCarloModel クラスは、これらのアルゴリズムを統合したテンプレートクラスで、そのテンプレート引数として、上記の path_generator_type や path_pricer_type のクラス型を特定するクラスを指定します。
下記に、QuantLib のソースコードから、このクラスの定義部分を抜き出しました。その構造は
- Template class名の宣言
{ - typedefを使い、テンプレート引数からクラス名の別名を作成
- コンストラクター
- メンバー関数の宣言
- メンバー変数の宣言
}
となっています。それぞれのパートについてコードの後で解説します。
template <template <class> class MC, class RNG, class S = Statistics>
class MonteCarloModel {
public:
typedef MC<RNG> mc_traits;
typedef RNG rng_traits;
typedef typename MC<RNG>::path_generator_type path_generator_type;
typedef typename MC<RNG>::path_pricer_type path_pricer_type;
typedef typename path_generator_type::sample_type sample_type;
typedef typename path_pricer_type::result_type result_type;
typedef S stats_type;
// constructor
MonteCarloModel (
ext::shared_ptr<path_generator_type> pathGenerator,
ext::shared_ptr<path_pricer_type> pathPricer,
stats_type sampleAccumulator,
bool antitheticVariate,
ext::shared_ptr<path_pricer_type> cvPathPricer
=ext::shared_ptr<path_pricer_type>(),
result_type cvOptionValue = result_type(),
ext::shared_ptr<path_generator_type> cvPathGenerator
=ext::shared_ptr<path_generator_type>()
)
: pathGenerator_(std::move(pathGenerator)), pathPricer_(std::move(pathPricer)),
sampleAccumulator_(std::move(sampleAccumulator)), isAntitheticVariate_(antitheticVariate),
cvPathPricer_(std::move(cvPathPricer)),
cvOptionValue_(cvOptionValue), cvPathGenerator_(std::move(cvPathGenerator))
{
isControlVariate_ = static_cast<bool>(cvPathPricer_);
}
//member functions
void addSamples(Size samples);
const stats_type& sampleAccumulator() const;
private: //member variables
ext::shared_ptr<path_generator_type> pathGenerator_;
ext::shared_ptr<path_pricer_type> pathPricer_;
stats_type sampleAccumulator_;
bool isAntitheticVariate_;
ext::shared_ptr<path_pricer_type> cvPathPricer_;
result_type cvOptionValue_;
bool isControlVariate_;
ext::shared_ptr<path_generator_type> cvPathGenerator_;
}; (1) template class
MonteCarloModelクラスは、冒頭のクラスの宣言文を見れば判る通り、3種類のtemplate引数を指定した template classになります。その3種類のTemplate引数は、
template< class> MC,
class RNG,
class S=Statisticsとなっています。
最初のテンプレート引数 “MC” は、それ自体も template class になっており、MC<RNG>という形のクラスを引数として指定する必要があります。なおかつ、MCのテンプレート引数は、2番目の引数 “RNG” で指定されたクラスになります。この形の template class として、QuantLibは、SingleVariate< RNG> と、MultiVariate< RNG> を用意しています。それぞれ指定された確率過程(1 factorモデルの場合は前者、multi-factorモデルの場合は後者)に従い、sample pathを生成するPath Generatorと、pathごとにpayoffを計算するPath Pricerのクラスを特定します。ちなみに、このプロジェクトではMC< RNG> としてSingleVariate< PseudoRandom> が使われており、そのクラス内で、PathPricer<Path>と、PathGenerator< PseudoRandom> というクラス型が特定されています。
2番目のテンプレート引数“RNG”は、乱数生成装置クラスが指定されます。このクラス内では、一様乱数を生成し、それを正規乱数に変換するアルゴリズムが実装されています。ちなみに本プロジェクト例では、PseudoRandom という名前のクラスが使われています。このクラスは、メルセンヌツイスターと呼ばれる一様乱数生成アルゴリズム(MersenneTwisterUniformRngクラス)を使い、それを、標準正規累積分布関数の逆関数(InverseCumulativeNormalクラス)を使って、標準正規乱数に変換するアルゴリズムが使われています。
最後のテンプレート引数 ”S” は、Statisticsクラスで、生成されたサンプルの値の平均や標準偏差などの統計値を計算します。Statisticsはデフォールト値として設定されたクラス名になります。
(2) typedefによる型指定
実は、上記の template 引数は、すべて構造体で、class ではありません。具体的なクラス名は、その構造体の中で、さらに typedef を使って指定されています。先ほど示した SingleVariate<PseudoRandom> という名前の構造体の中では、PathGenerator< > , PathPricer< > といったクラス名が、指定されています。そして、MonteCarloModel は、typedefを使って、これらの指定されたクラス名を使って、新たなクラス型名を宣言しています。(path_generator_type, path_pricer_type, stas_type など)。このように、テンプレート引数の型名として、特定のクラス名を使わず、そのクラス名を指定した構造体を使うテクニックは、 traitsと呼ばれています。オブジェクト指向のプログラミング技術の中でも難解な方法のひとつであり、ここではその解説をしませんが、Webで検索すれば、参考となる情報は多数出てくると思いますので、そちらを参照して下さい。
また、Luigi Ballabio 氏の “Implementing QuantLib” の、Monte Carlo Framework の解説の中で、この traits の使い方の解説が為されています。該当箇所の日本語訳はこちら Monte Carlo traits
(3) コンストラクター
コンストラクターは、テンプレート引数で指定されたクラスから、具体的な PathGenerator や PathPricer、GenericRiskStatistics のオブジェクトを引数として取り、これらを、メンバー変数に格納します。
(4) メンバー関数: addSamples()
この関数の中で、PathGenerator を使って sample path を生成し、PathPricer を使って、sample path 上の Payoff を計算し、それを指定されたサンプル数まで実行し、計算結果を、sampleAccumlator_(Statisticクラスのオブジェクト)に渡します。
(5) メンバー変数
PathGeneratorやPathPricerや、Statisticsクラスのオブジェクトが格納されます。
QuantLib が用意しているモンテカルロシミュレーションのフレームワークは、巨大で、様々なクラス群で構成されていますが、それらのクラス群を統合するのが MonteCarloModel クラスになります。さらに、MonteCarloModel クラスを使って、様々な金融商品や、様々なモデルに対応した価格エンジンが、ライブラリとして用意されています。このフレームワーク全体については、Ruigi Ballabio氏の“Implementing QuantLib”の中で詳細に解説されていますので、それも参考にして下さい。また、その日本語訳は、本サイトの実践編 2.6 Monte Carlo Frameworkに載せています。
また、オプション価格の計算に使われるモンテカルロシミュレーションの様々なテクニックについては、上級編 6.6 モンテカルロシミュレーション で解説しています。
<ライセンス表示>
QuantLibのソースコードを使う場合は、ライセンス表示とDisclaimerの表示が義務付けられているので、添付します。 ライセンス