1. QuantLibを使ってみる
1.2 Example を試す
1.2.10 DescreteHeding : オプションデルタヘッジ戦略におけるヘッジエラーの検証
1.2.10.1 はじめに
このプロジェクトは、Goldman Sachsの株式リサーチレポート “When you cannot hedge continuously”で紹介されていた、オプションのデルタヘッジ戦略から発生するReplication Error値を、コンピューター上のシミュレーションで検証したものです。
そもそも、Black Scholes から始まるオプション価格理論は、「オプションのリスクを完全にReplicate(複製)出来る取引戦略が存在する」 という考えが前提になっています。その様な取引戦略でヘッジされたオプションのポジションはリスクが完全に消され、リスクフリーとなるので、そこから利益を上げる事はできません(正確には、当初の全体ポジション額をリスクフリー金利で運用したリターンしか得られず、そのポジション額をリスクフリー金利で調達すれば、ネット損益は 0 になる)。
そこで仮定されている「リスクを完全にReplicate出来る取引戦略」とは、対象資産価格の変動に合わせて、連続時間で、デルタヘッジのリバランスを、無限回行う、というものでした。これは、現実的には不可能ですが、実務では、有限回のリバランスを、そこそこの回数行えれば、それに近い効果が得られると考えられており、実際にオプションのトレーダーの多くは、その考え方をベースにオプションのヘッジを行っています。その際、何回くらいリバランスを行えば、リスクがどの程度消えるのかを検証したのが、今回のプロジェクトになります。このシミュレーションの結果、リバランスの回数を増やせば、実際にリスクは小さくなるのですが、一方で取引コストも増大するので、適度なバランスが必要になります。
このプロジェクトでシミュレーションされている内容は、下記のようなものです。
1.ヨーロピアンのコールオプションの売りポジションを、Black Scholesモデルで計算されたデルタを使って、対象資産の買いでヘッジする。
2.モンテカルロシミュレーションで、Black Scholesモデルに従った、対象資産価格の価格過程(sample path)を生成する、その際、オプション期間を離散時間で分割し、各時点の価格と残存オプション期間に応じてデルタを再計算し、ヘッジをリバランスする。このリバランスを、オプション期日まで、有限回繰り返す。(21回と84回の2通りのパターンで検証)
3. sample pathがオプション最終期日に到達した時点の価格で、
+ payoff額と、
+ オプション期日までに行ったデルタヘッジから発生した売買損益の合計と
+ ポジション構築にかかった資金(オプションプレミアムの受取りと
デルタヘッジに必要な資金調達)の資金調達コスト・資金運用リターンの合計を
計算し、それらを合算する。
4.この操作を50000通りのsample pathで行う。
5.その結果得られた損益の分布について、平均と標準偏差等の統計値を求め、画面出力する。
この損益分布の平均は、理論上 0 になるはずで、実際のシミュレーションでも、ほぼそうなっています。しかし、個々の sample path 上の損益は、必ずしも 0 にならず、損益は一定の散らばりを見せます。これは、シミュレーションで、生成された個々の sample path 上の価格変化率の標準偏差(実現Volatility)が、必ずしも Black Scholes モデルで想定された Volatility(予想Volatility) と一致しないからです。実際に、実務でオプションのデルタヘッジ戦略を取った場合も、実現 Volatility が予想 Volatility と異なる事によって、ヘッジのエラーが発生します。
このプロジェクトは、そのエラーが、どの程度の大きさになるかを、コンピューター上のシミュレーションで計測しようとするものです。
このプロジェクトでは、モンテカルロシミュレーションを、QuantLib が用意しているクラス群を使って行っています。モンテカルロシミュレーションは、様々な乱数の生成方法、商品ごとに異なる Payoff の計算方法、分散逓減の為の様々なテクニック、などを組み合わせて行います。QuantLib では、それらの選択肢をクラスでカプセル化し、Template Class を使ってうまく組み合わせる事によって、簡単にモンテカルロシミュレーションが行える様なクラスライブラリーが提供されています。
これまでのプロジェクト例が、金融商品と価格エンジンのオブジェクトを部品からどう作っていくかに焦点をあてて解説してきましたが、このプロジェクトでは、QuantLib が提供しているモンテカルロシミュレーションの枠組みが、どのようなもので、どうやって使うかを中心に解説したいと思います。
1.2.10.2 プロジェクトのビルド
これまでのプロジェクトと同様、まず ”DiscreteHedging” プロジェクトのソースコードをビルドします。
- QuantLib のディレクトリ下にあるソリューションファイル "QuantLib.sln" を開けます。すると、Visual Studio が起動され、このソリューションファイル下にあるプロジェクトがオープンされます。ソリューションエクスプローラー画面にある 21 個のプロジェクトファイルの中から、DiscreteHedging プロジェクトを選択します。
- DiscreteHedging プロジェクトのディレクトリを展開し、SourceFiles のフォルダーにある "DiscreteHedging.cpp" をクリックすると、約 370行あるソースコードが開かれます。
- メニューバーから “プロジェクト(P)” → “スタートアッププロジェクトに設定(A)” を選択します。これで、QuantLib.sln の中で、最初に DiscreteHedging プロジェクトのメイン関数が呼び出されます。
- 同じくメニューバーから、 “プロジェクト(P)” → “プロパティ(P)” を選択し、これまでのプロジェクトと同様、boost ライブラリへのパスを設定します。(実践編1.1.5 “QuantLibソリューションのビルド”の解説を参照)
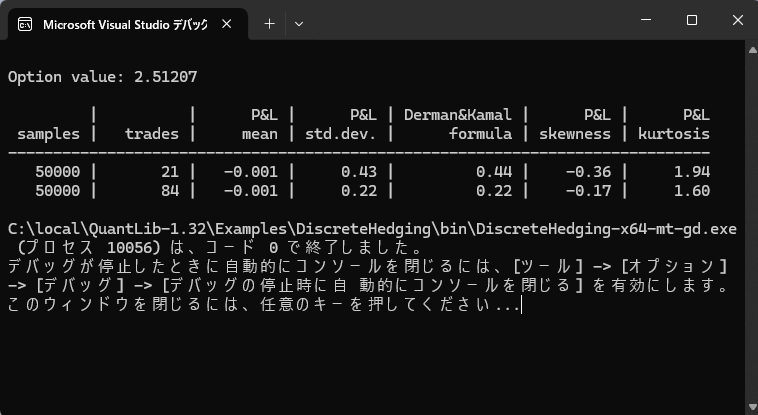
- メニューバーから "ビルド" → "DiscreteHedging のビルド" を選択するとビルドが開始されます。エラー無くビルドが正常終了すれば、試しにプログラムを走らせてみます。メニューバーの "デバック" → "デバックの開始" を選択し、下記のConsole画面が出力されれば成功です。
(注:プログラムが終了すると同時にConsole画面も消えてしまうようであれば、"ツール" → "オプション" → "デバック" → "全般" とし、「デバックの停止時に自動的にコンソールを閉じる」 のチェックボックスをオフにする。)
1.2.10.3 ソースコードの全体像
このプロジェクトのソースコードは、 DiscreteHedging.cpp になります。この解説はそのソースコードを見ながら読み進めてください。それをブラウザーでも見れるように、htmlファイルに変換したソースコード"DiscreteHedging.cpp"を載せておきます
さて、ソースコードは見ての通り、約370行あり、その構成は、下記のようになっています。
| ― | プリプロセッサー | (1~64行目) |
| ― | ローカルクラスの定義 | (70~156行目) |
| ― | メイン関数 | (160~191行目) |
| ・ 本体 | (162~183行目 try{}で囲まれた部分) | |
| ・ 例外処理 | (184~190 catch{}部分) | |
| ― | ローカルクラスのメンバー関数の実装 | (200~368行目) |
この内、ローカルクラスですが、このプロジェクト専用に作られた2種類のクラスがあります。それぞれのクラス名と役割は次の用になっています。
| ・ ReplicationErrorクラス | まず、検証対象となるヨーロピアンコールオプションを作成する。次に、MonteCarloModelクラスのオブジェクトを使って、そのオプションとデルタヘッジの合算ポジションから発生する損益を、モンテカルロシミュレーションで生成された50000通りのサンプルを使って計算。さらに、その損益の、平均と分散を計算し、それを画面出力する。 |
| ・ ReplicationPathPricerクラス | QuantLibで用意されているMonte Carloシミュレーションの機能を使い生成された価格経路ごとに、 ① Payoff損益と、 ② デルタヘッジから発生する損益と、 ③ ポジション全体にかかる資金調達コスト(あるいは運用リターン) を合計します。このオブジェクトは、上記の ReplicationError オブジェクトの中で生成された MonteCarloModel オブジェクトに渡され、シミュレーションに使われます。 |
上記2つのクラスが実行する主要なアルゴリズムは、それぞれの下記のメンバー関数の中で記述されており、その実装は 200行目以降で行われています。
| 200~285行目 | ReplicationPathPricer::operator() | sample pathごとに、オプションPayoffとデルタヘッジと、資金調達コスト(or 運用リターン)の合計を計算。 |
| 289~368行目 | ReplicationError::compute() | MonteCarloModelオブジェクトを使って、50000通りのsample pathから、上記operator()で計算された損益合計の平均と分散を計算し、画面出力する。 |
メイン関数の本体部分は、上記の ReplicationError オプジェクトを生成し、そこから compute() を呼び出して、アルゴリズムを走らせるだけです。
上記の説明の中で、MonteCarloModelオブジェクトが何度か使われています。これは、QuantLibが用意しているモンテカルロシミュレーションのフレームワークを提供している重要なクラスです。その内容については、Appendixを参照して下さい。
この全体像を踏まえながら、次にソースコードの中味を解説していきます。
<ライセンス表示>
QuantLibのソースコードを使う場合は、ライセンス表示とDisclaimerの表示が義務付けられているので、添付します。 ライセンス