1. QuantLibを使ってみる
1.2 Example を試す
1.2.7 Gaussian1dModels : Gaussian Short Rate Model と Markov Functional Model
1.2.7.4 ソースコードの解析 (その4)
1.2.7.4.7 Constant Maturity Swapを対象としたスワップションの価格評価(1)
さて、次にConstant Maturity Swapと、それを対象資産とするバーミューダン・スワップションの価格評価を見て行きます。Constant Maturity Swap(以下“CMS”)とは、
・IBOR(LIBORやEURIBORなど)にリンクする変動金利キャッシュフロー(”IBOR-CF”) と
・特定の期間(例えば10年物)のスワップ(CMS)金利にリンクする変動金利キャッシュフロー(”CMS-CF”)
を交換する金利スワップになります。
CMS-CFの方は、金利発生期間(3か月とか6か月)と変動金利インデックスとなるスワップ金利の期間(10年とか20年)が一致しません。順イールドカーブの傾斜がきついと、CMS-CF の方が、受け取り額が大きくなるので、カーブの傾斜がきつくなる方向を狙った商品になります。イールドカーブが順イールドだった2000年代前半くらいまで、よく取引されていました。しかし、その後の金融危機で、主要先進国の金利が軒並み超低金利でイールドカーブがフラットになっていった為、商品としての魅力が無くなり、今では殆ど取引されていないと思います。
(注:IBORサイドの変動金利インデックスは、LIBORが廃止されており、新規にこのインデックスを使った取引はありません)
CMSの価格評価は、IBOR-CFの方はシンプルですが、CMS-CFの方は、コンベクシティ―調整が必要になります。なので、調整額を計算するのにオプションモデルが必要になります。
ここでは、 以下のようなテストが行われています。
- CMS スワップの商品オブジェクトを作成し、次に、それを対象資産とする CMS スワップションオブジェクトを作成。
- Gaussian1dFloatFloatdSwaptionEngineオブジェクトを作成し、上記の CMS スワップションオブジェクトに設定
(この価格エンジンについては、Appendix-1で解説) - まず対象資産となる CMS スワップの価格評価を、簡便な Linear TSR Model を使って計算。
(Linear TSRモデルについては、Appendix-3で解説) - CMSスワップション用のCalibrationHelperを生成し、GSRモデルのCalibrationの実行
- GSRモデルを使って、CMSスワップションの価格計算
- GSRモデルを使って、CMSそのものの価格計算
まず、この手順を見て行きます。
(1) まず CMS スワップの商品オブジェクト(FloatFloatSwapクラスのオブジェクト)を作成(469~472行目)
商品オブジェクトの作成は、これまで通り、事前に作成した部品を、商品オブジェクトのコンストラクターに渡して組み立てます。下記に469行目にある FoatFloatSwapのコンストラクターを抜粋し、どのような引数(部品)が使われているか示しています。大半の部品は、既に作成済みなので、それを使っています。少し複雑な商品なので、組み立てに必要な部品も多数揃える必要があります。
auto underlying4 = ext::make_shared <FloatFloatSwap>(
Swap::Payer, :スワップのタイプ、IBORの反対側のCFがPayer
1.0, :みなし元本1、
1.0, :みなし元本2
fixedSchedule, :Payer側(CMS-CF)のキャッシュフロースケジュール
swapBase, :Payer側(CMS-CF)の変動金利インデックス。
Thirty360(Thirty360::BondBasis), :Payer側のCFの日数計算方法
floatingSchedule, :Receiver側(IBOR-CF)のスケジュール
euribor6m, :IBOR側の変動金利インデックス
Actual360(), :IBOR側の日数計算方法
false, :途中での看做し元本の交換:無しに設定
false, :最終期日でのみなし元本の交換:なし
1.0, :Payer側キャッシュフローごギアリング
0.0, :Payer側キャッシュフローのスプレッド
Null(), :IBOR側のCAP:無しに設定
Null(), :IBOR側のFloor:無しに設定
1.0, :IBOR側のギアリング
0.0010 :IBOR側のスプレッド:0.1%に設定
); (2) (1),を対象資産とするバーミューダン・スワップションの商品オブジェクトを作成(474行目)
ここでは FloatFloatSwaptionクラスのオブジェクトを作成しています。
(3) 価格エンジンの生成(476行目)
ここでは、BasketGeneratingEngine クラスの派生クラスである Gaussian1dFloatFloatSwaptionEngine クラスのオブジェクトを作成しています。(Appendix-1参照)
(4) 商品オブジェクトに価格エンジンを設定(479行目)
以上で価格計算の準備が出来ました。
(5) CMS 自体の価格評価を、Linear TSRモデルを使って行う(481~510行目)
CMS スワップションの価格評価の前に、まず対象資産となる CMS 自体の価格評価を、Linear TSRモデル(LinearTsrPricerクラスのオブジェクト)を使って行います。(Linear TSRモデル(線形ターミナルスワップ金利モデル)については、Appendix-3で、簡単に解説)
QuantLib では、変動金利 CF の価格評価を、クーポン毎に FloatingRateCouponPricer (クーポン専用の価格エンジン)を設定して計算しています。これについては、既に Bondsプロジェクトの解説のAppendix-5で説明しました。CMSスワップの場合、IBOR側のクーポンCFと、CMS側のクーポンCFに、それぞれのCFに対応したFloatingRateCouponPricerのオブジェクトを設定し、価格計算を行います。 ここでは、以下のように、2種類のCouponPricerを使っています。
- 491行目で LinearTsrPricer(FloatingRateCouponPricer の派生クラス)オブジェクトを生成し、494行目で、それを CMS 側のクーポンに設定。
- 492行目で BlackIborCouponPricer(これも FloatingRateCouponPricerの派生クラス)オブジェクトを生成し、495行目で、それを IBOR 側のクーポンに設定
前者は、各CMSキャッシュフローの Convexity Adjustment を行い、後者は、単にフォワード IBOR 金利の CF を生成するだけです。
そして、それぞれの CF を現在価値に換算する為、DiscountingSwapEngineオブジェクトを作成し、それを使ってCMSスワップの価格評価を行っています。(502行目)
さらに、ここから、CMSスワップを対象としたバーミューダン・スワップションの価格評価を行っていきます。
(6) CMSスワップション用に、CalibrationHelperを生成し、GSRモデルのCalibrationを実行(518~526行目)
次に、CMS スワップを対象資産としたバーミューダン・スワップションの価格評価を行いますが、その為には、まず CalibrationHelperを生成し、それを使ってモデルパラメータのCalibrationを行う必要があります。その手続きは、これまでと同様で、以下の通りです。
・CMS スワップションオブジェクトから、calibrationBasket()関数を呼び出し、この商品に対応した CalibrationHelper の生成。ただし、ここではNaiveモードで行っているので、必ずしもそうなっていません。(注:この設定をMaturityStrikeByDeltaGammaモードに変えて再ビルドしプログラムを走らせましたが、生成されたCalibrationHelperの看做し元本額が非常に小さな値で出てしまいました。おそらくこの関数は、CMSスワップには対応していないのでしょう。)
・ calibrateVolatilitiesIterarive()関数を使い、GSRモデルのパラメータのCalibrationの実行(522行目)
・ CalibrationHelper の配列と、Calibration の実行後のモデルパラメータを画面出力(525,526行目)
(7) GSRモデルを使って、CMSバーミューダン・スワップションの価格評価(532~536行目)
ここでは、Gaussian1dFloatFloatSwaptionEngine を使った価格計算を行っています。
(8) GSRモデルを使って、CMSスワップの価格評価(539~543行目)
ついでに、この価格エンジンを使って、スワップションの対象となったCMSスワップの価格評価を行い、LinearTSRモデルを使った場合と比較(539~543行目)
以上の計算結果の画面出力は、以下の通りです。
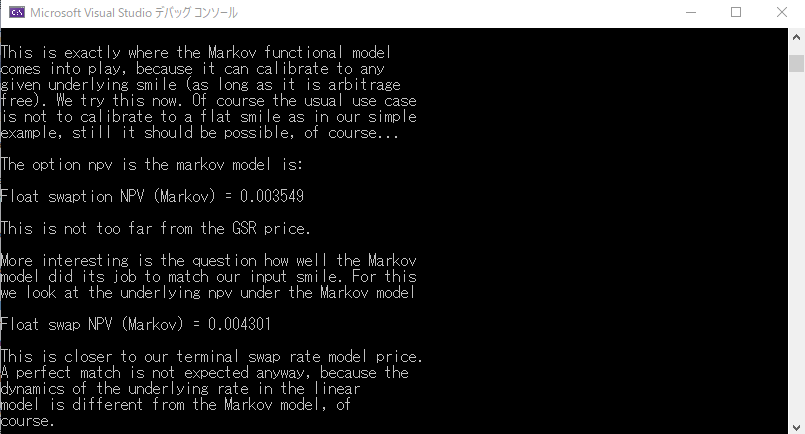
このアウトプットの最後にある、CMS自体の価格が52.5bpとなっています。Linear TSRモデルでの価格評価は、44.47bpだったので、約18%の差が発生しました。その理由は、アウトプットの最後のコメントにもある通り、Linear TSRモデルが想定しているVolatility Smileカーブと、GSRモデルが想定しているそれとが、異なっているからです。
それに対し、市場のスマイルカーブにもうまくフィットできる1ファクターモデルが、次で使うマルコフ汎関数モデルになります。
1.2.7.4.8 Constant Maturity Swapのスワップションの価格評価(2)
次に、CMS スワップションの価格評価を、Markov Functional Model(マルコフ汎関数モデル“MFM”)を使って行っています。MFM は、ニュメレールとなるゼロクーポン債の価格の確率過程をモデル化したもので、1990年代の後半に登場しました。1ファクターモデルにもかかわらず、市場の Volatility の期間構造と、Volatility Smile カーブにうまくフィット出来る事から、実務でも使われるようになりました。ただ、背景にある理論、考え方や、モデルを実装する為のアルゴリズムが非常に複雑で、理解は容易ではありません。ここでは、QuantLib が提供している MFM モデルの使い方と、それを使った価格エンジンで CMSスワップションの価格評価方法についてだけ、解説します。理論面については、上級編のマルコフ汎関数モデルのセクションをご覧ください。
ステップとしては、
- MFM オブジェクトの作成
- MFM モデルを部品に、Gaussian1dFloatFloatSwaptionEngineを作成
- CMS スワップションに、(2)の価格エンジンを設定
- スワップションの価格計算
- MFM の Volatility パラメータを、ATMスワップションの CalibrationHelper を使ってCalibrateし
- Calibration 後の MFM を使って、スワップションの対象資産である CMS 自体の価格計算
となっています。
では、以上の手順を、もう少し詳しく説明していきます。
(1) MFM オブジェクトを、部品から作成(557~565行目)
コードを見ての通り、557~561行目でMFMの部品をいくつか事前に作成し、それらを 562行目でMarkovFunctionalクラスのコンストラクターに渡しています。MarkovFunctionalクラスは、GSRと同様、Gaussian1dModelsクラスから派生したクラスです。QuantLibのReference Manualから、このクラスの部分のURLを添付します。
MarkovFunctional Class Reference
(2) (1),のMFMオ ブジェクトを使って、2種類の価格エンジンを作成(567~573行目)
一つ目のエンジンはGaussian1dSwaptionEngineクラスのオブジェクト。これは、CalibrationHelperにセットし、ベンチマークとなるヨーロピアン・スワップションの価格評価に使う。
二つ目のエンジンは、Gaussian1dFloatFloatSwaptionEngineクラスのオブジェクトで、CMSスワップションの価格評価に使う。このクラスは、BasketGeneratingEngine クラスの派生クラスです。(Appendix-1)
(3) 上記の2つ目のエンジンを、既に作成済の CMS スワップションオブジェクトに設定(575行目)
(4) CMS スワップションの価格を、NPV()関数を使って計算(578行目)
計算結果は、コンソール画面出力にある通り、35.49bpとなりました。 GSRモデルでは、42.91bpだったので、20%程度の開きがあります。
(5) CMS スワップションの対象資産である、CMS スワップそのものの価格評価(594~595行目)
これは、CMSスワップションの商品オブジェクトから、result
(6) MFM モデルの Volatilityの期間方向へのCalibrationを行い、その結果を画面出力(614~621行目)
MarkovFunctionalクラスは、CalibratedModelクラスの派生クラスにもなっており、そこでcalibrate()関数をオーバーライドして書き換え、MFM独自のCalibrationアルゴリズムを実装しています。そのアルゴリズムは非常に複雑で、計算に相当程度の時間がかかります。具体的にどのような操作が為されているかは、上級編マルコフ汎関数モデルのセクションを参照して下さい。
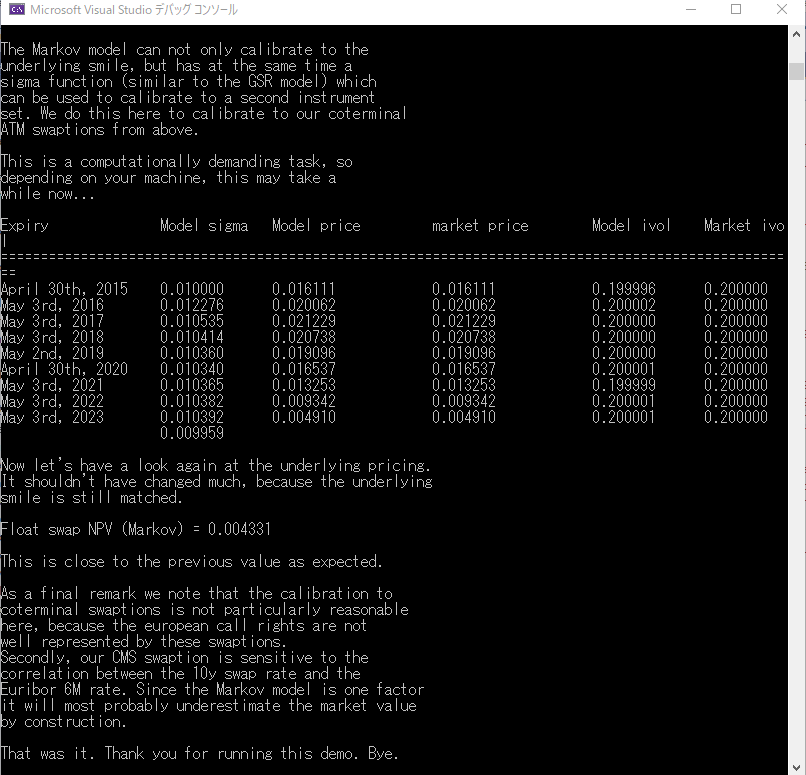
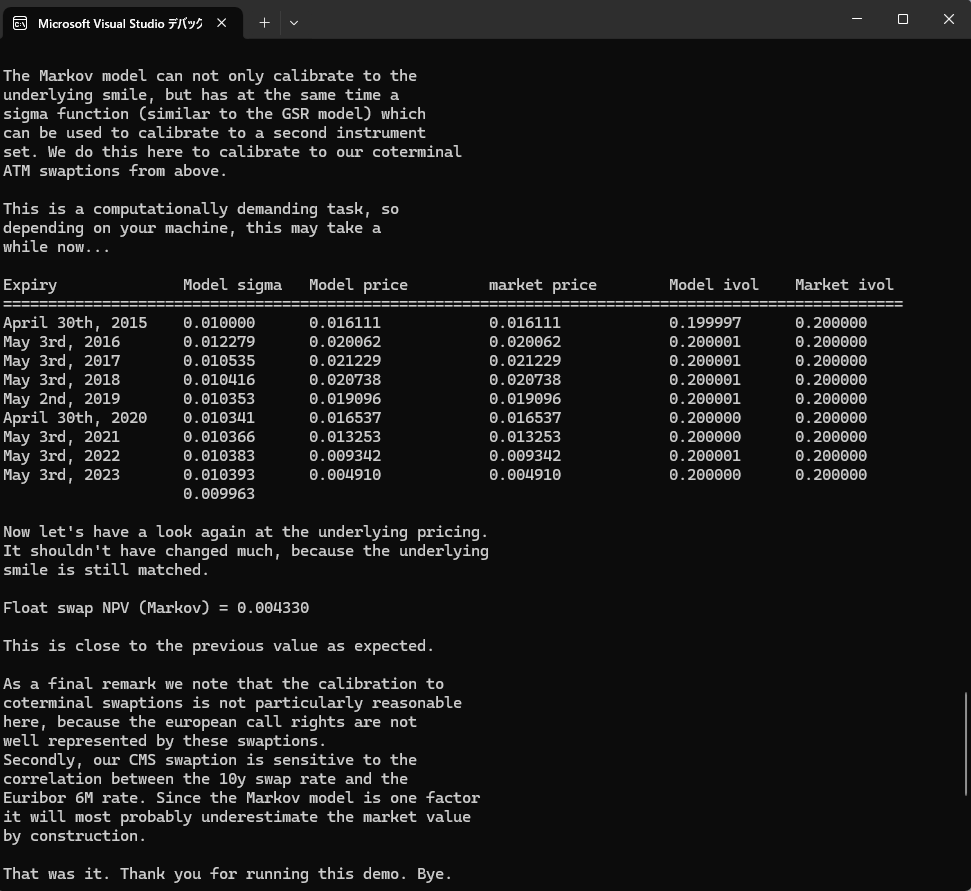
(7) (6),で MFM のVolatilityパラメータを Calibrationした後、CMSの価格評価を行う(629~632行目)
MFMを使ったCMSの価格およびCMSスワップション価格の計算結果は、Console画面出力に出ています。GSRモデルおよびLinear TSRモデルでの計算結果と比較してみて下さい。
以上
Appendix - 1 : BasketGeneratingEngine クラスと NonStandardSwaptionクラス
このプログラム例(Gaussian1dModelsプロジェクト)では、BasketGeneratingEngine クラスと NonStandardSwaption クラスのオブジェクトが随所で使われています。というか、この2つのクラスに備わった calibrationBasket() 関数の使い方をテストするのが、このプログラム例の主な目的になっています。
BasketGeneratingEngine クラスは、QuantLib ライブラリの中では、少し特殊な位置にあります。このクラスは、あまり汎用性が無く、むしろ個別の目的で QuantLib をカスタマイズして作られたクラスのように見受けられます。クラス階層を見てみると、このクラスの親クラスは存在せず、このクラス自体が親クラスになっています。また、ここから派生するクラスは、Gaussian1dFloatFloatSwaptionEngine と Gaussian1dNonstandardSwaptionEngine の2種類のみです。さらに、このクラスで定義されている関数の中に、パラメータがハードコードされている部分があり、汎用性を失わせるような作られ方がしています。
そういった事もあり、このBasketGeneratingEngineクラスは、QuantLibのReference Manualにも載っていません。(GitHubにある、技術者用のReference Manualには載っているので、参考の為にそのURLを添付します。BasketGeneratingEngine Class reference on Github
ただ、このクラスの2種類の派生クラスは、親クラスとしてBasketGeneratingEngineクラスのみならず、GenericModelEngine< Y>テンプレートクラス、さらにその何層か上のベースクラスとして PricingEngine クラスから派生しているので、QuantLib の PricingEngine クラスが提供している様々な機能を使う事が出来ます。参考の為に、BasketGeneratingEngine クラスとその派生クラスのクラス階層構造のチャートを下記します。
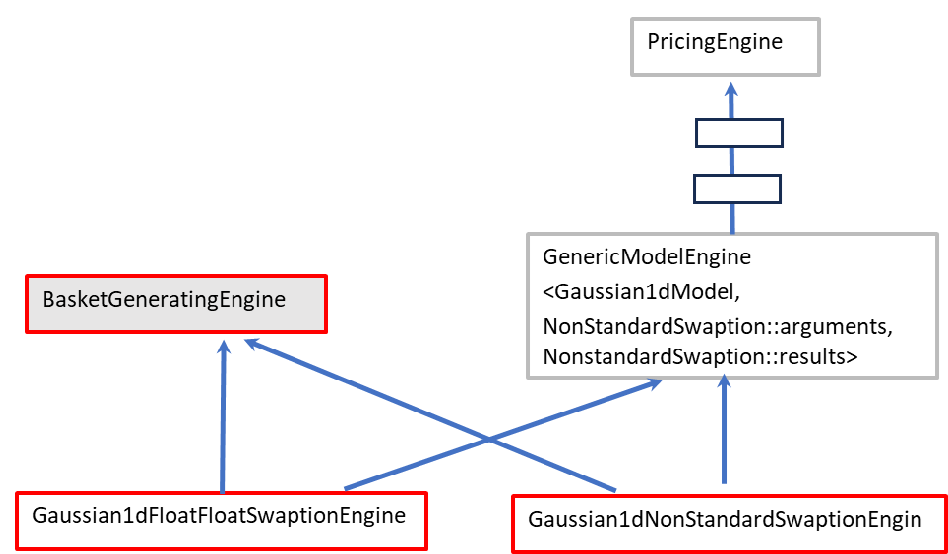
さて、BasketGeneratingEngine クラスが作られた目的は、クラス名からも推察できる通り、CalibrationHelperのBasket(配列)を Generating(自動生成)する機能を持たせる為です。その機能は、このクラスで定義されたcalibrationBasket()関数に実装されています。この関数の機能については、次のAppendix -2 で解説しますが、簡単に言うと、価格評価対象となる商品オブジェクトの特性に合わせたCalibrationHelperを生成する事です。従って、この関数を走らせる為には、価格評価の対象となる商品オブジェクトの情報が必要になります。なので、この関数は価格エンジンから直接呼び出すのではなく、一旦、価格評価の対象となる商品オブジェクトから間接的に呼び出され、その際に商品オブジェクトの情報がこの関数に渡されます。商品オブジェクト側で、この関数を呼び出す関数が、NonStandardSwaptionクラスで定義されている同名のcalibrationBasket()関数です。
NonStandardSwaption クラスは、すべての商品クラスのベースクラスとなる Instrument クラスから派生しています。なので、一応 QuantLib の体系に組み込まれていますが、実際には、BasketGeneratingEngine クラスの calibrationBasket()関数を機能させる為に作られた特別なクラスのように見受けられます。
Appendix - 2: calibrationBasket( ) 関数
プログラム例で何度も登場するこの関数は、NonStandardSwaptionクラスに備わったメンバー関数です。このプログラム例全体で、バーミューダン・スワップションの商品オブジェクトからこの関数が何度も呼び出されています。但し、本文中で説明した通り、この関数の実装(QuantLibライブラリの中の、nonstandardswaption.cppに記述されています)を見ると、この関数からさらに、BasketGeneratingEngine クラスにある同名のメンバー関数を呼び出しており、具体的なアルゴリズムはそこで実装されています。
この関数の役割は、ベンチマークとなるスワップションのVolatility surface(オプション期間軸とストライク軸の2次元データ)を使って、価格評価対象のスワップションと価格エンジンに対応した CalibrationHelper(の派生クラスのSwaptionHelper)の配列を自動生成する事です。その生成方法は下記の2通り用意されています。
1. Naïve : At the moneyのSwaptionHelperの配列を生成
2. MaturityStrikeByDeltaGamma :価格評価の対象となるスワップションのオプション期間、ストライク価格にデルタやガンマがマッチするような SwaptionHelper の配列を生成
これまで見てきた、CallableBondsとBarmudanSwaptionのプロジェクトでは、Short Rate ModelのパラメータをCalibrationする為に、CalibrationHelperを別途、外生的に生成していました。ところが、CalibrationHelperを生成する手順は、実務では簡単ではありません。価格評価の対象となる商品(SwaptionやCap/Floorなど)のストライクによって、ベンチマーク商品のどのストライクのデータを使ってCalibrationを行うかは、簡単な判断ではないからです。特に商品がバーミューダン・スワップションの場合、複数の行使日でそれぞれAt the Moneyとなるスワップレートが異なる為、オプション行使日ごとにベンチマーク商品の適切なストライク金利を探す必要があります。ベンチマーク商品のVolatility曲面では、ストライク軸に沿ってVolatility SmileやVolatility Skewが観測されるので、ATM(At The Money)のデータにCalibrationするのと、OTM/ITMのデータにCalibrationするのでは、結果が大きく異なってきます。
そこで、評価対象のスワップションのオプション期日やストライクに適合したCalibrationHelperを自動的に生成する機能を持たせたのが、この関数になります。
Appendix - 3 : Linear TSR Model と LinearTsrPricer クラス
Linear TSRモデルは、簡単に説明すると
・Terminal Swap Rateとは、オプションの最終期日(Terminal Date)における、対象スワップ金利を意味します。ヨーロピアン・スワップションでは、そのスワップ金利と、スワップションのストライク金利を比較し、スワップションを行使するかどうかの判断をします。
・ 仮にオプション行使した場合、どの程度の損益が発生するかは、その時のスワップ金利だけでは計算できず、その時点のイールドカーブ(金利の期間構造)の情報が必要になります。
・ しかし、Blackモデルなどのシンプルな金利モデルでは、行使日におけるスワップ金利の情報しか得られず、イールドカーブの情報を持っていません。
・ そこで、オプション最終期日のスワップ金利(Terminal Swap Rate)の情報から、何等かの方法で、無理やりイールドカーブを描いてしまおうというのが、Terminal Swap Rate(TSR) Modelになります。
・ その何等かの方法として、いくつか提案されていますが、そのひとつがLinear TSRモデルになります。ゼロクーポン債のニュメレールとの相対価格が、スワップ金利の1次関数で表せると看做すので、こう呼ばれています。
・ 特に、Linear TSRモデルでは、イールドカーブを描く為の情報として、Short Rate Modelの中心回帰強度を使う方法があります。このプログラム例でも、486行目で、中心回帰強度の情報を取得し、それをLinearTsrPricerオブジェクトの部品として使用しています。
以上の簡易な説明では、よく分からないと思いますので、詳細は、Andersen-Piterbargの“Interest Rate Modeling Volume III”のセクション16.3~16.6を参照して下さい。
LinearTsrPricer は、このLinear TSRモデルを使ったCouponPricerで、FloatingRateCouponPricer クラスの派生クラスになります。 FloatingRateCouponPricer については、既に Bonds プロジェクトの中の Appendix-5で解説済みです。再度説明すると、IBOR-CF や CMS-CF などの変動金利キャッシュフローには、しばしばオプション性のある条件が付されたり、コンベクシティ調整が必要であったりします。その為、クーポン毎にモデルを使った価格計算をするので、それぞれのクーポンに価格エンジンを設定します。その価格エンジンの簡易版のようなものが、この FloatingRateCouponPricer クラスになります。
下記に、QuantLibで用意されているFloatingRateCouponPricerクラスのクラス階層を載せます(QuantLibのReference Manualから抜粋)。各クラスの役割は、クラス名からある程度推察できると思いますが、CMS スワップのキャッシュフロー用や、Cap/Floorが付されたIBORにリンクする変動金利CF用のCouponPricerが用意されています。
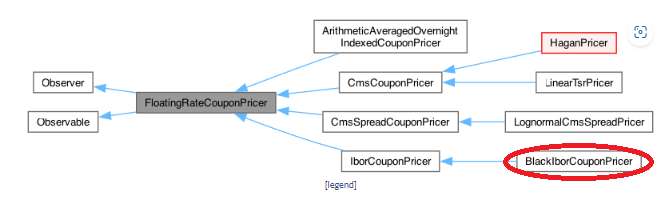
このプロジェクト例では、CMSのCF用として、LinearTsrPricerと、IBORにリンクする変動金利CF用として、BlackIborCouponPricerをそれぞれ使っています。
<ライセンス表示>
QuantLibのソースコードを使う場合は、ライセンス表示とDisclaimerの表示が義務付けられているので、添付します。 ライセンス